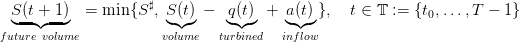
Abstract
We consider a dam manager intenting to maximize the intertemporal payoff obtained by selling hydropower produced by water releases, when the water inflows (rain, outflows from upper dams) and the energy prices are supposed to be deterministic. You will propose different water turbined policies and you will compute their payoff. Then, you will compute the optimal payoff and display the optimal policy. At last, you will evaluate the cost of introducing a “tourism” constraint consisting in having a guaranteed stock volume in the dam during Summer months.
We consider a dam manager intenting to maximize the intertemporal payoff obtained by selling hydropower produced by water releases, when the water inflows (rain, outflows from upper dams) and the energy prices are supposed to be deterministic.
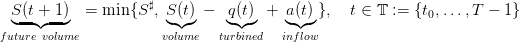 | (1) |
with
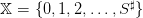 , made of water volumes (h m3), where
, made of water volumes (h m3), where 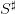 is the
maximum dam volume;
is the
maximum dam volume;
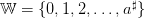 ,
supposed to be deterministic, hence known in advance at initial time t0;
,
supposed to be deterministic, hence known in advance at initial time t0;
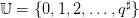 , where q♯ is the maximum which can be
turbined by time unit (and produce electricity), and such that
, where q♯ is the maximum which can be
turbined by time unit (and produce electricity), and such that
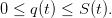 | (2) |
A scenario of water inputs
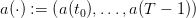 | (3) |
is given (data of the problem), hence known in advance at initial time t0 where the following optimization problem is posed.
The manager original problem is one of payoff maximization where turbining one unit of water has unitary price p(t). On the period from t0 to T, the payoffs sum up to
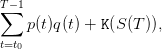 | (4) |
where
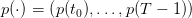 | (5) |
is given (data of the problem) and supposed to be known in advance at initial time t0 where the optimization problem is posed (deterministic setting);
 S(T)
S(T)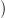 is called the final value of water, since it values the water
volume S(T) in the dam at the horizon T.
is called the final value of water, since it values the water
volume S(T) in the dam at the horizon T.
Time. We consider a daily management (the interval [t,t + 1[ represents one day) over one year
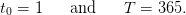 | (6) |
Bounds. Concerning the dam and water inflows, we consider the following bounds:
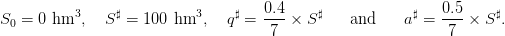 | (7) |
These figures reflect the assumptions that, during one week, one can release at maximum 40% of the dam volume, and that during one week of full water inflows, an empty dam can be half-filled.
Prices scenario.
The scenario  of prices is known in advance. We produce it by one
sample from the expression
of prices is known in advance. We produce it by one
sample from the expression
 | (8) |
where  is drawn from a sequence of i.i.d. uniform random variables in
is drawn from a sequence of i.i.d. uniform random variables in ![[− 0.1,0.1]](dam16x.png) . The
above expression reflects the assumption that prices are seasonal (high in winter for house heating,
and low in summer).
. The
above expression reflects the assumption that prices are seasonal (high in winter for house heating,
and low in summer).
Water inflows scenario.
The scenario  of water inflows is known in advance. We produce it
by one sample from the expression
of water inflows is known in advance. We produce it
by one sample from the expression
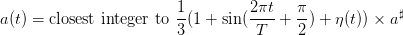 | (9) |
where 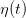 is drawn from a sequence of i.i.d. uniform random variables in
is drawn from a sequence of i.i.d. uniform random variables in ![[0, 1]](dam20x.png) . The above
expression reflects the assumption that water inflows are seasonal (high in winter and low in
summer).
. The above
expression reflects the assumption that water inflows are seasonal (high in winter and low in
summer).
Copy the following Scicoslab code into a file DamData.sce. Check that it indeed corresponds to the data above.
First, we detail how a water turbined policy yields state (stock volume) and control (turbined) trajectories by the dynamics (1), that are then evaluated with the criterion (4). Second, you will propose different policies and you will compute their payoff.
An admissible policy γ : 𝕋 × 𝕏 → 𝕌 assigns a water turbined 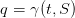 to any state S of dam
stock volume and to any decision period t ∈ 𝕋, while respecting the constraints
to any state S of dam
stock volume and to any decision period t ∈ 𝕋, while respecting the constraints
 | (10) |
that is,
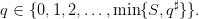 | (11) |
Once given, we obtain a volume trajectory 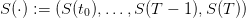 and a turbined
trajectory
and a turbined
trajectory 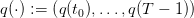 produced by the “closed-loop” dynamics
produced by the “closed-loop” dynamics
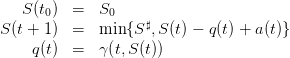 | (12) |
and function of the scenario a(⋅) of water inputs in (3). Thus, in the end, we obtain the payoff
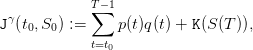 | (13) |
as a function of the policy γ, where the trajectories 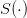 and
and 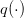 are given by (12).
are given by (12).
Copy the following Scicoslab code into the file DamData.sce. Check that it indeed corresponds
to the expressions (12) and (13) in the special case where the final gain 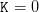 .
.
Load the file DamData.sce by the instruction
Copy the following Scicoslab code into a new file DamOptimality.sce. The code allows you to answer to Question 1.
Question 1
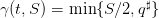 — which turbines half of the stock, except if it is higher
than the capacity q♯ — and evaluate the payoff as in (4).
— which turbines half of the stock, except if it is higher
than the capacity q♯ — and evaluate the payoff as in (4).
Now, you will design new policies, writing code as below, following the example of the half_policy policy.
Question 2
 at initial time t0. What is the best policy among them?
at initial time t0. What is the best policy among them?
As a step towards computing an optimal water turbined policy, we provide the dynamic programming (or Bellman) equation associated with the problem of maximizing the payoff (13), as well as the corresponding Scicoslab code.
The dynamic programming equation associated with the problem of maximizing the payoff (13) is
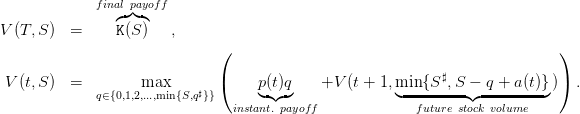 | (14) |
Recall the definition of the characteristic function χA of a set A: χA(q) = 0 if q ∈ A, χA(q) = +∞
if q ⁄∈ A. Getting rid of the constraint 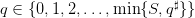 by incorporating it in the
corresponding characteristic function, the dynamic programming equation above can be written
under the equivalent form
by incorporating it in the
corresponding characteristic function, the dynamic programming equation above can be written
under the equivalent form
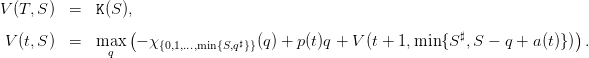 | (15) |
This trick will be used in the Scicoslab code. We will replace the characteristic function χA by a penalization: A(q) = 0 if q ∈ A, A(q) = 1∕𝜖 if q ⁄∈ A, where 𝜖 is a very small positive number.
Copy the following Scicoslab code into the file DamOptimality.sce. Check that it indeed corresponds to the Bellman equation (15).
First, we will go on using a zero final value of water, meaning that leaving a stock in the dam at the end of the year is not valued. Thanks to the Scicoslab code for the Bellman equation (15), you will compute the optimal payoff and compare it with the payoffs obtained in the previous questions. Second, we will display a procedure to give proper value to a final stock. You will then compute the optimal policy and study it. At last, you will examine if this policy, designed for a single specific water inflows scenario, is sensitive to a change of scenario (robustness).
We first consider that the final “value of water” is zero:
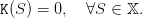 | (16) |
Copy the following Scicoslab code into the file DamOptimality.sce.
Question 3
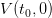 evaluated at initial
time t0 and initial empty stock
evaluated at initial
time t0 and initial empty stock 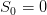 ?
?
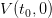 by definition.
by definition.
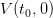 .
.
Till now, there was no gain in leaving water in the dam at the ultimate decision period as reflected
in (16). Now, we consider that the final gain 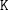 is non zero, and we provide a procedure to
estimate a “final value of water”, that is, a function S
is non zero, and we provide a procedure to
estimate a “final value of water”, that is, a function S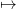 K(S) as in (4).
K(S) as in (4).
The intuition behind the procedure is that the final value of water is the value that a manager would put on the dam, were he to run it from the date T + 1 to infinity. The final value of water is the solution of an infinite horizon maximization problem. The procedure below mimicks an algorithm to find a fixed point by iterations.
First, we start with a zero final value of water 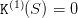 and obtain, by backward
induction, the Bellman function
and obtain, by backward
induction, the Bellman function 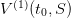 at initial time. Up to a translation — to account for
the fact that an empty dam has zero final value of water — we identify
at initial time. Up to a translation — to account for
the fact that an empty dam has zero final value of water — we identify 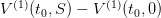 with the new final value of water
with the new final value of water 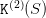 . Proceeding along, we expect that this loop
converges towards a function S
. Proceeding along, we expect that this loop
converges towards a function S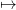 K(∞)(S) which is a good candidate for the final value of
water.
K(∞)(S) which is a good candidate for the final value of
water.
We design a loop for k = 1,…,K, starting with a zero final value of water
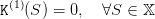 | (17) |
then solving the backward Bellman equation
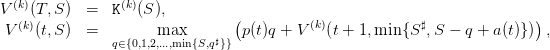 | (18) |
then closing the loop by choosing the new final value of water
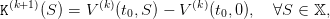 | (19) |
as the Bellman function at the initial time t0 after translation, so that 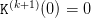 .
.
Copy the following Scicoslab code into the file DamOptimality.sce.
Question 4
Copy the following Scicoslab code into the file DamOptimality.sce.
Question 5
 q = γ⋆(t,S) for some values of time t, where γ⋆ is the optimal policy
numerically found (use plot2d2). Comment on their forms and on the structure of
optimal policies.
q = γ⋆(t,S) for some values of time t, where γ⋆ is the optimal policy
numerically found (use plot2d2). Comment on their forms and on the structure of
optimal policies.
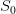 . Give the values
of the Bellman function
. Give the values
of the Bellman function 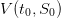 evaluated at initial time t0 and the same values of
the initial stock
evaluated at initial time t0 and the same values of
the initial stock 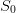 . Write them all in a table and compare them.
. Write them all in a table and compare them.
The optimal policy discussed in Question 5 is taylored for one single inflows scenario. We now want to figure out how it responds to other inflows scenarios.
Question 6
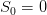 ), with the optimal policy of Question 5. Picture the histogram of the
250 payoffs.
), with the optimal policy of Question 5. Picture the histogram of the
250 payoffs.
For “tourism” reasons, the following viability constraint is imposed on the stock volume during some Summer months:
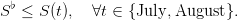 | (20) |
Such a state constraint can be treated by dynamic programming by incorporating it in the corresponding characteristic function.
Question 7
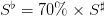 .
.
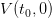 evaluated
at the initial time t0 and the initial stock
evaluated
at the initial time t0 and the initial stock 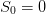 .
.
The viability constraint (20) is an additional constraint, hence reduces the domain of optimization. Therefore, the payoff is lower.
Question 8 For 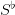 varying regularly between 0% to 100% of
varying regularly between 0% to 100% of 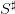 , compute the “cost of
the viability constraint”, as the difference between the optimal payoff without and with the
“tourism” viability constraint.
, compute the “cost of
the viability constraint”, as the difference between the optimal payoff without and with the
“tourism” viability constraint.