Contents
1 Optimal Allocation in Random Environment (Theory)
1.1 Optimisation model in random environment
We extend the model in constant environment introduced at Optimal Resources Allocation in
Ecology: to Grow or to Reproduce? (I) to a random environment as follows. We suppose that
- the total biomass generated during one period is now a function of environmental state
R; thus, x
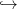 f(x) is now replaced by a function x
f(x) is now replaced by a function x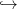 f(x,R) with the same properties;
f(x,R) with the same properties;
- the environmental state Rt occurs during period [t,t+1[; we assume that it is a random
variable having values in a finite set {r1,...,rm};
- the random variables sequence R0,...,RT−1 forms a homogeneous Markov chain; we
denote by π the matrix of general term π(i,j) = ℙ(Rt+1 = rj|R
t = ri);
- at the beginning of period [t,t + 1[, the realization of the random variable Rt is
experienced by the plant.
Stochastic dynamics
The stochastic dynamics of the plant is the following. Consider a plant starting at the beginning of
period [t,t + 1[ with vegetative biomass x ∈ ℝ+ and subject to environmental state ri. Applying
the control v ∈ [0, 1], at the end of period [t,t + 1[, the plant
- either dies, i.e. transits towards vegetative biomass 0, with probability 1 − β ;
- transits towards vegetative biomass vf(x,rj) with probability βπ(i,j).
In parallel, the environmental state ri transits towards state rj with probability π(i,j).
Control
The control v is here the fraction of total biomass allocated to growth.
Now, a (Markovian) strategy v() is a mapping {0,...,T − 1}× ℝ+ ×{r1,...,rm}→ [0, 1]:
v0,...,vT−1 are in feedback on both vegetative biomass and on environmental state.
Feedback strategies
An optimal strategy for the plant is a strategy which maximizes the mathematical expectation
of the fitness, here the cumulated offspring (reproductive biomass) at the end of the
season:
![T∑−1
J(v(.)) = 𝔼( (1 − vt)f(xt,Rt)) with v(.) = (v0,...,vT−1) ∈ [0,1]T .
t=0](english_Plant_alloc_II2x.png) | (1) |
Since the environmental states have values in the finite set {r1,...,rm}, and since mortality may be
modeled by a random variable with values in {0, 1}, the expectation is here a finite
sum.
1.2 Resolution by stochastic dynamic programming
The stochastic dynamic programming equation (sdpe) is
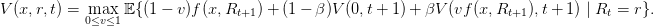 | (2) |
Question 1 Show by induction that V (0,t) = 0, so that
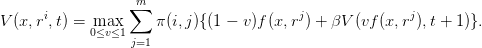 | (3) |
2 Computation of optimal strategies in random environment (PW Scilab)
We take
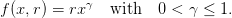 | (4) |
The reader has less informations than in the constant environment case. However, the Scilab code
includes many comments.
2.1 Discretization of the problem
In this model, contrarily to the constant environment case, the state is no longer the single
vegetative biomass x, but is the couple (x,R) ∈ ℝ+ ×{r1,...,rm}.
First, we discretize the space ℝ+ in {x1,...,xn}, where x1 corresponds to x = 0 (dead plant)
and xn is a maximal vegetative biomass for the plant. We also discretize the function
(x,r,v)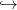 vf(x,r) in a function
vf(x,r) in a function
![F : {x1, ...,xn } × {r1,...,rm} × [0,1] → {x1, ...,xn }.](english_Plant_alloc_II7x.png) | (5) |
Then, we express the stochastic dynamics above by a family, indexed by the controls v, of
transition probabilities Mv on the finite product set {x1,...,xn}×{r1,...,rm}.
2.2 Using hypermatrices
Since the state is two dimensional, after discretization it becomes a couple in a finite
product set. Thus, transition probabilities are not naturally matrices, but are rather
hypermatrices.
The following Scilab code expresses these transition probabilities Mv by means of four
indexes hypermatrices. An hypermatrix is an extension with more than two indexes of
Scilabmatrices.
The vector taille has for elements the sequence (x1,...,xm) of values taken by discretized
biomass: taille(i) = xi, i = 1,...,m.
2.2.1 Environmental states transitions
The vector env has for elements the sequence (r1,...,rm) of values taken by the environment:
env(i) = ri, i = 1,...,m.
Open a new file plantII.sci and copy the following code. It provides different examples of
transition matrices π for the environment Markov chain.
function pi=tr_env_auc_cor_unif(cardinal_alea)
dd=cardinal_alea
pi=1/dd*ones(dd,dd) endfunction function pi=tr_env_cor_proche_vois(cardinal_alea)
dd=cardinal_alea
pi=diag([0.5,1/3*ones(1:(dd-2)),0.5])+diag([0.5,1/3*ones(1:(dd-2))],1)+ ...
diag([1/3*ones(1:(dd-2)),0.5],-1) endfunction function pi=tr_env_cor_crois(cardinal_alea,rho)
dd=cardinal_alea pi=diag([rho*ones(1:(dd-1)),1])+diag([(1-rho)*ones(1:(dd-1))],1)
endfunction function pi=tr_env_cor_decrois(cardinal_alea,rho)
dd=cardinal_alea pi=diag([1,rho*ones(1:(dd-1))])+diag([(1-rho)*ones(1:(dd-1))],-1)
endfunction function pi=tr_env_cor_et_chute(cardinal_alea,rho)
dd=cardinal_alea pi=diag([rho*ones(1:dd)]) pi(2:$,1)=1-rho pi(1,2)=1-rho
endfunction function pi=tr_env_cor_et_ascension(cardinal_alea,rho)
dd=cardinal_alea pi=diag([rho*ones(1:dd)]) pi(1:$,$)=1-rho pi(dd,dd-1)=1-rho endfunction
2.2.2 State transitions
In the file plantII.sci, copy the following code which encapsulates both state and environment
transitions in the so called Scilab object hypermatrices.
function Hypermatrices=constr_HyperM(taille,env,control,pi,controlled_dynamics)
dims=[prod(size(taille)),prod(size(env))]; ddims=[dims(1),dims(1),dims(2),dims(2)];
Hypermatrices=list(); cardinal_control=prod(size(control));
cardinal_taille=prod(size(taille)); for l=1:cardinal_control do
Hypermat=hypermat([ddims]);
for y=1:dims(2) do image=controlled_dynamics(taille,y,control(l));
indexes_image_discretisee=predec_succes(taille,image);
indexes1=indexes_image_discretisee(1); indexes2=indexes_image_discretisee(2);
probabilites=indexes_image_discretisee(3); M1=zeros(cardinal_taille,cardinal_taille);
M2=zeros(M1); for i=1:cardinal_taille do
M1(i,indexes1(i))=probabilites(i); M1(i,indexes2(i))=1-probabilites(i);
end for z=1:dims(2) do Hypermat(:,1,y,z)=(1-ateb)*pi(y,z);
Hypermat(:,:,y,z)=Hypermat(:,:,y,z)+(M1+M2)*ateb*pi(y,z); end
end
Hypermatrices(l)=Hypermat end endfunction
2.3 Conversion operations to fit with the Scilab function Bell_stoch
The Scilab function Bell_stoch allows numerical resolution of the stochastic dynamic
programming equation. It is written for a Markov chain on {1,2...,taille_state}. Indeed, the
algorithm is powerful because state is identified with a vector index.
This is why, the four indexes transition hypermatrices will be transformed into ordinary
matrices with two indexes by “unrolling” the indexes. For instance, the following matrix
(particular case of hypermatrix) 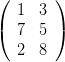 will be unrolled in (1, 7, 2, 3, 5, 8).
will be unrolled in (1, 7, 2, 3, 5, 8).
This is how to a couple (x,r) ∈{x1,...,xn}×{r1,...,rm} we associate a state e ∈{1,...,n×m}.
We numerically solve the optimization problem with this state space (intermediary and
one-dimensional). Then, we go back to the original two-dimensional state space.
In the file plantII.sci, copy the following code in which conversion Scilab macros are
defined.
function Matrices=conv_HyperM(Hypermatrices)
dd=size(Hypermatrices(1)) dims=[dd(1),dd(3)]
Matrices=list() for i=1:prod(size(control)) do
Mat=[] for j=1:dims(2) do if dims(2) <> 1 then
a=Hypermatrices(i)(:,:,j,:).entries b=matrix(a,dims(1),prod(dims))
else b=matrix(Hypermatrices(i)(:,:,j,:),dims(1),prod(dims)) end
Mat=[Mat;b]
end
Matrices(i)=full(Mat) end endfunction function n=convert1(i,j,dims)
if i > dims(1) | j > dims(2) then n='i ou j > dims' else
n=(j-1)*dims(1)+i; end endfunction function [i,j]=convert2(n,dims)
i=modulo(n,dims(1))
ind=find(i==0) i(ind)=dims(1) j=int(n/dims(1))+1 ind2=find((dims(1))\n==int((dims(1))\n))
jj=(dims(1))\n j(ind2)=jj(ind2) endfunction function Hmat=convert2_mat(matrix,dims)
Hmat=hypermat([dims,T-1]) n=1:prod(dims) [i,j]=convert2(n,dims) for t=1:T-1 do
for index=1:prod(dims) do Hmat(i(index),j(index),t)=matrix(n(index),t) end
end endfunction function instant_cost=conv_cost(taille,env,control,cost,horizon)
dims=[prod(size(taille)),prod(size(env))]
instant_cost=list() for j=1:prod(size(control)) do cost_i=[]
for t=1:horizon do
cost_it=hypermat(dims); for state1=1:dims(1) do for state2=1:dims(2) do
cost_it(state1,state2)=cost(taille(state1),env(state2),control(j),t)
end end cost_it=matrix(cost_it,1,prod(dims))
cost_i=[cost_i(cost_it)']
end instant_cost(j)=full(cost_i) end endfunction
2.4 Transitions and costs adapted to the Scilab function Bell_stoch
Open a file plantII.sce and copy the following code.
exec('plantI2.sci'); exec('plantII.sci'); T=10; ateb=0.9; rr=1.2; power=0.5;
xp=(ateb*rr*power)^{1/(1-power)}; xm=(xp/rr)^{1/power}; taille=[0:(xm/3):(1.2*xp)];
env=[0.6,0.8,1,1.2,1.4]; control=0:0.05:1;
cardinal_env=prod(size(env)); cardinal_taille=prod(size(taille));
pi=tr_env_auc_cor_unif(cardinal_env);
function b=dyn_plant_control(x,r,v)
b=v*r*x^{power} endfunction controlled_dynamics=dyn_plant_control;
Hypermatrices=constr_HyperM(taille,env,control,pi,controlled_dynamics);
transition_matrix=conv_HyperM(Hypermatrices); function ci=offspring2(taille,env,control,time)
ci=(1-control)'*env*taille^(power)*ateb^{time-1}
ind=find(taille==1),ci(ind)=0 endfunction offspring=conv_cost(taille,env,control,offspring2,T);
final_cost_nul=zeros(cardinal_env*cardinal_taille,1);
Question 2 Check that the list of matrices matrix_transition indeed consists of
transition matrices, that is with nonnegative coefficients summing to 1 on each row.
2.5 Simulation of optimal trajectories
Copy the following code in the file plantII.sce.
dims=[cardinal_taille,cardinal_env]; stacksize(3000000); instant_cost=offspring;
final_cost=final_cost_nul; [value,feedback]=Bell_stoch(transition_matrix,instant_cost,final_cost,1);
index_taille_init=grand(1,1,'uin',2,cardinal_taille); index_env_init=grand(1,1,'uin',1,cardinal_env);
initial_state=convert1(index_taille_init,index_env_init,dims);
z=trajopt(transition_matrix,feedback,instant_cost,final_cost,initial_state);
[index_taille,index_env]=convert2(z(1),dims)
x=taille(index_taille); e=env(index_env);
xset("window",1);xbasc();plot2d2(1:prod(size(x)),x); xtitle("taille")
xset("window",2);xbasc();plot2d2(1:prod(size(e)),e,rect = [0,0,T+1,max(e)+1]); xtitle("environment")
xset("window",3);xbasc();plot2d2(1:prod(size(control(z(2)))),control(z(2))); xtitle("control")
xset("window",4);xbasc();plot2d2(1:prod(size(z(3))),z(3)); xtitle("fitness")
Question 3 Execute different simulations. Change the matrix pi in the file plantII.sce.
3 Scilab Code
 f(x) is now replaced by a function x
f(x) is now replaced by a function x f(x,R) with the same properties;
f(x,R) with the same properties;
 f(x) is now replaced by a function x
f(x) is now replaced by a function x f(x,R) with the same properties;
f(x,R) with the same properties;
![T∑−1
J(v(.)) = 𝔼( (1 − vt)f(xt,Rt)) with v(.) = (v0,...,vT−1) ∈ [0,1]T .
t=0](english_Plant_alloc_II2x.png)
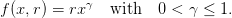
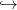 vf(x,r) in a function
vf(x,r) in a function
![F : {x1, ...,xn } × {r1,...,rm} × [0,1] → {x1, ...,xn }.](english_Plant_alloc_II7x.png)
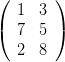 will be unrolled in (1, 7, 2, 3, 5, 8).
will be unrolled in (1, 7, 2, 3, 5, 8).