Programmation dynamique
Macros générales

Michel de lara
(last modification date: October 10, 2017)
Version pdf de ce document
Version sans bandeaux

1 Programmation dynamique stochastique sur des entiers (cas des matrices de transition)
2 Programmation dynamique stochastique sur des entiers (cas dynamique bruitée)
3 Transcription en objets Scilab
4 Macros Scilab pour la résolution numérique (cas des matrices de transition)
5 Macros Scilab pour la résolution numérique (cas dynamique bruitée)
6 Programmation dynamique stochastique sur un ensemble fini
7 Problèmes de discrétisation

Contents

1 Programmation dynamique stochastique sur des entiers (cas des matrices de transition)
2 Programmation dynamique stochastique sur des entiers (cas dynamique bruitée)
3 Transcription en objets Scilab
4 Macros Scilab pour la résolution numérique (cas des matrices de transition)
 4.1 Résolution de l’équation de la programmation dynamique stochastique
 4.2 Simulation de trajectoires optimales
5 Macros Scilab pour la résolution numérique (cas dynamique bruitée)
6 Programmation dynamique stochastique sur un ensemble fini
7 Problèmes de discrétisation
 7.1 Dynamique stochastique commandée
 7.2 Discrétisation d’un problème d’optimisation stochastique sur ℝ
 7.3 Discrétisation d’un problème d’optimisation stochastique sur ℝn
 7.4 Discrétisation d’un problème d’optimisation déterministe sur ℝ et mise sous forme stochastique
 7.5 Discrétisation d’un problème d’optimisation stochastique sur ℝN, N ≥ 2

1 Programmation dynamique stochastique sur des entiers (cas des matrices de transition)

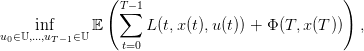
Le problème d’optimisation considéré ici est

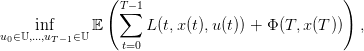(T −1 ) ∑ u0∈𝕌,i..n.,fuT−1∈𝕌𝔼 L(t,x(t),u(t)) + Φ (T, x(T )) , t=0
(1)

avec

  1. coût instantané, L : {0,...,T − 1}×{1,...,n}×{1,...,p}→ ℝ, où
    1. n ∈ ℕ∗ est le cardinal de l’espace d’état 𝕏 := {1,...,n}⊂ ℕ∗,
    2. p ∈ ℕ∗ est le cardinal de l’espace de commande 𝕌 := {1,...,p}⊂ ℕ∗,
    3. T ∈ ℕ∗ est l’horizon,
  2. coût final, Φ : {1,...,n}→ ℝ,
  3. matrices de transition, M : {1,...,p}→ℳ(n,n), application à valeurs dans les matrices (n,n) stochastiques, c’est-à-dire ∀u = 1,...,p,
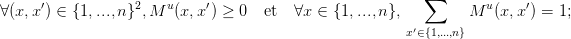
    ′ 2 u ′ ∑ u ′ ∀(x, x) ∈ {1,...,n } ,M (x,x ) ≥ 0 et ∀x ∈ {1,...,n}, M (x,x ) = 1; x′∈{1,...,n}

    le terme Mu(x,x′) représente la probabilité que, partant de l’état x et appliquant la commande u à l’instant t, le futur état au temps t + 1 soit x′ :

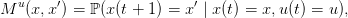
    M u(x,x′) = ℙ(x(t + 1) = x′ | x (t) = x,u (t) = u ),

  4. fonction valeur
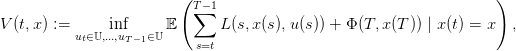    (T − 1 ) ∑ V (t,x) := ut∈𝕌,.in..f,uT−1∈𝕌𝔼 L(s,x (s),u (s )) + Φ (T, x(T )) | x (t) = x , s=t
    		(2)

    la fonction valeur évaluée sur l’état x à l’instant t,

  5. l’équation de la programmation dynamique
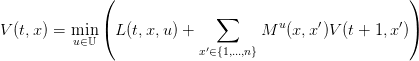    ( ) ( ∑ u ′ ′) V (t,x) = mui∈n𝕌 L(t,x,u ) + M (x,x )V (t + 1,x ) x′∈{1,...,n}
    		(3)

  6. feedback optimal
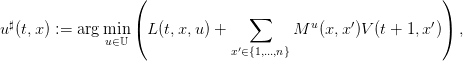    ( ) ∑ u ♯(t,x) := argmin (L (t,x,u) + M u(x,x′)V(t + 1,x′)) , u∈𝕌 x′∈{1,...,n}
    		(4)

    si l’inf est atteint en un unique argument,

  7. trajectoires d’état, de commande, de coût
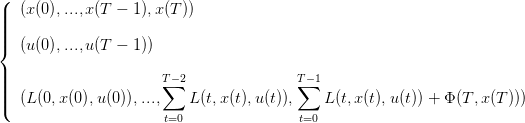    ( || (x(0),...,x(T − 1),x(T)) ||| |{ (u(0),...,u(T − 1)) ||| T∑−2 T∑− 1 |||( (L (0,x(0),u(0)),..., L (t,x(t),u (t)), L(t,x(t),u(t)) + Φ (T,x(T ))) t=0 t=0
    		(5)

2 Programmation dynamique stochastique sur des entiers (cas dynamique bruitée)

Le problème d’optimisation considéré ici identique avec

  1. coût instantané,
  2. coût final
  3. dynamique bruitée, F : {0,...,T − 1}×{1,...,n}×{1,...,p}× 𝕎 →{1,...,n}, application telle que
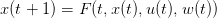    x (t + 1) = F (t,x (t),u (t),w (t))
    		(6)

    où w(0),…,w(T − 1) est une suite de variables aléatoires i.i.d.

  4. fonction valeur
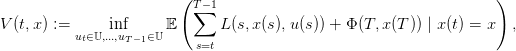    ( ) T∑− 1 V (t,x) := inf 𝔼 L(s,x (s),u (s )) + Φ (T, x(T )) | x (t) = x , ut∈𝕌,...,uT−1∈𝕌 s=t
    		(7)

    la fonction valeur évaluée sur l’état x à l’instant t, prise sur une loi produit ℙ sur 𝕎T ;

  5. l’équation de la programmation dynamique
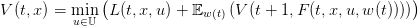    ( ) V (t,x) = mui∈n𝕌 L (t,x, u) + 𝔼w(t) (V (t + 1,F (t,x, u,w(t))))
    		(8)

  6. feedback optimal
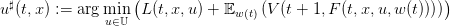    ♯ ( ) u (t,x) := argmui∈n𝕌 L (t,x,u) + 𝔼w(t)(V(t + 1,F (t,x, u,w (t))))
    		(9)

    si l’inf est atteint en un unique argument,

  7. trajectoires d’état, de commande, de coût

3 Transcription en objets Scilab

  1. Le coût instantané est une liste cout_instantane à p éléments composée de matrices de dimension (n,T) :
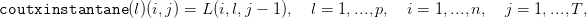    coutxinstantane (l)(i,j) = L(i,l,j − 1), l = 1,...,p, i = 1,...,n, j = 1,...,T ,
    		(10)

    où on notera le décalage dans les indices temporels, et où

    1. le cardinal n de l’espace d’état est un entier cardinal_etat
      cardinalxetat = size (coutxinstantane (1)) (1) = n,
      		(11)

    2. le cardinal p de l’espace de commande est un entier
      cardinalxcommande = size(coutxinstantane ) = p,
      		(12)

    3. l’horizon T est un entier horizon
      horizon = 1 + size (coutxinstantane (1) )(2) = T
      		(13)

  2. le coût final est un vecteur cout_final de dimension (n, 1) :
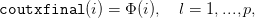    coutxfinal (i) = Φ(i), l = 1,...,p,
    		(14)

  3. Transitions
    1. les matrices de transition sont une liste mat_transition à p éléments composée de matrices (n,n) stochastiques :
      matxtransition (l)(i,i′) = M l(i,i′), l = 1,...,p, i = 1,...,n, i′ = 1,...,n,
      		(15)

    2. la dynamique bruitée est une fonction dynamique(t,i,l,w)
  4. la fonction valeur est une matrice valeur de dimension (n,T + 1) :
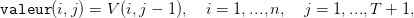    valeur (i,j) = V (i,j − 1), i = 1,...,n, j = 1,...,T + 1,
    		(16)

    où on notera le décalage dans les indices temporels,

  5. le feedback optimal est une matrice feedback de dimension (n,T) :
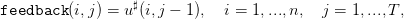    feedback (i,j) = u ♯(i,j − 1), i = 1,...,n, j = 1, ...,T ,
    		(17)

    où on notera le décalage dans les indices temporels,

  6. les trajectoires d’état, de commande, de coût sont des vecteurs trajectoire_etat, trajectoire_commande et trajectoire_cout, de dimensions respectives (1,T + 1), (1,T) et (1,T + 1) :
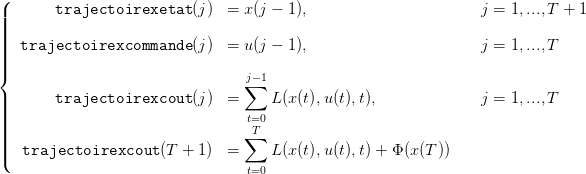    ( || trajectoirexetat (j) = x(j − 1), j = 1,...,T + 1 ||| ||| trajectoirexcommande (j) = u(j − 1), j = 1,...,T |||{ j∑−1 | trajectoirexcout (j) = L (x(t),u(t),t), j = 1,...,T |||| t=0 ||| ∑T ||| trajectoirexcout (T + 1) = L (x(t),u(t),t) + Φ (x (T)) ( t=0
    		(18)

4 Macros Scilab pour la résolution numérique (cas des matrices de transition)

4.1 Résolution de l’équation de la programmation dynamique stochastique

L’astuce employée ici consiste à utiliser un indice dans une matrice pour représenter l’état.

  function [valeur,feedback]=Bell_stoch(matrice_transition,cout_instantane,cout_final, ...
                                        miniOUmaxi)
    // algorithme de programmation dynamique stochastique
    //     pour une chaîne de Markov sur \{1,2...,cardinal_etat\}
    // matrice_transition = liste à cardinal_commande éléments
    //     composée de matrices de dimension (cardinal_etat,cardinal_etat)
    // cout_instantane = liste à cardinal_commande éléments
    //     composée de matrices de dimension (cardinal_etat,horizon-1)
    // cout_final = vecteur de dimension (cardinal_etat,1)
    // valeur = fonction valeur de Bellman,
    //     matrice de dimension (cardinal_etat,horizon)
    // feedback = commande en feedback sur l'état et le temps
    //     matrice de dimension (cardinal_etat,horizon-1)
    // MINIMISATION si miniOUmaxi=-1
    // MAXIMISATION si miniOUmaxi=1
  
    ee=size(cout_instantane(1));cardinal_etat=ee(1);
    cardinal_commande=size(cout_instantane);
    hh=size(cout_instantane(1));horizon=1+hh(2);
  
    valeur=0*ones(cardinal_etat,horizon);
    // tableau ou l'on stocke la fonction de Bellman
    // valeur(:,t) est un vecteur
    // : représente ici le vecteur d'état
  
    valeur(:,horizon)=cout_final;
    // La fonction valeur au temps T est cout_final
  
    feedback=0*ones(cardinal_etat,horizon-1);
    // tableau ou l'on stocke le feedback u(x,t)
  
    // Calcul rétrograde de la fonction de Bellman et
    // de la commande optimale à la date 'temp' par l'équation de Bellman
    // On calcule le coût pour la commande choisie connaissant la valeur de la
    // fonction coût à la date suivante pour l'état obtenu
  
    for temp=horizon:-1:2 do
      // équation rétrograde
      // (attention, pour des questions d'indices, bien finir en :2)
      loc=zeros(cardinal_etat,cardinal_commande);
      // variable locale contenant les valeurs de la fonction à minimiser
      // loc est une matrice
      for j=1:cardinal_commande do
        loc(:,j)=matrice_transition(j)*valeur(:,temp)+cout_instantane(j)(:,temp-1);
      end;
  
      [mmn,jjn]=mini(loc,'c');
      [mmx,jjx]=maxi(loc,'c');
      // mm est l'extremum atteint
      // jj est la commande qui réalise l'extremum
  
      valeur(:,temp-1)=(1-miniOUmaxi)/2*mmn+(1+miniOUmaxi)/2*mmx;
      // mm;
      // coût optimal
      feedback(:,temp-1)=(1-miniOUmaxi)/2*jjn+(1+miniOUmaxi)/2*jjx;
      //jj;
      // feedback optimal 
    end
  endfunction

4.2 Simulation de trajectoires optimales

  function z=trajopt(matrice_transition,feedback,cout_instantane,cout_final,etat_initial)
    // z est une liste :
    // z(1) est la trajectoire optimale obtenue partant de etat_initial
    // z(2) est la trajectoire correspondante des commandes optimales
    // z(3) est la trajectoire correspondante des coûts 
    // etat_initial = un entier 
    // pour le reste, voir la macro Bell_stoch
  
    ee=size(cout_instantane(1));cardinal_etat=ee(1);
    cardinal_commande=size(cout_instantane);
    hh=size(cout_instantane(1));horizon=1+hh(2);
  
    z=list();
    x=etat_initial;
    u=[];
    c=[];
  
    for j=1:horizon-1 do
      // remplissage des trajectoires : commande, coût, état
      u=[u,feedback(x($),j)];
      c=[c,c($)+cout_instantane(u($))(x($),j)];
      mat_trans=full(matrice_transition(u($)));
      x=[x,grand(1,'markov',mat_trans,x($))];
    end
    c=[c,c($)+cout_final(x($))];
  
    z(1)=x;z(2)=u;z(3)=c;
  endfunction

5 Macros Scilab pour la résolution numérique (cas dynamique bruitée)

6 Programmation dynamique stochastique sur un ensemble fini

Le problème d’optimisation est toujours (1), mais avec

  1. coût instantané, L : {x1,...,xn}×{u1,...,up}×{0,...,T}→ ℝ, où
    1. 𝕏 := {x1,...,xn} est l’espace d’état,
    2. 𝕌 := {u1,...,up} est l’espace de commande,
    3. T ∈ ℕ∗ est l’horizon,
  2. coût final, Φ : {x1,...,xn}→ ℝ,
  3. matrices de transition
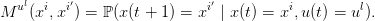    M ul(xi,xi′) = ℙ(x(t + 1) = xi′ | x(t) = xi,u(t) = ul).
    		(19)

On se ramène au cas des entiers en introduisant

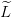  1. nouveau coût instantané, ^L : {1,...,n}×{1,...,p}×{0,...,T − 1}→ ℝ, avec
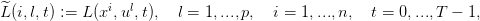    i l ^L (i,l,t) := L (x ,u ,t), l = 1,...,p, i = 1,...,n, t = 0,...,T − 1,
    		(20)

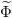  2. nouveau coût final, ^Φ : {1,...,n}→ ℝ, avec
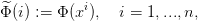    ^Φ(i) := Φ (xi), i = 1,...,n,
    		(21)

  3. transition
    1. nouvelles matrices de transition définies par
      ^M l(i,i′) := M ul(xi,xi′).
      		(22)

    2. dynamique bruitée...

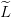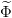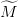On transcrit ces données ^L, ^Φ et ^M en objets Scilab cout_instantane, cout_final, matrice_trans. L’exécution de la macro Bell_stoch retourne en particulier feedback.

Pour la simulation de trajectoires optimales, il suffit alors d’introduire un vecteur etat de dimension (1,n) et tel que

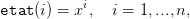etat (i) = xi, i = 1,...,n,
(23)

et un vecteur commande de dimension (1,p) et tel que

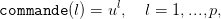commande (l) = ul, l = 1,...,p,
(24)

et d’exécuter une instruction du type

  etat_initial=i;
  // correspond à l'état original x^i
  z=trajopt(matrice_trans,feedback,cout_instantane,cout_final,etat_initial)
  
  zz=list();
  zz(1)=etat(z(1));
  zz(2)=commande(z(2));
  zz(3)=z(3);

7 Problèmes de discrétisation

Les problèmes de discrétisation de l’espace d’état se posent assez naturellement quand le problème d’optimisation n’est pas formulé directement avec des matrices de transition, mais plutôt par le biais d’une fonction de dynamique. C’est ainsi qu’un problème d’optimisation déterministe est généralement formulé, mais aussi de nombreux problèmes d’optimisation stochastique.

7.1 Dynamique stochastique commandée

Une dynamique commandée est une application

F : 𝕏 × 𝕌 → 𝕏.
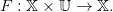(25)

Une dynamique stochastique commandée est une application

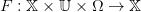F : 𝕏 × 𝕌 × Ω → 𝕏
(26)

où 𝕏 est un espace mesurable, (Ω,μ) est un espace de probabilité, et où F(x,u,⋅) est supposée mesurable pour tous (x,u) ∈ 𝕏 × 𝕌.

Dans le cas où 𝕏 = {x1,...,xn} est un ensemble fini et où

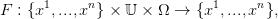F : {x1,...,xn } × 𝕌 × Ω → {x1,...,xn },
(27)

il est immédiat de définir une famille de matrices de transition sur 𝕏 = {x1,...,xn} par

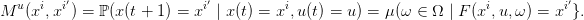M u(xi,xi′) = ℙ (x (t + 1) = xi′ | x (t) = xi,u(t) = u) = μ (ω ∈ Ω | F (xi,u,ω ) = xi′}.
(28)

7.2 Discrétisation d’un problème d’optimisation stochastique sur ℝ

Nous supposons donnée une dynamique stochastique commandée

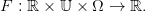F : ℝ × 𝕌 × Ω → ℝ.
(29)

Nous discrétisons l’espace d’état ℝ en {x1,...,xn}, avec x1 < ⋅⋅⋅ < xn. Nous discrétisons également l’espace de commande 𝕌 en {u1,...,ul}.

Nous définissons les applications prédécesseur Π : ℝ →{x1,...,xn} et successeur Σ : ℝ →{x1,...,xn} par

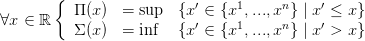{ ′ 1 n ′ ∀x ∈ ℝ Π (x ) = sup {x ′∈ {x1,...,xn} | x ′≤ x } Σ (x ) = inf {x ∈ {x ,...,x } | x > x }
(30)

avec la convention que sup ∅ = x1 et inf ∅ = xn.

Nous allons distribuer aléatoirement tout x vers son prédécesseur et vers son successeur par la fonction ψ : ℝ × [0, 1] →{x1,...,xn} définie par

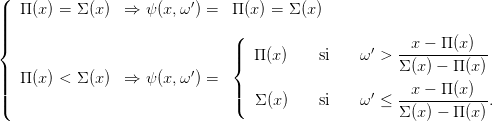( || Π (x) = Σ (x ) ⇒ ψ (x,ω′) = Π (x) = Σ (x ) ||| |{ (| ′ x − Π(x) |{ Π (x) si ω > Σ-(x-) −-Π-(x) ||| Π (x) < Σ (x ) ⇒ ψ (x,ω′) = ||| ||( ′ --x −-Π(x)--- ( Σ (x) si ω ≤ Σ (x ) − Π (x).
(31)

On discrétise alors la dynamique stochastique F par

F^ : {x1,...,xn} × 𝕌 × (Ω × [0,1],μ ⊗ dω′) → {x1, ...,xn }
(32)

où

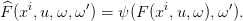^F (xi,u,ω,ω ′) = ψ (F(xi,u,ω ),ω′).
(33)

7.3 Discrétisation d’un problème d’optimisation stochastique sur ℝn

7.4 Discrétisation d’un problème d’optimisation déterministe sur ℝ et mise sous forme stochastique

Nous reprenons ce qui est fait ci-dessus, mais avec F déterministe.

La dynamique commandée dynamique_commandee est transformée en une famille de matrices de transition discretisation(etat,commande,dynamique_commandee) : partant d’un état xi et appliquant la commande ul, on transite vers les deux voisins encadrant dynamique_commandee(xi,ul) (ou un seul si on est en deçà ou au delà de {x1,...,xn}) avec une probabilité égale à la distance normalisée à ces points (ou égale à 1).

La macro Scilab suivantepredec_succes utilise la fonction dsearch, pas forcément disponible sur les versions les plus anciennes de Scilab. En cas de problème, la remplacer par le code à télécharger ici.

  function indices_image_discretisee=predec_succes(etat,image)
    //etat = vecteur ordonné
    //image = vecteur
    // indices_image_discretisee = liste
    //indices_image_discretisee(1)(i)=j
    // SSI etat(j) est le prédécesseur de image(i)
    //indices_image_discretisee(2)(i)= j
    // SSI etat(j) est le successeur de image(i)
    //indices_image_discretisee(3)(i)=
    //probabilité d'aller vers le prédécesseur de image(i)
  
    cardinal_etat=prod(size(etat));
    ind=dsearch(image,etat);
    // image(i) \in [etat(ind(i)), etat(ind(i)+1)[ sauf si
    // ind(i)=0, auquel cas image(i)<etat(1) ou image(i)>etat($)
    //ind_nd=ind(image_ind);
    image_ind_h=find(image > etat($));
    ind(image_ind_h)=cardinal_etat;
    // ind(i)=0 ssi image(i)<etat(1)
    // ind(i)=n ssi image(i)>etat($)
    image_ind_m=find(ind > 0 & ind < cardinal_etat);
    // indices du milieu : image(image_ind_m) \subset [etat(1),etat($)]
    // ind(image_ind_m) \subset ]0,n[
    image_ind_b=find(ind==0);
    // indices du bas : image(image_ind_b) <etat(1)
    image_ind_h=find(ind==cardinal_etat);
    // indices du haut : image(image_ind_h) >etat($)
  
    ind1=zeros(image);ind2=ind1;
    proba=zeros(image);
  
    ind1(image_ind_h)=ind(image_ind_h);
    // envoie les indices pour lesquels l'image de l'etat correspond est
    // >etat($) vers cardinal_etat, dernier indice de etat
    ind2(image_ind_h)=ind1(image_ind_h);
    // prédécesseur = successeur = etat($)
    proba(image_ind_h)=ones(image_ind_h);
    // probabilité 1 d'aller vers prédécesseur = successeur
  
    ind1(image_ind_m)=ind(image_ind_m);
    ind2(image_ind_m)=1+ind(image_ind_m);
    proba(image_ind_m)=(etat(1+ind(image_ind_m))-image(image_ind_m)) ./ ...
                       (etat(1+ind(image_ind_m))-etat(ind(image_ind_m)));
  
    ind1(image_ind_b)=ind(image_ind_b)+1;
    // +1 à cause de ind(image_ind_b) composé de 0
    // envoie les indices pour lesquels l'image de l'etat correspond est
    // <etat(1) vers 1, premier indice de etat
    ind2(image_ind_b)=ind1(image_ind_b);
    // prédécesseur = successeur = etat(1)
    proba(image_ind_b)=ones(image_ind_b);
    // probabilité 1 d'aller vers prédécesseur = successeur
  
    indices_image_discretisee=list();
    indices_image_discretisee(1)=ind1;
    indices_image_discretisee(2)=ind2;
    indices_image_discretisee(3)=proba;
  endfunction
  
  
  function z=egal(x,y)
    z=bool2s(x==y)
  endfunction
  
  
  function matrice_transition=discretisation(etat,commande,dynamique_commandee)
    matrice_transition=list()
    //etat = vecteur ordonné
    //commande = vecteur
    //dynamique_commandee = fonction(x,u)
    //matrice_transition = liste de matrices de transition 
    //  sur les indices de etat
    cardinal_etat=prod(size(etat));
    for l=1:prod(size(commande)) do
      //la liste matrice_transition est indicée par les indices du vecteur commande
      image=dynamique_commandee(etat,commande(l));
      // vecteur des images du vecteur etat
      indices_image_discretisee=predec_succes(etat,image)
      indices1=indices_image_discretisee(1);
      indices2=indices_image_discretisee(2);
      probabilites=indices_image_discretisee(3);
  
      M1=zeros(cardinal_etat,cardinal_etat);
      M2=zeros(M1);
      for i=1:cardinal_etat do
        M1(i,indices1(i))=probabilites(i);
        M2(i,indices2(i))=1-probabilites(i);
      end
      matrice_transition(l)=M1+M2
  
      //coincidmoins=feval(zmoins(1,:),etat,egal)
      // coincidmoins(i,j)=1 ssi zmoins(1,i) == etat(j)
      // ssi partant de etat(i), etat(j) est visité
      //coincidplus=feval(zplus(1,:),etat,egal)
      //coincidmoins=1-sign ( abs ( log( ( exp(-zmoins(1,:)') ) * exp(etat) )));
      //coincidplus=1-sign ( abs ( log( ( exp(-zplus(1,:)') ) * exp(etat) ) ) );
      //matrice_transition(l)= coincidmoins .* ( ones(etat)' * zmoins(2,:) )' +...
      //coincidplus .* ( ones(etat)' * zplus(2,:) )' 
      // affectation des probabilités
    end
  endfunction

7.5 Discrétisation d’un problème d’optimisation stochastique sur ℝN, N ≥ 2

On peut généraliser ce qui a été fait pour N = 1, en discrétisant ℝN sur une grille finie

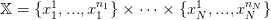𝕏 = {x1,...,xn1} × ⋅⋅⋅ × {x1 ,...,xnN } 1 1 N N
(34)

et en définissant des voisins 𝒱(x) ⊂ 𝕏 pour tout point x ∈ ℝN, avec des probabilités de transiter vers ces voisins.

On est alors ramené à une chaîne de Markov sur un espace fini 𝕏, qui a la particularité d’être un espace produit. Il reste alors à numéroter les éléments de 𝕏 pour se ramener à un problème d’optimisation stochastique sur des entiers.

Bien sûr, en terme de programmation informatique, ceci n’est pas si simple...