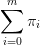
On se donne un graphe qui représente les liens entre des pages web sur un ensemble de pages données. Les noeuds du graphe sont les pages web et la présence d’un arc du noeud i au noeud j indique que la page j est référencée par la page i. Soit n le nombre total de pages, le graphe est donné par sa matrice d’adjacence Adj de taille nxn où Adj(i,j)==1 s’il existe un lien de la page i vers la page j et Adj(i,j)==0 sinon.
Le degré d’un noeud deg(i) est le nombre d’acs partant de ce noeud.
En divisant chaque ligne de la matrice Adj par son degré on obtient une matrice sous stochastique, Pss ou la somme en ligne vaut 0 pour les noeuds de degré nul et vaut 1 pour les autres noeuds.
On se donne aussi un vecteur ligne, z de taille n, dont les composantes sont strictement positives et dont la somme des composantes vaut 1.
On appelle P1 la matrice stochastique obtenue à partir de Pss en remplaçant les lignes nulles par le vecteur ligne z. On appelle P la matrice stochatique αP1 + (1 −α)ez où α est un réel donné 0 < α < 1 et e est le vecteur colonne de taille n dont toutes les composantes valent 1.
On considère une chaîne de Markov de matrice de transition P.
Question 1 Décrire le comportement de la chaîne (Xn)n∈ℕ. Pourquoi le vecteur z est appellé vecteur de téléportation.
Le PageRank des états de la chaîne de markov (qui sont les noeuds de notre graphe de pages web) est donné par la mesure invariante π associée à la chaîne.
Question 2 Que peut-on dire de π ? existence ? unicité ?
Construction et visualisation de matrices d’adjacences Adj aléatoires. Compléter le squelette de programme qui suit:
Question 3 La matrice P est stochastique mais présente le défaut d’être une matrice pleine alors que la matrice d’origine Pss était creuse. Montrer que le calcul de P′∗ x peut se faire en utilisant Pss′, d et z en préservant le caractère creux des opérations.
Question 4 Calculer le PageRank des pages du graphes en utilisant la fonction spec de scicoslab. On redessine le graphe en tenant compte du PageRank pour choisir le diamètre du cercle représentant chaque noeud.
Question 5 Calculer π en utilisant la suite pk+1 = P′∗ pk.
Question 6 Calculer π en utilisant la suite précédente mais en conservant Pss′, d et z.
On considère maintetant les m premiers états de la chaîne avec m = n∕2 et on cherche à maximiser le PageRank des m-premières pages.
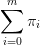 | (1) |
On suppose qu’on a accès aux p-premières pages (p ≤ m) et qu’on peut changer leurs liens vers les pages m + 1,…,n. On peut donc choisir de changer la sous matrice Adj(1:p,m+1:$) de la matrice Adj
Question 7 Écrire un programme d’optimisation discret qui résoud le problème de l’optimisation du pagerank (on choisira p = 2 et m = n∕2).
On cherche maintenant d’autres méthodes pour réaliser cette otpimisation de façon plus efficace.
On se donne un chaîne de Markov de matrice de transition P et une fonction coût r(x) on cherche à vérifier le théorème ergodique pour une matrice P irréductible.
![[T∑−1 ] ∑
lim -1𝔼 r(X ) = π(x)r(x)
T→+ ∞ T t
t=0 x](pagerank1x.png) | (2) |
On veut vérifier maintenant que c = ∑ xπ(x)r(x) s’obtient aussi en résolvant le système linéaire:
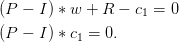
On va vérifier en effet que c1 est un vecteur constant dont les composantes valent c.
On verifie que (P − I) ∗ c = 0 impose à c d’être un vecteur constant.
Question 9 Suivre les calculs suivants dans scicoslab et conclure.
On peut donc résoudre le problème ergodique précédent en cherchant un couple (w,c) solution de
la composante c scalaire donnera la solution du problème ergodique.
On regarde un cas particulier ou la fonction coût pour un état i est donnée par
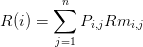 | (4) |
où P est la matrice de transition de la chaine et Rm est une matrice nxn donnée. On suppose aussi que la matrice de transtion à la forme particulière d’une matrice Google.
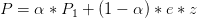 | (5) |
Question 10 Montrer que si w est un points fixe de l’opérateur w → αP1w + b où bi = ∑ jPi,jRmi,j alors (w,c) avec c = (1 − α) ∗ z ∗ w est solution de w + c = Pw + R.
Question 11 Que peut-on dire de l’opérateur w → αP1w + b ? en déduire une méthode numérique pour calculer son point fixe.
Soit Pν la matrice de transition obtenue pour un choix ν de redirections de liens au sein de la matrice d’adjacence de graphe. Si on regarde un problème ergodique avec une fonction coût r(x) = ∑ jPi,jνRm i,j on sait que le coût ergidique devient
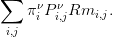 | (6) |
Pour un sous ensemble I de noeuds fixés et le choix Rmi,j = ξI(i) (où ξI(i) vaut 1 si i ∈ I et 0 sinon) le coût devient ∑ i∈Iπiν.
Le choix Rmi,j = ξI(i) permet d’obtenir un coût ergodique qui est le pagerank de I et on a vu dans la section précédente que le calcul du coût ergodique s’obtient aussi à partir de la solution de
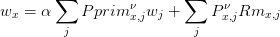 | (7) |
Si on cherche à maximiser le PageRank on va chercher à résoudre
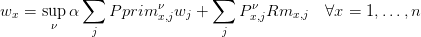 | (8) |
On suppose qu’on a accès aux m-premières pages et qu’on peut changer leurs liens vers les pages m + 1,…,n. On peut donc choisir de changer la sous matrice Adj(1:p,m+1:$) de la matrice Adj.
On va implémenter un algorithme d’iterations sur les valeurs pour touver une solution à l’équation (9).
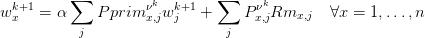 | (9) |
Question 12 Implémenter l’algorithme précédent.