Subway stations optimal energy management

Contents

1 Problem statement and data

Subway stations represent one third of the Paris subway system energy consumption. There are unexploited energy ressources in subway stations that could be harvested to lower this energy consumption. We could for example recover braking energy from the trains. Currently trains can dissipate their kinetic energy by braking mechanically or convert this energy into electricity. However supply/demand equilibrium have to be ensured on the subway line. Hence a train can brake electrically only if there is a train accelerating/consuming energy nearby. There is therefore a significant amount of potential energy that is currently wasted. We could overcome this problem with an electrical storage.

We consider a subway station equiped with a battery that can charge braking energy and national grid energy on one side (subway line side) and discharge energy to power the subway station which is also powered by the national grid (subway station side). A battery manager has to control this battery in real time. The station demand and the cost of electricity are assumed deterministic. Braking energy available at each time step is uncertain.

We present hereby the stochastic optimization problem we want to solve:

We detail all notations and equations in the following.

1.1 Battery dynamics

The battery can store power coming from the trains or the national grid and supply power to the subway station. It cannot do both things at the same time. We control its state of charge (soc). We model the dynamics of the battery at each time step t by a function f_t we call the dynamic at time t giving equation (1b) :

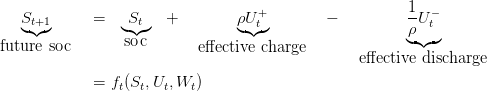
where

• t ∈ 𝕋 := {0, 1,…,T − 1} is discrete (minutes in this case) and t denotes the beginning of the period [t,t + 1[. We call T the horizon of the problem.
• S_t state of charge (kWh) of the battery at the beginning of period [t,t + 1[. It belongs to a set 𝕏 = [S_min,S_max] representing the minimum and maximum state of charge of the battery.
• U_t energy (kWh) of battery charge or discharge during [t,t+1[, decided at the beginning of time period [t,t + 1[. It belongs to a space 𝕌 = [U_min,U_max] modeling ramp limits for the charge or discharge.
• U_t⁻ = − min (0,U _t) energy we discharge from the battery
• U_t⁺ = max (0,U(t)) energy we charge into the battery
• ρ is the charge and discharge efficiency (%)

The initial state of charge of the battery is called x₀ and appears in the equality constraint (1g)

1.1.1 Variables definition

We define hereby the remaining variables of the problem presented in figure1

• E_t^s energy (kWh) we pay to the national grid to power the station during [t,t + 1[
• E_t^l energy (kWh) we pay to the national grid to charge the battery during [t,t + 1[
• D_t energy (kWh) consumed by the subway station during [t,t + 1[
• W_t braking energy (kWh) available on the subway line during [t,t + 1[. This quantity is a random variable

We observe that charge/discharge decision U_t is taken at the beginning of [t,t + 1[, before knowing the available braking energy W_t. We are in a decision-hazard setting.

1.1.2 Constraints

We have to ensure the supply/demand equilibrium at each node and each time step on the subway station node which leads to equation:

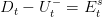(2)

On the subway line node we have to ensure supply/demand balance however we are not forced to recover all the regenerative braking energy W_t. We have then an inequality constraint (1d):

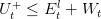We prevent the battery manager to sell power to the grid then we have to ensure:

1.2 Criterion: intertemporal payoff

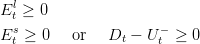
At each time t we pay to the national grid operator the quantity E_t^l + E _t^s of energy. We assume that the price of electricity c_t per kWh is known in advance as it is negociated and constant during [t,t + 1[.

At each time t we pay the instantaneous cost:

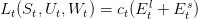Using equation (2) we can eliminate the variable E_t^s leading to the instantaneous cost:

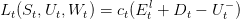At the end of the horizon we have no preference concerning the final state of charge of the battery. We introduce then a final cost function K : 𝕏 → ℝ such as:

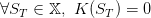From 0 to T the payoffs sum up to:

(3)

The manager wants to minize these payoffs every day without knowing the future availability of braking energy. He will therefore minimize them on average, hopefully obtaining the best mean payoff he can obtain after several days. The manager wants to minimize the expected payoff:

(4)

The manager wants to solve problem (1). We detail the last constraint (1i) in the following.

1.3 Numerical data and model

1.3.1 Constants

We define, in file constants.jl, some numerical data required to model the problem.

1.3.2 Braking energy scenarios

We provide a code function, defined in scenarios_generation.jl , that allows to compute a given number of braking energy scenarios over the time horizon.

1.3.3 Problem functions declaration

We define here 4 code functions required to model the problem.

2 Evaluation with given policies

The manager wants to be able to make a decision that takes into account the future uncertainties but that use the information about the past uncertainties realization. This is the meaning of the last constraint (1i) of problem (1) we did not yet explained.

2.1 Non-anticipativity constraint

The constraint U_t = π_t(W₀,...,W_t−1) states that the decision at time t, U_t, must depend only on the past uncertainties of the problem W₀,...,W_t−1.

When the W_t are time independent we can restrict the search to functions of the current state of the problem. The non anticipativity constraint becomes U_t = π_t(S_t). When the W_t are not time independent we can still restrict the search to functions of the state. The controls obtained are not guaranteed to be optimal but they may be good enough and are often easier to compute.

An admissible state feedback policy π : 𝕋 × 𝕏 → 𝕌 assigns a charge or discharge instruction  U_t = π_t(S_t) ∈ 𝕌 to any time t ∈ 𝕋 and to any state of charge S_t ∈ 𝕏, while respecting the problem constraints. Given an admissible policy π and given a braking energy scenario W(⋅) = W₀,…,W_T−1, we are able to build a battery state of charge trajectory S(⋅) := S₀,…,S_T−1,S_T and a charge/discharge control trajectory U(⋅) := U₀,…,U_T−1 produced by the “closed-loop” dynamics initialized at the initial time 0 by

We also obtain the payoff associated to the braking energy generation scenario W₁,...,W_T :

(6)

where S(⋅) and U(⋅) are given by (5).

The expected payoff associated with the policy π is

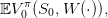(7)

where the expectation 𝔼 is taken with respect to the product probability ℙ. The true expected value (7) is difficult to compute,¹ and we evaluate it by the Monte Carlo method using N_s braking energy scenarios W¹(⋅),…,W^N_s(⋅):

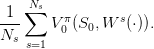(8)

By the law of large numbers, the mean payoff (8) is a “good” approximation of the expected payoff(7) if the number of scenarios is “large enough”.

2.2 Simulation of a given heuristic

We propose here a code function providing a heuristic strategy base only on state and time information. At time t this function return a control u_t knowing t and x_t. This code function is then a state feedback. Its idea is to charge during peak hours and discharge during off-peak hours while ensuring the state and control constraints.
  

We provide a code function, in policy_assessment.jl, to assess a policy along multiple scenarios knowing the instantaneous cost, the final cost, the dynamic, the scenarios, the initial state of the system and the policy.

3 Stochastic Dynamic Programming resolution

Stochastic Dynamic Programming is a method to solve Stochastic Optimal Control problems. It is based on the concept of value functions and the so called Bellman’s principle of optimality. The value function of the problem at time t is defined as:

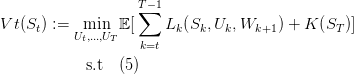
With K the final cost of the problem which is zero in our case. The principle of optimality states that, when the problem noises are independent, we can write the following recursion between value functions:

(9)

In practice we use equation (9) in two phases: an offline stage where we use it to compute value functions, and an online stage where these functions are used to compute a control.

Offline phase: computation of value functions   
For t from T to 0 compute

(10)

Online: computation of a control   
At time t, knowing the state of the system S_t compute U_t:

(11)

In practice we compute the value functions on a discretized state space 𝕏^d. As it is not possible to iterate over a continuous set. Similarly we solve problems (19) and (20) by discretizing 𝕌 and testing every control in 𝕌^d the discrete space obtained.

3.1 Markovian assumption, state and control discretization

In order to compute the expectation in problems (19) and (20) we assume that the noises are time independent and use 1000 braking energy scenarios to compute the marginal laws of the noises at each time step. We do not use the assessment scenarios in order not to bias the results. The discrete marginal laws are obtained by quantization as Monte Carlo should be avoided as much as possible with Dynamic Programming.

We choose the size of the discretization step for the state variable and the control variable.

3.2 Value functions offline computation

We provide a function to compute the value functions of the problem.

3.3 Using value functions for online control computation

We provide a function, in file sdp_policies.jl to generate a control at time t knowing the previous uncertainty realization, the state of the system and the time step.

This function is a policy that can be plugged in our simulator.

4 Model Predictive Control

Model Predictive Control is a popular method to solve Stochastic Optimal Control problems arising in many engineering fields (electrical, mechanical...). Its popularity comes from its simplicity and accessibility. It consists in making a forecast to get rid of all the future uncertainties at each time step. We can then solve a deterministic problem which provides a control trajectory. We apply the first control. At the next time step we compute a new forecast and we reoptimize.

This algorithm has no offline phase.

Online: computation of a control   
At time t, knowing the state of the system S_t and the past uncertainties W₀,..,W_t−1 compute a forecast w_t,..,w_T−1 and compute U_t:

(12)

4.1 Deterministic problem resolution

We provide a function to solve a deterministic problem knowing a scenario, the initial state and the initial time step. This function is in the file deterministic.jl.

4.2 Model Predictive Control simulation

We provide a function to compute a forecast at time t for the next time steps up to the rolling horizon length knowing only the state at time t.

This function is used in the MPC policy as it consists in making a forecast of the future time steps and solve a deterministic problem.

5 Taking into account non-Markovian structure

We could improve the Model Predictive Control results. Indeed MPC performances depend significantly on the forecast quality. Here we use only information about the state of the system at time t to compute a forecast assuming all the noises are time independent. We the use the previous marginal laws to compute the forecast.

The scenario generator we provided follows the following rules:

• there is no braking energy during the night as subways are not circulating then ∀t ∈{T_stop,...,T_start}, W_t = 0
• during operating hours we model regenerative braking randomness by an autoregressive process of order 1:

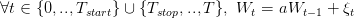  (13)

  with (ξ_t)_t∈𝕋 a sequence of gaussian white noises.

5.1 Improving MPC forecast

The forecast computed at each time step in the MPC strategy could be based on this model and on the last uncertainty realization. The MPC policy is not anymore a state feedback it lies in the class of mappings:

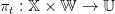(14)

We provide a MPC policy using this information

We can build such kinds of policies in a dynamic programming framework as well.

5.2 Using past informations online in classical SDP

We consider the value functions computed at section ??. During the online phase we can compute the expectation with respect to W_t by exploiting the stochastic process structure. We know here that W follows an autoregressive process (or zero during night hours). We know then that: 𝔼[g(W_t)|W_t−1 = w_t−1] = 𝔼[g(aw_t−1 + ξ_t)]. Knowing the law of ξ_t we can therefore estimate the conditional expectation at time t.

Offline phase: computation of value functions   
Ignore the dependence between the noises. We keep the same marginal laws for the random variables. For t from T to 0 compute

(15)

Online: computation of a control   
At each time step t, observing state S_t and previous uncertainty realization w_t compute U_t:

(16)

We provide a policy of this form using the value functions we generated earlier.

5.3 State augmentation

Using noises correlation information with value functions computed with time independence assumption mitgh be inefficient in practice.

When the randomness is an order 1 autoregressive process it is possible to improve the stochastic dynamic programming results by augmenting the state with 1 state variable. W follows an AR(1) process. We can then take W_t as a state variable, ξ(⋅) being the noises of the problem. We just add the following dynamic in the problem (1):

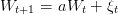(17)

W(⋅) being now a state variable and ξ(⋅) the exogenous noises process. We call the new dynamic F_t such that:

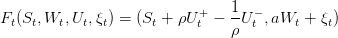(18)

Offline phase: computation of value functions   
For t from T to 0 compute

(19)

Online: computation of a control   
At time t, knowing the state of the system S_t compute U_t:

(20)

We define a new instantaneous cost code function, a new dynamic, a new state discretization, a new control discretization and new noises laws.

5.4 Value functions generation and forward simulation

We build another stochastic dynamic programming model. We can generate the value functions of the problem with 2 state variables. Now the noises are truly independent.

We provide a function to compute a control online using these value functions. This is a state feedback with the augmented state. It is therefore a function of S_t and W_t.

5.5 Benchmark