Modali 2005

Jean-Philippe Chancelier and Michel de Lara
(last modification date: October 10, 2017)
Version pdf de ce document
Version sans bandeaux

1 Random walk on ℤ
2 Random walk on ℤ2
3 Transmitting 0 and 1
4 Testing the irreductibility of a Markov chain
5 Une option européenne discrète
6 Le problème de la secrétaire

Contents

1 Random walk on ℤ
2 Random walk on ℤ2
3 Transmitting 0 and 1
4 Testing the irreductibility of a Markov chain
5 Une option européenne discrète
6 Le problème de la secrétaire

1 Random walk on ℤ

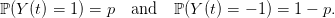
Let (Y (t))t∈ℕ be a sequence of i.i.d. random variables having values in {−1, +1} as follows:

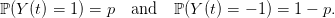ℙ(Y (t) = 1) = p and ℙ (Y (t) = − 1) = 1 − p.
(1)

We define a stochastic process (X(t))t∈ℕ on ℤ called random walk by

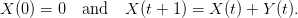X (0) = 0 and X (t + 1) = X (t) + Y (t).
(2)

Question 1 Simulate one single trajectory for p = 0.5.

T= 100;  
time=1:(T+1);  
p=0.5;  
trajectory=zeros(time) ;  
// vector will contain the trajectory X(0),...,X(T)  
for t=1:T  
trajectory(t+1)=trajectory(t) + ( 2*grand(1,1,'bin',1,p)-1 ) ;  
end ;  
xset("window",1); xbasc(1); plot2d2(time,trajectory);  
xtitle('Random walk (p='+string(p)+')', 'time (t)','X(t)')

Question 2 Draw four trajectories for p = 0.5 on the same picture.

S=4;  
trajectory=zeros(S,sum(prod(ones(time))));  
// vector will contain the S trajectories X(0),...,X(T)  
for s=1:S,  
for t=1:T  
trajectory(s,t+1)=trajectory(s,t) + ( 2*grand(1,1,'bin',1,p)-1 ) ;  
end ;  
end  
xset("window",2); xbasc(2); plot2d2(time',trajectory(1:S,:)' );  
xtitle('Random walk (p='+string(p)+')', 'time (t)','X(t)')  

PICT

Figure 1: Four trajectories of the symmetric random walk on ℤ

Question 3 Take p ⁄= 0.5 and redo simulations.

2 Random walk on ℤ2

Let (Y (t))t∈ℕ be a sequence of i.i.d. random variables having values in {−1, +1}2 as follows:

∑ ℙ(Y (t) = (𝜖,𝜖′)) = p 𝜖,𝜖′ with p𝜖,𝜖′ = 1. (𝜖,𝜖′)∈{−1,+1}2
(3)

We define a stochastic process (X(t))t∈ℕ on ℤ2 called 2-dimensional random walk by

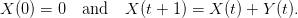X (0) = 0 and X (t + 1) = X (t) + Y (t).
(4)

Question 4 Simulate trajectories for p𝜖,𝜖′ = 0.25.

T= 100;  
time=1:(T+1);  
p=0.5;  
trajectory=zeros(2,T+1) ;  
// vector will contain the trajectory X(0),...,X(T)  
for t=1:T  
trajectory(:,t+1)=trajectory(:,t) + ( 2*grand(2,1,'bin',1,p)-1 ) ;  
end ;  
xset("window",1);xbasc(1); plot2d(trajectory(1,:),trajectory(2,:),...  
style=3,...  
rect=[-maxi(abs(trajectory(1,:))),-maxi(abs(trajectory(2,:))),...  
maxi(abs(trajectory(1,:))),maxi(abs(trajectory(2,:)))] );  
xtitle('Symmetric random walk', 'time (t)','X(t)')

3 Transmitting 0 and 1

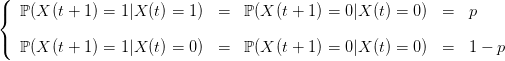( { ℙ (X (t + 1) = 1|X (t) = 1) = ℙ(X (t + 1) = 0|X (t) = 0) = p ( ℙ (X (t + 1) = 1|X (t) = 0) = ℙ(X (t + 1) = 0|X (t) = 0) = 1 − p
(5)

may be simulated by

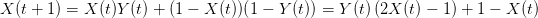X (t + 1) = X (t)Y (t) + (1 − X (t))(1 − Y (t)) = Y (t)(2X (t) − 1) + 1 − X (t)
(6)

where (Y (t))t∈ℕ is a sequence of i.i.d. random variables with Bernoulli law ℬ(p; 1).

T= 100;  
time=1:(T+1);  
p=0.9;  
trajectory=zeros(time) ;  
// vector will contain the trajectory X(0),...,X(T)  
for t=1:T  
trajectory(t+1)= (2*trajectory(t)-1)*grand(1,1,'bin',1,p) + ...  
1- trajectory(t)  
end ;  
xset("window",1); xbasc(1); plot2d2(time,trajectory, rect=[0,-0.1,T,1.1]);  
xtitle('0 or 1 (p='+string(p)+')', 'time (t)','X(t)')

4 Testing the irreductibility of a Markov chain

On utilise Scilab pour visualiser le graphe associé à une chaîne de Markov :

 M  = [    0.1    0.7    0.     0.1    0.     0.1  
           0.     0.3    0.7    0.     0.     0.  
           0.     0.4    0.6    0.     0.     0.  
           0.     0.     0.     0.7    0.     0.3  
           0.     0.8    0.     0.     0.1    0.1  
           0.     0.     0.     0.8    0.     0.2 ];  
 Mb=M<>0 ; //  Matrice Booléene associée  
 g=mat_2_graph(sparse(bool2s(Mb)),1,'node-node'); //  Graphe  associé  
 n = size(M,'r');  
 theta = (2*%pi/n)*(1:n);  
 g('node_x')=sin(theta)*100;  
 g('node_y')=cos(theta)*100;  
 show_graph(g);

On peut trouver les classes de la chaîne de Markov en cherchant les composantes (fortement) connexes du graphe associé.

[nc,ncomp]=strong_connex(g); // Calcul des composantes connexes

Question 5

  1. Dans les composantes connexes recherchez celles qui correspondent à des classes finales.
  2. Construire la permutation des états qui permet d’écrire M sous la forme canonique où on voit tout de suite les classes finales et la classe transitoire :
    Mc=M(perm,perm)  // Forme canonique de M.  
     Mc  =  
     
    !   0.2    0.8    0.     0.     0.     0.  !  
    !   0.3    0.7    0.     0.     0.     0.  !  
    !   0.     0.     0.3    0.7    0.     0.  !  
    !   0.     0.     0.4    0.6    0.     0.  !  
    !   0.1    0.     0.8    0.     0.1    0.  !  
    !   0.1    0.1    0.7    0.     0.     0.1 !

5 Une option européenne discrète

La marche aléatoire de Cox Ross est définie de la façon suivante : soient a et b deux nombres réels et soit (Un)n≥0 une suite de variables aléatoires indépendantes de loi commune :

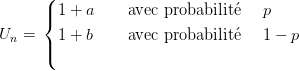( |{ 1 + a avec probabilit´e p Un = 1 + b avec probabilit´e 1 − p |(

avec 0 < p < 1. On défini alors une suite de variables aléatoires (Sn)n∈ℕ par :

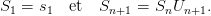S1 = s1 et Sn+1 = SnUn+1.

On a vu en cours que la suite Sn est une chaîne de Markov : Supposons que l’on s’intéresse au temps n ∈ [0,N], comme Sn = s1 ∏ i=1nU i, l’espace d’état de la chaîne (Sn)n∈ℕ est alors fini, ℰ = {γi,j ≡ s1(1 + a)i(1 + b)j, 0 ≤ i + j < N}. On vérifie que S n est une chaîne de Markov homogène de matrice de transition:

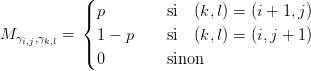( |{ p si (k, l) = (i + 1,j) M γ ,γ = 1 − p si (k, l) = (i,j + 1) i,j k,l |( 0 sinon
(7)

La suite Sn précédemment définie peut servir à modéliser le cours d’un actif. On cherche à calculer pour s1 fixé la valeur :

[ ] ----1---- v1(s1) = 𝔼 (1 + r)N f(SN )|S1 = s1 .
(8)

On a vu en cours que cette quantité peut se calculer de façon récursive en calculant pour n allant de N à 0 les quantités :

[ ] vn(x) = 𝔼 -----1-----f(SN )|Sn = x . (1 + r)N− n
(9)

On se propose dans cet exercice de calculer vn(x) récursivement pour obtenir v1(s1). On utilisera les données suivantes :

a= 0.05;  
b= -0.05;  
s0=1 ;  
r=0.01;  
pa = (r-a)/(b-a);  
pb = (b-r)/(b-a);

Les états possibles de la chaîne sont indicés par un couple (i,j) avec i ∈ [0,N] et j ∈ [0,N] et on veut dans Scilab utiliser une matrice V pour stocker la fonction v(x,n). Il faut donc pouvoir coder les états avec un unique indice et on retiendra i + N ∗ j + 1. La matrice utilisée dans Scilab sera de taille V (N2,N) (on ne cherche pas dans un premier temps à économiser de la place mais on privilégie du calcul matriciel).

Question 6

  1. Construire une matrice s(N,N) qui contient les états possibles de la chaîne. Utiliser la fonction matrix pour transformer s en un vecteur colonne de taille NxN.
  2. Initialiser une matrice V de taille (NxN,N).
  3. On suppose que f(x) = (x − 1)+. Initialiser la dernière colonne de V (V(:,N)) avec la fonction f et en utilisant le vecteur colonne contenant les états possibles.
  4. calculer récursivement V(:,n) en utilisant les résultats du cours. On notera que pour certains états à l’instant n les états possibles à l’instant n + 1 sont hors de l’ensemble [1,N] mais ce n’est pas grave car la valeurs de V(:,n+1) en ces points n’interviennent pas dans le calcul de v1(s1). On pourra donc utiliser zéro comme valeurs de V en ces points.
  5. Pour les points atteignables à partir de s1 tracer les courbes V (:,n).

6 Le problème de la secrétaire

On rappelle ici la formulation vue en cours. On dispose de N objets de valeurs vk ( v1 < v2 < … < vN ) inconnues que l’on tire au hasard (de façon équiprobable) les uns après les autres. Quand on tire le k-ième objet on peut soit le choisir et s’arrêter soit continuer. Les objets que l’on va tirer successivement auront pour valeur vσ(k) où σ est une permutation de [1,N] et toutes les suites (vσ(k))k=1,N sont équiprobables.

Introduisons les notations suivantes :

{ 1 si W = k avec W = arg max v Sk = k k j∈ [1,k] σ(j) 0 sinon

On a vu que la suite Sn est une chaîne de Markov. L’espace d’état de Sk est {0, 1} et les Matrices de transition M(k) vérifient : M i,1(k) = 1∕(k + 1) et M i,0(k) = k∕(k + 1) (les S k sont en fait indépendants).

Le problème du décideur est un problème d’arrêt optimal. Il cherche à calculer u1(1) et obtenir la stratégie optimale associée (noter que S1 ≡ 1), où un(x) est donné par la formule générale :

un (x) ≡ sup 𝔼 [g τ(S τ)|Sn = x]. τℱnt.a.,n≤τ≤N

avec gk(1) = k∕N et gk(0) ≡ 0.

On rappelle que un(x) est solution de l’équation suivante :

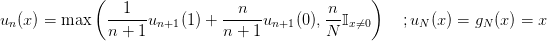( 1 n n ) un (x ) = max -----un+1 (1) + -----un+1 (0 ), --𝕀x⁄=0 ;uN (x) = gN (x) = x n + 1 n + 1 N
(10)

Question 7

  1. Écrire un programme qui calcule la fonction un(x) pour n ∈ [1,N] et tracer les courbes un(1) et un(0) ainsi que les fonctions gn(1) et gn(0).
  2. On suppose que les valeurs des secrétaires sont [1,N]. Utiliser grand pour en tirer une permutation aléatoire.
  3. Calculer le long de cette trajectoire la valeur de un et trouver le temps d’arrêt i.e l’indice de la secrétaire choisie.
  4. Illustrer graphiquement les résultats précédents.