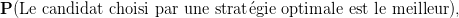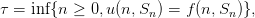Contents
Les programmes suivant on été prévu pour être exécutés à l’aide Scicoslab. Ce
programme peut être téléchargé librement sur www.scicoslab.org. Il est disponible sur
MacOSX, Windows ou Linux (Debian, Ubuntu ou Fedora). Noter toutefois qu’il faut installer le
server X, XQuartz sur MacOSX. Ces programmes peuvent aussi fonctionner, moyennant de
légère modification, avec la version officielle de Scilab.
Le fichier source en Scilab correspondant à ce document est arret_scilab_ddi.sci. Il est
partiellement mais pas totalement corrigé. Le correction complète arret_scilab_ddi_corrige.sci
sera accessible à la fin du TD.
1 Le calcul du prix d’une option “américaine”
Rappel : le cas européen (calcul d’espérance)
On considère le modèle de Cox-Ross :
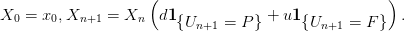
On choisit les valeurs numériques de la façon suivante
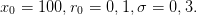
et l’on définit p, r, u et d en fonction de N de la façon suivante :
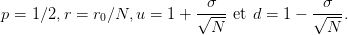
On cherche à évaluer E(f(N,XN)) où
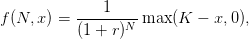
avec K = x0 = 100 et r = 0, 05.
-
1.
- Calculer ces prix d’options européennes (call et put) se ramène à des calculs d’espérance
d’une fonction d’une chaîne de Markov. On implémente ici la méthode de calcul
d’espérance par “programmation dynamique”.
function res=gain_put(x,K) res=max(K-x,0);endfunction
function res=gain_call(x,K) res=max(x-K,0);endfunction
function res=inc(n) res=n+1;endfunction; function res=prix_eu(x_0,N,gain)
U=zeros(inc(N),inc(N));
for k=[0:N] do U(inc(N),inc(k))=gain(x_0*u^k*d^(N-k),K)/(1+r)^N;
end; for n=[N-1:-1:0] do
U(inc(n),inc(0):inc(n))=p*U(inc(n+1),inc(1):inc(n+1))+ ...
(1-p)*U(inc(n+1),inc(0):inc(n)); end;
res=U(inc(0),inc(0)); endfunction; function res=prix_eu_n(n,x_0,N,gain)
res=prix_eu(x_0,N-n,gain); endfunction
-
2.
- On peut vérifier que lorsque p = 1∕2 (ou r = 0) et x = K le prix des puts et des calls
coïncident. Pour le choix classique (1 + r −d)∕(u−d) (et r ⁄= 0), les prix sont différents,
ce que l’on vérifie aussi.
function main_1() r_0=0.05;sigma=0.3; x_0=100;K=100;
N=50; d=1-sigma/sqrt(N);u=1+sigma/sqrt(N); r=r_0/N;
p=1/2;K=x_0; p_put=prix_eu_n(0,x_0,N,gain_put);
p_call=prix_eu_n(0,x_0,N,gain_call); if abs(p_put-p_call) >= 1000*%eps then
printf("WARNING: ces deux prix devrait coincider: %f <> %f\n",p_put,p_call);
else printf("Parfait!\n"); end p=(1+r-d)/(u-d);
printf("Prix du call : %f\n",prix_eu_n(0,x_0,N,gain_call));
printf("Prix du put : %f\n",prix_eu_n(0,x_0,N,gain_put)); endfunction
-
3.
- Voici un programme qui permet de calculer des histogrammes. Si varargin est vrai un
dessin est tracé, sinon seul l’histogramme est retourné dans H.
function H=histo_discret(samples,maxsize,plot_flag) if exists('%nsp') then
H=histo_discret_nsp(samples,maxsize,plot_flag); else
H=histo_discret_scilab(samples,maxsize,plot_flag); end
endfunction function H=histo_discret_scilab(samples,maxsize,plot_flag)
H=0
for k=0:maxsize do
H(k+1)=length(find(samples==k)) ./size(samples,'*'); end;
if plot_flag then xbasc;plot2d3(0:maxsize,H);
f=gcf(); Dessin=f.children(1).children(1).children(1);
Dessin.thickness=10;Dessin.foreground=5; end; endfunction
function H=histo_discret_nsp(samples,maxsize,plot_flag) if nargin <= 2 then plot_flag=%f;end
H=zeros(1,maxsize+1);
[y,ind,occ]=unique(samples); H(y+1)=occ ./size(samples,'*'); if plot_flag then
xbasc;plot2d3(0:maxsize,H,line_color = 2,line_thickness = 10); end; endfunction
Le cas américain (arrêt optimal)
On s’intéresse au cas d’un option américaine qui promet (en valeur actualisée en 0), si on
l’exerce à l’intant n pour une valeur de Xn valant x
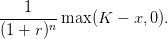
On cherche à calculer son prix donné par
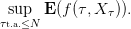
-
4.
- On pose v(n,x) = (1 + r)nu(n,x), vérifier en utilisant l’équation qui définit u dans le
cours, que v est solution de
![( [ ]
|{ v(n,x) = max pv(n-+-1,xu-)+-(1−-p)v(n-+-1,xd),(K − x )+ ,n < N, x ∈ E
1+ r
|(
v(N, x) = (K − x)+,x ∈ E.](arret_scilab_ddi6x.png) | (1) |
-
5.
- Ecrire un algorithme récursif (et inefficace ...) pour le calcul de v en recopiant
l’équation (1)
function res=prix_recursif_am(x,k,N,gain) if k==N then res=gain(x);return;end;
res=max(res/(1+r),gain(x)); endfunction
function res=prix_slow_am(x,N,gain) res=prix_recursif_am(x,0,N,gain); endfunction
-
6.
- Ecrire un algorithme efficace de calcul de v(n,x) (le prix de l’option américaine en n).
function res=prix_am(x_0,N,gain)
U=zeros(N+1,N+1); x=x_0*u .^[0:N] .*d .^[N:-1:0];
U(N+1,1:N+1)=gain(x);
for n=[N-1:-1:0] do
U(n+1,1:n+1)=p*U(n+2,2:n+2)+(1-p)*U(n+2,1:n+1);
U(n+1,1:n+1)=U(n+1,1:n+1)/(1+r);
x=x_0*u .^[0:n] .*d .^[n:-1:0];
end; res=U(1,1); endfunction; function res=prix_am_n(n,x_0,N,gain)
res=prix_am(x_0,N-n,gain); endfunction
-
7.
- Pour N = 10, comparer les 2 méthodes pour vérifier que tout fonctionne. Effectuer des
calculs de prix avec des N plus grands (uniquement pour la deuxième méthode, bien sûr).
function main_2() sigma=0.3;r_0=0.1; K=100;x_0=100;
N=10; r=r_0/N; d=1-sigma/sqrt(N);u=1+sigma/sqrt(N);
p=(1+r-d)/(u-d); prix_am(x_0,N,gain_put)
prix_slow_am(x_0,N,gain_put)
p1=prix_slow_am(x_0,N,gain_put);
p2=prix_am(x_0,N,gain_put); if (abs(p1-p2) >= 100*%eps) then
printf("WARNING: ces deux prix devrait coincider: %f <> %f\n",p1,p2); else
printf("Parfait!\n"); end N=1000;d=1-sigma/sqrt(N);u=1+sigma/sqrt(N);
prix_am(x_0,N,gain_put) endfunction;
-
8.
- Tracer les courbes de prix américaines et européennes x → v(0,x) pour x ∈ [80, 120] et
les supperposer au “payoff”.
function main_3() N=50; sigma=0.3;
p=1/2;d=1-sigma/sqrt(N);u=1+sigma/sqrt(N); K=100;x_0=100; r_0=0.1;
r=r_0/N; vmin=50; vmax=150; n=0; for x=[vmin:vmax] do n=n+1;
end
plot2d([vmin:vmax],courbe_eu,style = 2); plot2d([vmin:vmax],courbe_am,style = 3);
plot2d([vmin:vmax],gain_put([vmin:vmax]),style = 4); endfunction;
-
9.
- Regardez comment le prix évolue au fils du temps : tracez les courbes x → v(n,x), pour
n = 10, 20, 30, 40, 50.
function main_4() sigma=0.3; K=100;x_0=100; N=50;
p=1/2;d=1-sigma/sqrt(N);u=1+sigma/sqrt(N); r_0=0.1;r=r_0/N;
vmin=50;vmax=150;
for n=[0,10,20,30,40,45,47,49,50] do i=0; for x=[vmin:vmax] do
i=i+1; end
plot2d([vmin:vmax],courbe_am); end endfunction
-
10.
- Que constatez vous lorsque N augmente (N = 10, 100, 200, 500) et que l’on choisit r, u et
d en fonction de N comme définis plus haut.
Commentaire:
lorsque N vers +∞ dans ces conditions, on converge vers le prix dans un modèle continu
(et célèbre : le modèle de Black et Scholes). Dans le cas européen, le résultat se prouve
grâce au théorème de la limite centrale. Dans le cas américain, c’est un peu plus
compliqué!
function main_5()
sigma=0.3; K=100;x_0=100;
r_0=0.1; p=1/2; N=50;
r=r_0/N; d=1-sigma/sqrt(N);
u=1+sigma/sqrt(N); vmin=50;vmax=150; for N=[5,10,20,30,50] do r=r_0/N;
d=1-sigma/sqrt(N); u=1+sigma/sqrt(N); n=0; for x=[vmin:vmax] do
n=n+1; courbe(n)=prix_am(x,N,gain_put); end plot2d([vmin:vmax],courbe);
plot2d([vmin:vmax],max(K-[vmin:vmax],0)); end endfunction
-
11.
- Ecrire une fonction qui simule le vecteur (Bin(1),…,Bin(N)) du nombre de pile cumulé
dans des N tirages à pile ou façe (p, 1 − p).
Par la suite le valeur X(n) du modèle de Cox-Ross à l’instant n s’écrira :
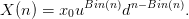
function res=simul_bin(N,p)
bin=grand(1,N,"bin",1,p);
endfunction;
-
12.
- Calculer la prix américain en conservant dans un vecteur V(t,k) les valeurs en
l’instant t − 1 et au point X(n) = x0uk−1dn−(k−1). Le décalage de 1 est du, comme
d’habitude, au fait que les tableaux sont indicés à partir de 1 en
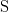 cicosLab.
cicosLab.
function V=prix_am_vect(x_0,N,gain)
V=zeros(N+1,N+1);
x=x_0*u .^[0:N] .*d .^[N:-1:0];
V(N+1,1:N+1)=gain(x); for n=[N-1:-1:0] do
V(n+1,1:n+1)=p*V(n+2,2:n+2)+(1-p)*V(n+2,1:n+1);
V(n+1,1:n+1)=V(n+1,1:n+1)/(1+r);
x=x_0*u .^[0:n] .*d .^[n:-1:0];
V(n+1,1:n+1)=max(V(n+1,1:n+1),gain(x)); end; endfunction;
-
13.
- A partir d’une trajectoire du modèle de Cox-Ross donnée par le vecteur Bin et des
valeurs de V précédemment calculées, évaluer le temps d’arrêt optimal associé à cette
trajectoire.
function res=temps_optimal_option(Bin,V,gain)
if gain(x_0)==V(1,1) then res=0;return;end; for n=1:size(Bin,'*')-1 do
x=x_0*u .^Bin(n)*d .^(n-Bin(n));
end; res=N; endfunction
-
14.
- Simuler un grand nombre de trajectoires du modèle de Cox-Ross et les valeurs des temps
d’arrêt associés à ces trajectoires. Tracer un histogramme de la loi du temps d’arrêt
optimal. Faire varier les valeurs de x0 (x0 = 60, 70, 80, 100, 120)) et voir l’influence de ce
choix sur le loi du temps d’arrêt optimal.
function tau=un_test(x_0,N) sigma=0.3; p=1/2;d=1-sigma/sqrt(N);u=1+sigma/sqrt(N);
K=100; r_0=0.1; r=r_0/N; V=prix_am_vect(x_0,N,gain_put);
Nbre=1000; for j=1:Nbre do Bin=simul_bin(N,p);
tau(j)=temps_optimal_option(Bin,V,gain_put); end histo_discret(tau,max(tau),%t);
endfunction; function main_6()
N=100; x_0=100;tau=un_test(x_0,N); endfunction; function main_7()
N=50; x_0=60;tau=un_test(x_0,N);
x_0=70;tau=un_test(x_0,N);
x_0=80;tau=un_test(x_0,N);
x_0=100;tau=un_test(x_0,N); x_0=120;tau=un_test(x_0,N);
endfunction;
-
15.
- Traiter le cas du call. On peut montrer qu’il ne s’exerce qu’à l’échéance. Le vérifier par
simulation.
function main_8()
function res=gain_call(x) res=max(x-K,0);
endfunction sigma=0.3;r_0=0.1; K=100;x_0=100; N=50;
r=r_0/N; u=(1+r)*exp(sigma/sqrt(N));d=(1+r)*exp(-sigma/sqrt(N));
p=1/2;
V_call=prix_am_vect(x_0,N,gain_call); Nbre=1000; for j=1:Nbre do
Bin=simul_bin(N,p); tau(j)=temps_optimal_option(Bin,V_call,gain_call);
end histo_discret(tau,max(tau),%t); endfunction;
-
16.
- Évaluer la probabilité d’exercice anticipé (i.e. P(τ < N), si τ est le temps d’arrêt optimal.
Vérifier par simulation que cette probabilité est strictement positive (pour le put) si
r > 0.
function proba=compute_proba(x_0,N) sigma=0.3;
p=1/2;d=1-sigma/sqrt(N);u=1+sigma/sqrt(N); K=100; r_0=0.1; r=r_0/N;
V=prix_am_vect(x_0,N,gain_put); Nbre=1000; for j=1:Nbre do
Bin=simul_bin(N,p); tau(j)=temps_optimal_option(Bin,V,gain_put);
end endfunction;
function main_9() N=50; for x_0=[60,70,80,100,120] do
printf("x_0=%f: %f\n",x_0,compute_proba(x_0,N)); end endfunction
-
17.
- Tracer la frontière d’exercice en fonction du temps.
function s=frontiere(V)
N=size(V); N=N(1)-1; s=0; for n=0:N do for j=[0:n] do x=x_0*u^j*d^(n-j);
if V(n+1,j+1) > gain_put(x) then s(n+1)=x_0*u^(j-1)*d^(n-j+1);break;
end; end end; endfunction function main_10()
N=1000; r_0=0.05;r=r_0/N; sigma=0.3; K=100;x_0=70;
p=1/2;d=1-sigma/sqrt(N);u=1+sigma/sqrt(N); V=prix_am_vect(x_0,N,gain_put);
front=frontiere(V); plot2d(1:size(front,'*'),front); endfunction;
2 Un problème de recrutement
On reçoit, consécutivement, N candidats à un poste. Les circonstances m’imposent de décider
tout de suite du recrutement (soit on recrute la personne que l’on vient de recevoir, soit on la
refuse définitivement). On cherche à maximiser la proabilité de recruter le meilleur candidat.
Quelle est la meilleure stratégie ?
On a vu en cours que l’on peut se ramener à (S1,…,SN) est une suite de variables aléatoires
indépendantes de Bernouilli 1∕n, qui est une chaîne de Markov sur l’espace E = {0, 1}, non
homogène, de matrice de transition, dépendant du temps, Pn
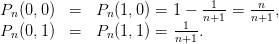
On chercher à maximiser P(τ est le meilleur) = E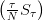 parmi tous les temps d’arrêt.
parmi tous les temps d’arrêt.
-
1.
- Ecrire un programme Scicoslab qui calcule la solution (u(n, 0 ou 1), 0 ≤ n ≤ N)
de l’équation de programmation dynamique donnée par (voir cours)
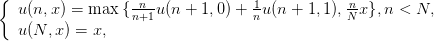
On calcule (u(n,{0, 1}), 0 ≤ n ≤ N) à l’aide de l’équation de programmation dynamique.
On désigne l’“obstacle” par (f(n,{0, 1}), 0 ≤ n ≤ N). Notez que f(n, 0) = 0 et
f(n, 1) = n∕N.
function u=compute_u(N) u=zeros(N,2); u(N,:)=[0,1];
for n=[N-1:-1:1] do temp=(n/(n+1))*u(n+1,1)+(1/(n+1))*u(n+1,2);
u(n,:)=[temp,max(temp,n/N)];
end; endfunction;
-
2.
- Tracer les courbes u(n, 0), u(n, 1) ainsi que “l’obstacle”
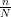 .
.
function main_11() N=1000; obstacle=[1:N]/N; u=compute_u(N);
plot2d(1:N,obstacle,style = 2); plot2d(1:N,u(:,2),style = 3);
plot2d(1:N,u(:,1),style = 4); endfunction
-
3.
- Interprétez u(0, 1) comme la probabilité de choisir le meilleur candidat avec une stratégie
optimale ? Tracer la courbe N donne
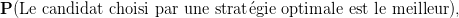
pour N = 10, 25, 50, 100, 250, 500, 1000. Vérifier numériquement qu’elle converge vers
1∕e ≈ 37%.
function main_12()
i=0; courbe=0;
valeurs=[10,25,50,100,250,500,1000]; for N=valeurs do u=compute_u(N);
i=i+1;courbe(i)=u(1,2); end plot2d(valeurs,courbe) endfunction
-
4.
- Vérifier que l’on a u(n, 0) > 0 pour tout n < N et donc, que 0 = f(n, 0) ⁄= u(n, 0). Par
ailleurs, on a bien sûr, u(N, 0) = 0 = f(N, 0). Comme le temps d’arret optimal τ est
donné par
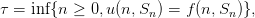
en déduire qu’il sera toujours postérieur à τmin, le premier temps où u(n, 1) = f(n, 1) = n∕N,
(puisque u(n, 0) > 0 = f(n, 0), sauf lorsque n = N) et que c’est la premier instant après
τmin pour lequel Sn = 1, si n < N.
Il découle de ce qui précéde qu’un temps d’arrêt optimal est donné par le
premier instant après nmin (nmin compris) où Sn = 1 (ou encore Rn = 1, c’est
à dire le premier instant où le nouvel arrivant est meilleur que ceux qui l’on
précédé).
Ecrire un algorithme de calcul de ce temps τmin.
function res=temps_min(N)
epsilon=10*%eps; u=compute_u(N); for n=[1:N] do
if (abs(u(n,2)-(n/N)) < epsilon) then break; end end res=n; endfunction
Vérifier par simulation que le temps (déterministe) τmin “vaut environ” N∕e pour N
grand. On peut le démontrer sans trop de difficulté à l’aide de la série harmonique.
function main_13()
Taille=1000; x=0; for N=[1:Taille] do x(N)=temps_min(N)/N;
end x=x-1/exp(1); nb=size(x,'*'); plot2d(1:nb,x); endfunction
-
5.
- Ecrire une fonction qui calcule la suite des rangs d’insertion (R dans le cours) d’une
permutation et une fonction qui calcule la permutation définie par ses rangs d’insertion
successifs.
function R=Omega2R(omega)
R=zeros(1,length(omega)); for n=[1:length(omega)] do
y=gsort(omega(1:n),'g','i');
R(n)=find(omega(n)==y); end endfunction function omega=R2Omega(R)
N=length(R); temp=zeros(1,N); for n=[1:N] do
temp=[temp(1:R(n)-1),n,temp(R(n):n-1)]; end;
for n=[1:N] do omega(temp(n))=n;end;
endfunction function main_14()
N=10; omega=grand(1,'prm',[1:N]')';
R=Omega2R(omega); and(R2Omega(R)==omega) endfunction
-
6.
- Vérifier par simulation que la probabilité d’obtenir le meilleur candidat, lorsque
l’on utilise la stratégie optimale, est de l’ordre de 1∕e ≈ 37%. Ce qui n’est
pas génial, mais c’est le mieux que l’on puisse faire (sans connaitre l’avenir!).
function n=temps_optimal(omega,tau_min)
S=(Omega2R(omega)==1);
for n=[tau_min:N] do
end
endfunction
On teste dans un cas particulier.
function main_15()
N=100; Taille=10000;
tau_min=temps_min(N); ss=0; for i=[1:Taille] do
omega=grand(1,'prm',[1:N]'); tirages(i)=temps_optimal(omega,tau_min);
if (omega(tirages(i))==1) then ss=ss+1;end;
end proba=ss/Taille; printf("probabilité d''obtenir le meilleur: %.3f\n",proba);
endfunction
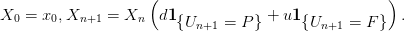
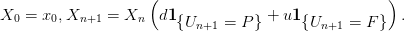
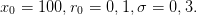
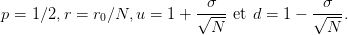
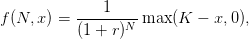
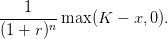
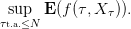
![( [ ]
|{ v(n,x) = max pv(n-+-1,xu-)+-(1−-p)v(n-+-1,xd),(K − x )+ ,n < N, x ∈ E
1+ r
|(
v(N, x) = (K − x)+,x ∈ E.](arret_scilab_ddi6x.png)
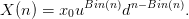
 cicosLab.
cicosLab.
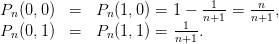
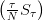 parmi tous les temps d’arrêt.
parmi tous les temps d’arrêt.
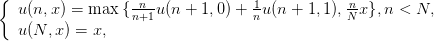
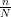 .
.