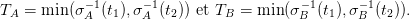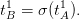Le but de ce TP est de vous montrer comment utiliser un environnement dédié au calcul
numérique comme ScicosLab/NSP/Scilab/MatLab/Octave/Julia dans un contexte
probabiliste. Ce type de langages est particulièrement adapté à un ingénieur souhaitant
prototyper son travail rapidement, souvent (mais pas toujours) en sacrifiant le temps
de calcul (celui de la machine) au bénéfice du temps passé à programmer (le votre)
.
Dans la suite du cours nous utiliserons Scilab pour concrétiser les notions que nous allons
introduire.
Aujourd’hui, nous allons illustrer la démarche par la traitement d’une question que nous avons
trouvé sur le site de la nsa. Dans la suite les expressions en couleursont (en principe) des liens html
cliquables.
La question à résoudre
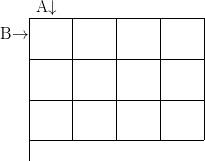
On place deux œufs “au hasard” dans une matrice p × q. On considère deux
joueurs (A et B). Le joueur A parcours la matrice en colonne, le joueur B en ligne.
Le gagnant est celui qui atteint le premier l’un des deux œufs. La question est
de savoir si ce jeu est équitable (i.e. les deux joueurs ont ils la même probabilité
de gagner ?) et de déterminer, si ce n’est pas le cas, lequel a un avantage.
On trouvera la réponse à cette question lorsque p = 3 et q = 4 sur le site de la NSA. Nous verrons que
l’on peut répondre très simplement à ces questions à l’aide de Scilab. Les réponses dépendent des
valeurs de p et q de façon surprenante : elles sont différentes pour (p = 3,q = 4), (p = 4,q = 4) et
(p = 4,q = 5) !
1 Installation de Scilab , rappels, exemples élémentaires.
Les codes qui suivent on été testés avec Scicoslab ou NSP. Il est probable qu’ils fonctionnerons
avec peu (ou pas) de modifications dans Scilab, mais nous vous conseillons d’installer Scilab sur
votre machine personnelle pour ne pas avoir de problèmes.
Installation et principes de base
Installation
Vous pouvez installer ScicosLab à partir de la page http://www.scicoslab.org/ sur la plupart des
architectures existantes (MacOS, Windows, Linux). Pour installer NSP, il faut utiliser sur la page
dédiée à NSP. Une version corrigée des codes qui suivent sera disponible à la fin du
TP.
Ouvrir une fenêtre Scilab
Pour ces travaux pratiques d’introduction à Scilab, il vous faut lancer le logiciel Scilab et disposer
ainsi d’une fenêtre permettant de saisir et d’exécuter des instructions.
Taper des instructions Scilab
Une ligne de commande Scilab est précédée du signe -->. Pour commencer, il vous suffit de les
recopier ou de les saisir par copier-coller (sans -->) pour les exécuter immédiatement dans la
fenêtre Scilab.
Commentaires
Toute ligne débutant par // est une ligne de commentaires.
Chercher de l’information
Lorsque l’on ne sait pas bien ce que fait une fonction.
Scalaires, vecteurs, matrices
scalaires
-->5 // en tapant le chiffre 5, Scilab attribue la valeur 5 à la variable ans
// (pour answer) -->ans^2 // ans élevé au carré donne 25 -->abs(-5)
// valeur absolue -->m=10^6 -->sqrt(m) // racine carrée -->y=%e -->log(y)
// %e est la constante e -->sin(%pi) // noter que le résultat n'est pas exactement zéro
-->1+%eps // %eps est la précision : 1+%eps/2 est indistinguable de 1
-->1+%eps/2==1 // est vrai ! -->1+%eps==1 // est faux.
vecteurs
-->v=[3.8,-4,%pi/6] -->size(v) // dimensions de v : 1 ligne et 3 colonnes -->w=v'
// transposition -->x=[1,2]; y=[3,4,5] -->z=[x,y]; // construction d'un vecteur par blocs
-->t=[4:9] // vecteur des réels entre 4 et 9 par pas de 1 (pas implicite) -->t=[4:1:9]
// vecteur des réels entre 4 et 9 par pas de 1 (pas explicite) -->t=[0:0.1:1]
// vecteur des réels entre 0 et 1 par pas de 0.1 -->u=sqrt(2)*[1:2:8]' -->size(u) -->t=rand(1,5)
// un vecteur à 1 ligne et 5 colonnes // et contenant des nombres au hasard dans [0,1]
matrices
-->[1,2;3,4] -->[11,12,13,14,15,16,17,18,19;21,22,23,24,25,...
-->26,27,28,29;31,32,33,34,35,36,37,38,39] // dans une instruction trop longue pour tenir dans une ligne,
// mettre ... avant de passer à la ligne -->diag([5 4 3]) // matrice diagonale
-->eye(6,6) // des 1 sur la diagonale -->B=eye(6,7) -->A=ones(3,7)
-->C=[A;(-6)*B] -->D=zeros(2,5) -->E=rand(D) -->rand(2,5)
Question 1.
- Construire une matrice (4,9) (à 4 lignes et 9 colonnes) dont la première ligne est
formée de 1, et dont tous les autres termes sont nuls.
- Construire une matrice (3,5) dont la première colonne est formée de 2, la deuxième
colonne des entiers de 1 à 3, et le reste de -1.
M=A_REMPLACER M=A_REMPLACER
Opérations vectorielles usuelles
fonctions (à arguments vectoriels)
-->u=2*%pi*rand() // un nombre au hasard dans [0,2*pi] -->w=[cos(u) sin(u)]
-->norm(w) // norme classique |$L^2$| -->norm(w,1) // norme |$L^1$| -->t=[0:%pi/2:2*%pi]
-->v=sin(t) -->[m,k]=max(v) // la valeur maximale des éléments du vecteur v est m
// et elle est atteinte pour l'élément d'indice k : m=v(k) -->[m,k]=min(v)
-->sign(v) // signe 1 (+) ou -1 (-) et sign(0)=0
opérations logiques
-->1==0 // la réponse à l'assertion ``1 égale 0'' est F false
-->1~=0 // la réponse à l'assertion ``1 différent de 0'' est F false
-->1==0 & 1~=0 // et : la réponse est F false -->1==0 | 1~=0 // ou : la réponse est T true
-->t=[0:%pi/2:2*%pi] -->v=sin(t) -->v>0 // renvoie un vecteur de T (true) ou F (false) selon que
// l'élément correspondant de v est ou non >0 -->v>=0 // convertit les T et F en 1 et 0
-->v(v>=0) // extrait les élément positifs ou nuls de v
addition
-->w=1:9 -->sum(w) // somme de tous les éléments de w -->cumsum(w)
// vecteur donnant les sommes cumulées
-->A=rand(2,3) -->B=sin(A) -->A+B
-->G=[ones(1,4); 2*ones(1,4)] -->sum(G,'c')
// somme sur les lignes : le résultat est un vecteur colonne ('c' pour column)
-->sum(G,'r') // somme sur les colonnes : le résultat est un vecteur ligne ('r' pour row)
transposition
multiplication
-->A'*A -->A*A' -->C=rand(2,3) -->A'*C
extraction d’éléments d’un vecteur
-->w=1:2:9 -->w(2) -->w($) // dernier élément -->w($-1) // avant-dernier élément
extraction de sous-matrices
-->E=[11:19;21:29;31:39;41:49;51:59;61:69] -->E(1,1) // l'élément de la ligne 1 colonne 1
-->E(3,4) // l'élément de la ligne 3 colonne 4 -->E(1,:) // la ligne 1
-->E(:,5) // la colonne 5 -->E(2:4,:) // la sous-matrice formée des lignes allant de 2 à 4
-->E(2:3,7:9) // la sous-matrice formée des éléments appartenant
// aux lignes allant de 2 à 3 et aux colonnes de 7 à 9
-->E([1,3,5],[2,4,6,8]) // la sous-matrice formée des éléments appartenant
// aux lignes 1 3 5 et aux colonnes 2 4 6 8 -->E(:,$) // dernière colonne
-->E(:,$-1) // avant-dernière colonne -->E(2:$,:) // les lignes de la deuxième à la dernière
-->E(2:($-1),:) // les lignes de la deuxième à l'avant-dernière
autres fonctions
-->A=int(20*rand(1,10)) // partie entière -->[sa,ia]=gsort(A)
// tri : sa est le résultat du tri, ia les indices correspondants
multiplication terme à terme
-->x=[1 2 3] -->x.*x -->y=[-6 12 8] -->x.*y -->A=rand(2,3); -->B=ones(2,3); -->A.*B
division terme à terme
-->x=[1 2 3] -->y=1 ./x // un blanc suit le 1, car sinon 1. serait interprété en 1.0 et
// l'opération serait / (résolution de système linéaire) -->x.*y
-->A=rand(2,3); -->B=rand(A); -->A./B
puissance terme à terme
-->x=[1 2 3] -->y=x.^2 -->z=x.^[5 10 -2] -->A=rand(2,3); -->A.^3 -->B=rand(A); -->A.^B
2 Étude de la question posée par une méthode de Monte-Carlo
On commence par traiter la question par simulation. On suppose (ce qui est implicite dans la
formulation du problème) que les 2 œufs sont placés, indépendamment, uniformément sur les p×q
cases de la matrice. Il peut donc arriver que les 2 œufs soient au même endroit (à vrai dire le
problème ne précise pas ce détail), mais on verra que cela n’a pas d’impact sur la réponse à la
question posée.
Éléments de syntaxe
Quelques compléments sur la syntaxe qui seront utiles.
Définir une fonction
function res=f(x) res=x*x*x; endfunction -->f(4) // = 64
Une fonction peut renvoyer un vecteur (bien sûr).
function [a,b,c,d]=g(x) a=x;b=x*x;c=x*x*x;d=1; endfunction
-->[x,y,z,t]=g(4) // x=4 y=16 z=64 t=1
Boucle while
U=2.5; i=0;// calcule le plus petit entier > U while i <= U i = i + 1; end
La fonction grand
La fonction X=grand(m, n, dist_type [,p1,...,pk]) permet de simuler un grand
nombre de loi de variables aléatoires en spécifiant dist_type (help grand pour les
détails).
U=grand(1,1,'unf',0,1);// tire *une* v.a. de loi uniforme sur [0,1]
U=grand(1,3,'unf',0,1);// tire un vecteur 1x3 de v.a. de loi uniforme
// sur [0,1] : U(1), U(2), U(3)
Simulation d’une loi discrète
On cherche à tirer au hasard selon la loi d’une variable aléatoire discrète N
P = (P(k), 1 ≤ k ≤ N).
La primitive grand qui simule pas mal de lois de variables aléatoires (mais pas la loi discrète !).
Ce qui nous donne l’occasion de faire une premier exercice de Scicoslab.
Voici une première version itérative (comme on l’écrirait en C).
function res=rand_disc_iter(P)
U=grand(1,1,'unf',0,1);
Q=0;i=0; while Q <= U do
i=i+1; Q=Q+A_REMPLACER; end res=i;
endfunction; p=10; P=ones(1,p)/p; for i=1:1000 do X(i)=rand_disc_iter(P);end;
mean(X), v=variance(X),
Par soucis d’efficacité, on cherche souvent à “éviter les boucles” à l’aide de commandes
vectorielles. Avant d’écrire une version vectorielle du programme précédent, introduisons quelques
primitives adaptées.
Éléments de syntaxe
max
-->X=[2,7,8]; -->max(X) // = 8
Primitives booléennes
Le test booléens fonctionnent sur les types vectoriels. C’est commode.
-->2>7 // = | F | -->X > 7 // = | F F T | -->cumsum(X) > 7 // = | F T T |
find
Retourne les indices “vrai” d’un vecteur de booléen.
-->find(cumsum(X) > 7) // = | 2 3 | -->X(find(X > 7)) // = | 8 |
-->X(find(cumsum(X) > 7)) // = | 7 8 |
La boucle for
Les boucles sont particulièrement adaptées aux vecteurs.
X=1:10;// 1,2,3, .... , 10 Z=0; for i=1:length(X) do Z = Z + X(i);
end; -->Z // = | 55 | S=0;Z=0; for i=1:length(X) do Z = Z + X(i);
S(i)=Z; end; -->S // = |1 3 6 10 15 21 28 36 45 55 |
Affichage
Si vous connaissez C, c’est facile, c’est la même chose.
-->printf("%d+%d ?=? %d\n",1,1,2); // Output: 1+1 ?=? 2
-->printf("%d+%d ?=? %d\n",1,2,2); // Output: 1+2 ?=? 2
Simulation “vectorielle” d’une loi discrète
On peut écrire une version de la simulation d’une loi discrète sans boucle.
function res=rand_disc(P) // P est une loi discrète représenté par une vecteur *ligne*
// Version "sans boucle" Q=[0,cumsum(P)];// On calcule la fonction de répartition de la loi
// |$Q(i)=\P(N\leq i-1)$|, |$i-1$| car |$Q(1)=0$|.
U=grand(1,1,'unf',0,1);// On tire selon une loi uniforme entre 0 et 1
res=max(A_REMPLACER);// res=le plus grand des |$i$| tel que |$U \geq Q(i) = \P(N\leq i-1)$|
endfunction;
Un premier test pour vérifier que ça marche.
function test_0()
p=3; P=ones(1,p)/p; N=1000;
for i=1:N do X(i)=rand_disc(P);
printf("%d.",X(i)); end printf("\n"); endfunction
Simulation des temps d’atteinte
On tire le premier œuf en (U1,V 1), U1 (l’indice de ligne) et V 1 (l’indice de colonne) étant
indépendantes, de loi uniforme respectivement sur {1,…,p} et {1,…,q}. Si le premier œuf se
trouve en (U1,V 1), le temps d’atteinte de cet œuf par A (parcours en colonne) est donné
par
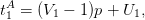
et, pour B (parcours en ligne), par
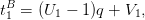
avec des formules identiques pour le deuxième œuf :

U2 et V 2 étant indépendantes, toujours de lois uniformes, indépendantes du couple
(U1,V 1).
Noter que l’on peut calculer la loi (commune) de t1A, t
1B, t
2A, t
2B (loi uniforme sur
{1,…,p × q}) et montrer que t1A s’obtient comme une fonction déterministe de t
1B (voir
complément 1).
Avec ces éléments, il est facile d’écrire une fonction qui réalise le tirage des deux œufs
dans la matrice et d’en déduire les temps que mettent A et B pour trouver le premier
œuf.
function [T_A,T_B]=random_times(p,q)
P=ones(1,p)/p;
Q=ones(1,q)/q; i_1=rand_disc(P);j_1=rand_disc(Q);
i_2=rand_disc(P);j_2=rand_disc(Q);
t_1_A=A_REMPLACER t_2_A=A_REMPLACER T_A=min(t_1_A,t_2_A);
t_1_B=A_REMPLACER; t_2_B=A_REMPLACER; T_B=min(t_1_B,t_2_B); endfunction;
Il ne reste plus qu’à faire suffisamment de tirages pour répondre (en partie) à la question
posée.
La syntaxe du if ... then ... elseif ... else ... end
Le elseif et le else sont optionnels.
x=12; if x==3 then printf("Bravo, vous avez gagné 2 euros.\n"); elseif x==4 then
printf("Bravo, vous avez gagné 1 euros.\n"); else printf("Vous avez perdu, sorry.\n"); end;
function qui_gagne_MC(p,q,N) statA=0;statB=0; for i=[1:N] do
[T_A,T_B]=random_times(p,q); if A_REMPLACER then
A_REMPLACER elseif A_REMPLACER then A_REMPLACER
end; end; erreur=1/sqrt(N); pA=statA/N;pB=statB/N;
printf("pA=%.3f+-%.3f, pB=%.3f+-%.3f\n",statA/N,erreur,statB/N,erreur);
if (pA+erreur < pB-erreur) then printf("p=%d,q=%d : ",p,q);
printf("Il est très probable que B gagne en moyenne.\n"); elseif (pA-erreur > pB+erreur) then
printf("p=%d,q=%d : ",p,q); printf("Il est très probable que A gagne en moyenne.\n");
else printf("p=%d,q=%d, N=%d : On ne peut pas conclure: ",p,q,N);
printf("il faut augmenter le nombre de tirages N.\n"); end endfunction;
function test_1() N=100000; qui_gagne_MC(2,3,N); qui_gagne_MC(3,4,N);
qui_gagne_MC(4,5,N); qui_gagne_MC(4,4,N); endfunction;
Noter que le théorème de la limite centrale permet (exercice !) de montrer que l’erreur “probable
maximale” est de l’ordre de 1∕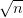 (C’est ce même résultat qui permet d’évaluer approximativement
l’erreur d’un sondage d’opinion).
(C’est ce même résultat qui permet d’évaluer approximativement
l’erreur d’un sondage d’opinion).
Dans le cas p = 2, q = 3 on arrive assez facilement (N = 10000 suffit largement) à se
convaincre que B gagne en moyenne. C’est plus difficile pour (p = 3,q = 4) (N = 100000
convient). Ça devient délicat pour (p = 4,q = 5) (il faut prendre N ≈ 1000000 pour conclure
que c’est A qui gagne). Dans les cas où p = q (où l’on peut prouver qu’il y a égalité
des probabilités, voir le complément 3), une méthode de simulation ne sera jamais
concluante.
Il nous faut une méthode exacte de calcul de ces probabilités. C’est ce que nous allons faire
maintenant.
3 Un calcul exact par énumération exhaustive
L’espace de probabilité Ω étant fini, il suffit d’énumérer Ω pour calculer la probabilité : on génère
toutes les valeurs possibles pour les positions des œufs (i1,j1) et (i2,j2) (tous ces couples (de
couples !) sont équiprobables), on calcule TA et TB et l’on fait des stats sur celui qui gagne.
On en profite pour calculer la loi du couple (TA,TB) et pour vérifier que les lois de
TA et TB sont identiques (voir le complément 2 si vous souhaitez une preuve de ce
fait).
Attendu : ones, zeros, initialiser les matrices avant les boucles sum(.,opt) et norm
function H_AB=qui_gagne_elem(p,q) Ascore=0;Bscore=0;nbre_cas_egalite=0;
valeurs_TAB=zeros(2,1);nAB=0;
for i_1=1:p do for j_1=1:q do for i_2=1:p do
for j_2=1:q do T_A=min((j_1-1)*p+i_1,(j_2-1)*p+i_2);
T_B=min((i_1-1)*q+j_1,(i_2-1)*q+j_2); if T_A > T_B then
Bscore=Bscore+1; elseif T_A < T_B then Ascore=Ascore+1;
else nbre_cas_egalite=nbre_cas_egalite+1;
end
nAB=nAB+1;valeurs_TAB(:,nAB)=[T_A;T_B]; end end end
end
H_AB=histo(p*q,valeurs_TAB);
H_A=A_REMPLACER;
H_B=A_REMPLACER; if norm(H_A-H_B) >= 1.E-7 then
printf("Warning: les lois marginales doivent être égales.\n"); end
printf('p=%d, q=%d, ',p,q);
report(p*q,Ascore,Bscore,nbre_cas_egalite,H_AB); endfunction;
Les fonctions histo et report. La première calcule un histogramme à partir de valeurs. report
imprime quelques informations à l’écran.
function H_AB=histo(v_max,samples)
H_AB=0 nbre=size(samples);nbre=nbre(2); for k=1:v_max do
for l=1:v_max do
H_AB(k,l)=length(find((samples(1,:)==k) & (samples(2,:)==l))) ./nbre;
end; end; endfunction;
function report(Taille,Ascore,Bscore,nbre_cas_egalite,H_AB)
out_fmt="Taille=%d, diff=%d, egalite=%d : "; if (Bscore > Ascore) then
out_fmt=out_fmt+"C''est B qui gagne\n"; elseif (Ascore > Bscore) then
out_fmt=out_fmt+"C''est A qui gagne\n"; else out_fmt=out_fmt+"Egalité\n";end
printf(out_fmt,Taille,Bscore-Ascore,nbre_cas_egalite); endfunction;
function test_2() p=2;q=p+1; loi_TAB=qui_gagne_elem(p,q);
for p=[2:9] do qui_gagne_elem(p,p+1);end; for p=[2:8] do qui_gagne_elem(p,p+2);end;
for p=[2:7] do qui_gagne_elem(p,p+3);end; endfunction;
4 Une version plus rapide du code
Les langages de type Scilab, MathLab sont relativement lents, tout particulièrement lorsque l’on
utilise des boucles, ce qui est la cas ici.
On peut accélérer sensiblement les performances de l’algorithme en supprimant les boucles à
l’aide de fonctions vectorielles.
On utilise des produits de Kronecker .*. de matrice A et B, où chaque terme Aij de A est
remplacé par la matrice AijB. Si A est de taille nA × mA et B est de taille nB × mB, A .*. B
est de taille nAnB × mAmA.
-->A=[1,2;2,4]; // | 1 2 | // | 2 4 | -->A .*. A // | 1 2 2 4 |
// | 2 4 4 8 | // | 2 4 4 8 | // | 4 8 8 16 |
Voici un exemple de ce que donne une réécriture efficace de la fonction qui_gagne_elem. Le gain
d’efficacité se fait au détriment de la lisibilité des codes et d’une utilisation mémoire qui peut être
importante.
function qui_gagne_optim(p,q) pq=p*q;
A=1:pq;A=matrix(A,p,-1);
B=A;B=matrix(B,q,-1);B=B';
O1=ones(1,pq) .*.(1:pq); O2=(1:pq) .*.ones(1,pq);
mA=min(A(O1),A(O2));
mB=min(B(O1),B(O2));
I=find(mA==mB);
nbre_cas_egalite=size(I,'*'); mA(I)=[];mB(I)=[];
[m,I]=min(mA,mB);
Ascore=length(find(I==1)); Bscore=length(find(I==2)); printf('p=%d, q=%d,',p,q);
report(p*q,Ascore,Bscore,nbre_cas_egalite,0); endfunction;
function test_6()
for p=[2:20] do qui_gagne_optim(p,p+1);end; for p=[2:20] do qui_gagne_optim(p,p+2);end;
for p=[2:20] do qui_gagne_optim(p,p+3);end; endfunction;
5 Compléments de probabilités
Ces compléments sont destinés aux élèves souhaitant avoir des clarifications et des
preuves concernant le problème posé. Sa lecture ne vous apprendra à programmer en
Scilab, elle est conseillé en révision du cours de probabilité de M. Alfonsi du premier
semestre.
Complément 1. Les temps aléatoires t1A et t1B suivent tous les deux une loi uniforme sur {1,…,p×q}.
En effet, si k est un nombre entier compris entre 0 et p × q − 1, il s’écrit de façon unique sous la forme
k = i1 × p + j1 avec i1 ∈{0,1,…,q − 1} et j1 ∈{0,1,…,p − 1}. On a donc :
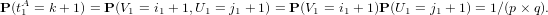
Ces temps ne sont pas indépendants, en fait t1B s’obtient par une permutation déterministe à partir de
t1A : il existe une permutation σ de {1,…,pq} telle que
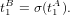
Il est facile de s’en convaincre, puisque à chaque case (i,j) correspond un temps d’atteinte diffèrent pour
chacun des joueurs : pour construite la permutation, il suffit donc de mettre en relation le temps mis par A
pour atteindre (i,j) avec le temps mis par B pour atteindre la même case. Voir page 21 pour un programme
qui calcule explicitement cette permutation.
On peut aussi voir que, lorsque l’on considère le jeu avec un seul œuf, on a toujours un problème équitable
(i.e. on a P(t1A < t1B) = P(t1B < t1A)). Pour s’en convaincre on écrit
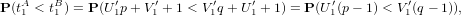
où U′1 = U1 − 1 suit une loi uniforme sur {0,…,q − 1} et V ′1 = V 1 − 1 suit une loi uniforme sur
{0,…,p − 1} et sont indépendants. Comme (U′1,V ′1) suit la même loi que (q − 1 − U′1,p − 1 − V ′1), on
a
Complément 2. Pour montrer que TA et TB suivent la même loi, on commence par remarquer qu’il
existe une permutation σ de {1,…,p × q} telle que tB1 = σ(tA1) et tB2 = σ(tA2) (elle est calculé plus tard,
mais c’est facile de s’en convaincre). Comme tA1 et tA2 suivent des lois uniformes sur {1,…,p × q}, c’est
aussi le cas de tB1 et tB2 (exercice). tB1 et tB2 sont indépendantes, puisque fonctions de variables aléatoires
indépendantes. Les couples (tA1,tA2) et (tB1,tB2) suivent donc la même loi et l’on conclut que TA et TB
ont même loi puisque

Il convient de noter que les temps aléatoires TA et TB ne sont pas indépendants. C’est d’ailleurs ce qui fait
l’intérêt de la question posée (Que se passerait-il si TA et TB étaient indépendants ?).
Complément 3. On peut montrer que si σ2 = Id, alors la loi du couple (TA,TB) est identique à celle
du couple (TB,TA). En effet on a :
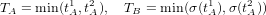
Donc, en utilisant le fait que la loi de (tA1,tA2) est identique à celle de (σ(tA1),σ(tA2)), on obtient :
Et lorsque σ2 = Id, on en déduit P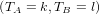 = P(TB = k,TA = l). Ceci permet d’en déduire (exercice
simple mais instructif) que
= P(TB = k,TA = l). Ceci permet d’en déduire (exercice
simple mais instructif) que
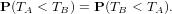
La relation σ2 = Id est vérifiée lorsque p = q (on peut le vérifier à l’aide du programme Scilab ou ...
le prouver si on est courageux). Ce qui prouve le résultat (attendu !) que lorsque p = q le jeux est
équilibré.
6 Étude à l’aide de permutations
On peut généraliser ce jeu à proposant aux deux joueurs de choisir une permutation σ d’un
ensemble fini 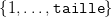 .
.
On tire alors au hasard indépendemment la place des deux objets entre 1 et taille. On note t1
la première variable aléatoire et t2 la deuxième. t1 et t2 sont supposées indépendantes et de loi
uniforme sur 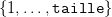 .
.
Le joueur A parcours les cases dans l’ordre σA(1),…,σA(taille) et B dans l’ordre
σB(1),…,σB(taille), ainsi
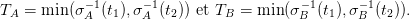
La question est de comparer P(TA < TB) et P(TB < TA). Le programme suivant répond à cette
question.
function H_AB=qui_gagne_permutation(taille,sigma_A_1,sigma_B_1) Ascore=0; Bscore=0;
nbre_cas_egalite=0; valeurs_TAB=zeros(2,taille); nAB=0;
for i_1=1:taille do for i_2=1:taille do T_A=min(sigma_A_1(i_1),sigma_A_1(i_2));
T_B=min(sigma_B_1(i_1),sigma_B_1(i_2)); if T_A > T_B then Bscore=Bscore+1;
elseif T_A < T_B then Ascore=Ascore+1; else
nbre_cas_egalite=nbre_cas_egalite+1; end nAB=nAB+1;valeurs_TAB(:,nAB)=[T_A;T_B];
end end H_AB=histo(taille,valeurs_TAB);
report(taille,Ascore,Bscore,nbre_cas_egalite,H_AB); endfunction;
Évidemment pour gagner il faut bien choisir sa permutation (ou avoir de la chance).
Voici une fragment qui permet de tester le programme précédent. Exécuter le plusieurs
fois et vérifier que l’on peut gagner ou perdre ou (parfois) être dans un cas d’égalité.
function test_3() taille=6;
sigma_A_1=grand(1,"prm",[1:taille]'); sigma_B_1=grand(1,"prm",[1:taille]');
H_AB=qui_gagne_permutation(taille,sigma_A_1,sigma_B_1) endfunction;
La permutation correspondant à la transposition d’un matrice
On peut expliciter la permutation de [1 : p×q] générée par la transposition d’une matrice p×q en
une matrice q × p. Plus précisément, on cherche la permutation qui permet d’exprimer le temps
d’atteinte du premier œuf par B tB1 en fonction du temps d’atteinte de ce même œuf par A,
tA1 :
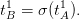
Cette permutation est facile à calculer : il suffit, pour tout (i,j) d’envoyer le temps d’atteinte de
A sur le temps d’atteinte de B.
function sigma=permutation(p,q)
sigma=0; for i=[1:p] do for j=[1:q] do t_1_A=(j-1)*p+i;
t_1_B=(i-1)*q+j; sigma(t_1_A)=t_1_B;
end end endfunction;
Noter que cette permutation σ permet de reformuler le problème initial puisque l’on s’intéresse
à la loi de du couple TA = min(tA1,t
A2) et T
B = min(tB1,t
B2) où t
A1,t
A2 sont indépendants de loi
uniforme sur [1 : p × q] et tB1 = σ(t
A1) et t
B2 = σ(t
A2). La permutation σ est le seul paramètre à
la question.
Le fragment suivant répond à la question initiale en utilisant σ.
function H_AB=qui_gagne_elem_variante(p,q) identite=1:p*q;
sigma=permutation(p,q); printf('p=%d, q=%d, ',p,q);
H_AB=qui_gagne_permutation(p*q,identite,sigma) endfunction;
On vérifie que la loi reste identique avec les deux méthodes proposées.
function test_5() p=4;q=6; H2=qui_gagne_elem(p,q);
H1=qui_gagne_elem_variante(p,q);
norm(H1-H2); endfunction;
On peut montrer (voir le complément 3 pour une preuve détaillée) que si σ2 = Id, la loi du
couple (TA,TB) est identique à celle du couple (TB,TA) (la loi du couple est symétrique), et donc
que P(TA > TB) = P(TA > TB) (on est dans un cas d’égalité). C’est en particulier le cas lorsque
p = q, ce qui n’est pas surprenant.
Une permutation qui permet de gagner à coup sûr
A partir d’une permutation σA choisie par A, B peut construire une permutation σB meilleure en
probabilité et ce quel que soit le choix de A ! ... et B peut aussi faire la même chose. Pour cela il
suffit de trouver un permutation σ0 meilleure que l’identité (il en existe toujours) et le choix
σB−1 = σ
0(σA−1) convient alors.
On peut choisir, par exemple, σ0 = [N; 1; 2; 3; 4; …; (N − 1)]. Mais il en existe d’autres.
function test_4() taille=6; sigma_A_1=grand(1,"prm",[1:taille]');
sigma_0=[taille,1:taille-1];
sigma_B_1=sigma_0(sigma_A_1); sigma_A_1'
H_AB=qui_gagne_permutation(taille,sigma_A_1,sigma_B_1); endfunction;
La permutation “zig-zag”
On peut aussi construire la permutation qui correspond au “zig-zag” (en colonne pour A et en
ligne pour B) et comparer avec le choix classique.
function t_A=temps_A_zig_zag(i,j,p,q)
if modulo(j,2)==0 then t_A=(j-1)*p+(p-i+1); else t_A=(j-1)*p+i; end endfunction;
function t_B=temps_B_zig_zag(i,j,p,q)
if modulo(i,2)==0 then t_B=(i-1)*q+(q-j+1); else t_B=(i-1)*q+j;
end endfunction; function sigma=permutation_zig_zag(p,q)
sigma=0; for i=[1:p] do
for j=[1:q] do t_1_A=temps_A_zig_zag(i,j,p,q); t_1_B=temps_B_zig_zag(i,j,p,q);
sigma(t_1_A)=t_1_B; end end endfunction;
On regarde l’effet du choix du zig-zag.
function H_AB=qui_gagne_elem_zz(p,q) identite=1:p*q;
sigma=permutation(p,q); printf('\ndirect, p=%d, q=%d, ',p,q);
H_AB=qui_gagne_permutation(p*q,identite,sigma) sigma=permutation_zig_zag(p,q);
printf('zigzag, p=%d, q=%d, ',p,q); H_AB=qui_gagne_permutation(p*q,identite,sigma)
endfunction; function test_7() for p=[2:9] do qui_gagne_elem_zz(p,p+1);end;
for p=[2:8] do qui_gagne_elem_zz(p,p+2);end; for p=[2:7] do qui_gagne_elem_zz(p,p+3);end;
endfunction;
function main() test_0() test_1() test_2() test_3() test_4()
test_5() test_6() test_7() endfunction
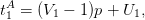
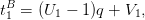

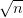 (C’est ce même résultat qui permet d’évaluer approximativement
l’erreur d’un sondage d’opinion).
(C’est ce même résultat qui permet d’évaluer approximativement
l’erreur d’un sondage d’opinion).
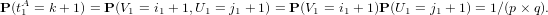
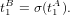
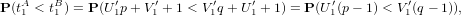
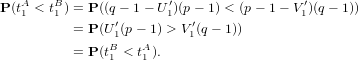

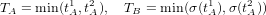
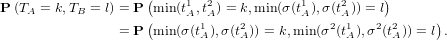
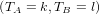
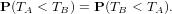
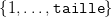 .
.
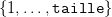 .
.