Le fichier source en Scilab correspondant à ce document est markowitz_scilab_ddi.sci. Il est
partiellement mais pas totalement corrigé. Les partie à compléter sont signalées par le préfixe
Il vous revient de changer ces lignes. Le correction complète sera markowitz_scilab_ddi_corrige.sci
accessible à la fin du TD.
Le fichier utils.sci définit certaines primitives (graphiques pour l’essentiel) utilisées par la
suite. Le télècharger et le sauvegarder sous le nom “utils.sci”. Il devra être accessible
par la suite dans votre directory de travail (qui s’obtient par “pwd” dans le shell de
Scicoslab).
Introduction
On considère d actifs dont les rendements sont donnés pas (R1,…,Rd). L’hypothèse de rendement
signifie que si on détient à l’instant 0 une quantité d’actif i de valeur V , la valeur de cette
même quantité d’actif à l’instant T (égal à T = 1 an par exemple) sera donnée par
V (1 + Ri).
On suppose de plus que ces rendements ont des caractéristiques de moyenne et de variance
connue. On note μ le vecteur des espérances μi = E(Ri) et Γ la matrice de variance covariance, où
Γij = Cov(Ri,Rj). On note σi2 = Var(X
i) = Γii.
1 Le cas à deux actifs risqués
On suppose que d = 2, que μ1 = 5% et μ2 = 15%, que σ1 = 10% et σ2 = 30% et ρ étant un
paramètre réel, Γ est donnée par
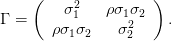
-
1.
- Que représente ρ ? A quelle condition sur ρ la matrice Γ est la matrice de covariance
d’un vecteur aléatoire ? Dans la suite, on prendra ρ = 0.
On constitue un portefeuille de valeur initiale X0 = 1 constitué d’une quantité x1
d’actif 1 et x2 d’actif 2 avec x1 ≥ 0, x2 ≥ 0 et X0 = x1 + x2 = 1 (i.e. on répartit 1E
entre le deux actifs risqués). On note XT la valeur de ce portefeuille en T
Vérifier que si le gain GT est défini par GT = XT − X0, E(GT ) = μ1x1 + μ2x2 =
μ2 + x1(μ1 − μ2) et Var(GT ) = x.Γx = σ12x
12 + σ
22(1 − x
1)2 + 2ρσ
1σ2x1(1 − x1).
-
2.
- Tracer les caractéristiques des actifs de base dans le plan moyenne,variance.
exec("utils.sci");
d=2; mu=[0.05,0.15];
rho=0.0; covariance=rho*ones(d,d)+(1-rho)*eye(d,d); sigma=[0.10,0.30];
Gamma=diag(sigma)*covariance*diag(sigma);
moyenne_actif=mu; std_actif=sigma;
rectangle=plot_actifs(moyenne_actif,std_actif);
-
3.
- Tracer la courbe x1 ∈ [0, 1] → (E(GT ),
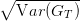 ).
).
Vérifier que l’on peut construire un portefeuille de même variance que l’actif 1 mais dont
l’espérance du rendement est supérieure à celle de cet actif. Est il rationnel d’investir dans
l’actif 1, si l’on cherche à minimiser son risque ?
Quel sont les portefeuilles dans lesquels il paraît rationnel d’investir ?
N=100; x_1=[0:1/N:1]; x=[x_1;1-x_1]; moyenne_x=0;std_x=0; for i=[1:N+1] do
current_x=x(:,i);
end; plot2d(std_x,moyenne_x,style = 1,rect = rectangle);
set_line(bleu,1);
-
4.
- Vérifier que l’on peut construire un portefeuille de variance minimum (et inférieure à celle de
l’actif de variance minimum). C’est un exemple de l’effet de diversification dans la théorie des
portefeuille.
[m,imin]=min(std_x);
plot2d(std_x(imin),moyenne_x(imin),rect = rectangle);
set_dot(vert,4);
-
5.
- Nous relaxons la condition x1 ≥ 0, x2 ≥ 0 tout en continuant à imposer x1 + x2 = 1 (la valeur
totale de notre investissement initial reste égale à 1). Nous allons faire varier x1 entre −10 et
0 (lorsque x1 est négatif, on emprunte une quantité |x1| d’actif 1, mais la valeur totale du
portefeuille doit toujours rester égale à 1).
Tracer la courbe x1 ∈ [−5, 0] → (E(GT ),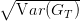 ). Vérifier que, si l’on accepte une
variance grande, on peut constituer des portefeuilles d’espérance aussi grande que souhaitée
(cet effet porte le nom d’effet de levier ou leverage effect). On comprend qu’il ne faille pas en
abuser !
). Vérifier que, si l’on accepte une
variance grande, on peut constituer des portefeuilles d’espérance aussi grande que souhaitée
(cet effet porte le nom d’effet de levier ou leverage effect). On comprend qu’il ne faille pas en
abuser !
moyenne_x=0;std_x=0;
N=1000;
x_1=[-5:A_COMPLETER:0];
x_2=A_COMPLETER; x=[x_1;x_2]; for i=[1:N+1] do current_x=x(:,i);
moyenne_x(i+1)=mu*current_x; std_x(i+1)=sqrt(current_x'*Gamma*current_x);
end; plot2d(std_x,moyenne_x,style = point,rect = rectangle);
set_line(vert,1);
-
6.
- Tracer la courbe x2 ∈ [−5, 0] → (E(GT ),
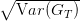 ). Vérifier que lorsque l’on emprunte
l’actif 2 (x2 négatif), l’on fait décroître l’espérance en augmentant la variance (ce qui est loin
d’être optimal !).
). Vérifier que lorsque l’on emprunte
l’actif 2 (x2 négatif), l’on fait décroître l’espérance en augmentant la variance (ce qui est loin
d’être optimal !).
moyenne_x=0;std_x=0;
N=1000;
x_2=[-5:A_COMPLETER:0]; x_1=A_COMPLETER; x=[x_1;x_2]; for i=[1:N+1] do current_x=x(:,i);
moyenne_x(i+1)=mu*current_x; std_x(i+1)=sqrt(current_x'*Gamma*current_x);
end; plot2d(std_x,moyenne_x,style = point,rect = rectangle);
set_line(rouge,1);
-
7.
- Recommencer l’expérience précédente avec des valeurs de ρ non nulle. Prendre par
exemple
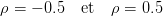
Que peut représenter ces valeurs de ρ ?
rho=0.5;
covariance=rho*ones(d,d)+(1-rho)*eye(d,d); Gamma=diag(sigma)*covariance*diag(sigma);
-
8.
- Nous allons introduire un nouvel actif, l’actif sans risque, qui comme son nom le suggère aura
un rendement de variance nulle (ce qui implique que ce rendement n’est pas aléatoire). On
supposera que ce rendement déterministe est inférieur à tous les rendements moyens des
actifs risqués (pourquoi est-ce une hypothèse raisonnable ?). On prendra, ici, ce rendement
égal à 0.
On constitue des portefeuilles avec les 3 actifs (1 non risqué, 2 risqués) en tirant au hasard
des coefficients (x1,x2,x3) dans le simplexe 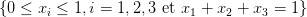 . La
fonction simplexe(d) figurant dans utils.sci pour d = 3 fait ce travail.
. La
fonction simplexe(d) figurant dans utils.sci pour d = 3 fait ce travail.
Matérialiser, en tirant un grand nombre points au hasard, la nouvelle frontière efficiente.
Vérifier que :
- la nouvelle frontière efficiente étend l’ancienne par de nouveaux points ”non
dominés” entre l’actif sans risque et un portefeuille tangent à l’ancienne frontière
P.
- que la variance reste bornée par la variance la plus grande (tant que l’on ne fait
pas d’emprunt).
r0=0; mu=[r0,mu];
moyenne_actif=mu;
std_actif=sqrt(diag(Gamma));
plot2d(std_actif,moyenne_actif,style = 1,rect = rectangle); set_dot(noir,4);
N=1000;
moyenne_x=0;std_x=0; for i=[1:N] do x=simplexe(d+1);
moyenne_x(i)=mu*x; std_x(i)=sqrt(x'*Gamma*x); end;
plot2d(std_x,moyenne_x,style = -1,rect = rectangle); set_dot(bleuclair,2);
Commentaire :
On obtient de nouveaux points ”non dominés” entre l’actif sans risque et un portefeuille
tangent. La variance reste bornée par la variance de l’actifs de plus grande variance tant que
l’on n’emprunte pas.
-
9.
- On va identifier un portefeuille particulier P, le “portefeuille de marché”. P est le
portefeuille correspondant au point de tangence de la droite passant par l’actif sans
risque et de l’ensemble de tous les portefeuilles a coefficients positifs de la question
précédente.
Le point P est caractérisé par le fait qu’il maximise la pente des droites reliant le point
(σ0 = 0,r0 = 0) et les points correspondants à des portefeuilles y ne faisant pas intervenir
d’actif sans risque.
Toujours en procédant par simulation dans le simplexe, calculer P (en fait une
approximation de P).
Vérifier que le portefeuille P fait intervenir les 2 actifs risqués.
N=1000; moyenne_y=0;std_y=0;
for i=[1:N] do
moyenne_y(i)=mu*y; std_y(i)=sqrt(y'*Gamma*y); end;
r0=mu(1);
sigma0=0; pente=(moyenne_y-r0) ./(std_y-sigma0);
[lambda,imax]=max(pente); x_P=moyenne_y(imax);
sigma_P=std_y(imax); plot2d(sigma_P,x_P,style = 1,rect = rectangle);
set_dot(vert,4);
plot2d([sigma0,sigma_P],[r0,x_P],style = 1,rect = rectangle); set_line(vert,2);
lambda=(x_P-r0)/(sigma_P-sigma0); sigma=2.0;
x=r0+lambda*(sigma-sigma0); plot2d([sigma0,sigma],[r0,x],rect = rectangle); set_line(vert,2);
-
10.
- On autorise la détention d’une quantité de signe arbitraire d’actif sans risque (cela
correspond soit à un emprunt, soit à un placement). Pour cela on vous suggère de tirer la
quantité d’actif sans risque x0 entre [−4, 1] (on peut emprunter jusqu’à 4 fois ce que l’on
possède). Puis on tire, les quantités d’actifs risqués uniformément sur le simplexe
{x1 + x2 = 1 − x0}.
Tirer un grand nombre de portefeuille, calculer leurs moyennes et écarts-type, les tracer sur
la figure.
N=1000; moyenne_x=0;variance_x=0;
for i=[1:N] do
x_0=grand(1,1,'unf',-4,1);
s=simplexe(d);
moyenne_x(i)=mu*x;
variance_x(i)=sqrt(x'*Gamma*x); end;
plot2d(variance_x,moyenne_x,style = -2,rect = rectangle); set_dot(mauve,2);
Vérifier que :
- l’on obtient de nouveaux points “non dominés” au delà du portefeuille tangent.
- le rendement (mais aussi la variance) peut devenir aussi grand que souhaité : effet
de levier.
- un emprunt permet de construire des portefeuilles dont la moyenne des rendements
est plus élevée à variance égale : emprunter permet d’augmenter le rendement.
- l’emprunt permet de construire des portefeuilles de même moyenne mais de variance
inférieure : emprunter permet de réduire le risque. Il existe en particulier un
portefeuille dont la variance est égale à celle de l’actif 2 (l’actif de rendement
maximum) mais de rendement supérieur.
- le seul point de la “frontière sans emprunt” qui n’est pas dominé par un point de
la “frontière avec emprunt” est le point P : si l’on ne souhaite pas emprunter, le
seul point rationnel est P.
- le portefeuille P fait intervenir l’ensemble des actifs de base risqués (en dehors des
actifs de base dominés par d’autres actifs de base).
-
11.
- On peut aussi autoriser la détention d’une quantité de signe arbitraire de l’un
quelconque des actifs. Pour cela on tire “au hasard” les coefficients (x1,x2,x3) du
portefeuille sans imposer de condition de positivité. C’est un peut plus délicat
puisque le support des tirages n’est plus compact et la loi uniforme n’a pas de sens.
La fonction arbitraire(d,alpha) figurant dans utils.sci pour d = 3 fait ce
travail. alpha est un paramètre réel à régler (alpha égal à 1 convient dans ce
cas).
Tirer un grand nombre de portefeuille, calculer leurs moyennes et écarts-type, les tracer. On
constate que tous ces nouveaux portefeuilles restent en dessous de la droite de marché.
d=3; N=1000; moyenne_x=0;variance_x=0; for i=[1:N] do x=arbitraire(d); moyenne_x(i)=mu*x;
variance_x(i)=sqrt(x'*Gamma*x); end;
plot2d(variance_x,moyenne_x,style = -2,rect = rectangle); set_dot(mauve,2);
2 Le cas d’un nombre d’actifs risqués arbitraire
Lorsque d > 2 les phénomènes sont identiques mais moins explicites. On peut recommencer ce qui
précède mais il faudra généraliser le choix de la matrice de variance covariance et procéder par
simulation dans tous les cas. Notez que les programmes fournis en correction fonctionnent en
dimension arbitraire (sauf aux questions 1 et 2).
A titre indicatif voici un exemple du cas d = 3.
-
1.
- Choix des actifs de base.
d=3;rho=0.0;
min_esp=0.05;max_esp=0.15; mu=[min_esp:(max_esp-min_esp)/(d-1):max_esp];
covariance=rho*ones(d,d)+(1-rho)*eye(d,d);
min_sigma=0.1;max_sigma=0.3; sigma=[min_sigma:(max_sigma-min_sigma)/(d-1):max_sigma];
Gamma=diag(sigma)*covariance*diag(sigma);
moyenne_actif=mu;
std_actif=sqrt(diag(Gamma));
rectangle=plot_actifs(moyenne_actif,std_actif);
-
2.
- Tirages des portefeuilles à coefficients positifs.
N=1000; moyenne_x=0;std_x=0; for i=[1:N] do
x=simplexe(d); moyenne_x(i)=mu*x; std_x(i)=sqrt(x'*Gamma*x);
end; plot2d(std_x,moyenne_x,style = 1,rect = rectangle);
set_dot(bleu,2); [m,imin]=min(std_x);
plot2d(std_x(imin),moyenne_x(imin),rect = rectangle); set_dot(vert,4);
-
3.
- On autorise l’emprunt de l’actif 1.
N=1000; moyenne_x=0;std_x=0; sigma_e=2; for i=[1:N] do
x=arbitraire(d,sigma_e); moyenne_x(i)=mu*x; std_x(i)=sqrt(x'*Gamma*x);
end; plot2d(std_x,moyenne_x,style = point,rect = rectangle);
f=gcf();Dessin=f.children(1).children(1).children(1); set_dot(rouge,2);
-
4.
- On rajoute un actif sans risque de moyenne nulle.
r0=0; mu=[r0,mu];
Gamma=[zeros(1,d+1);zeros(1,d)',Gamma];
moyenne_actif=mu; std_actif=sqrt(diag(Gamma));
plot2d(std_actif,moyenne_actif,style = 1,rect = rectangle); set_dot(noir,4);
-
5.
- On considère des portefeuilles *avec l’actif sans risque* mais sans emprunt. On les tire au
hasard dans le simplexe.
N=1000; std_x=0;moyenne_x=0; for i=[1:N] do x=simplexe(d+1);
moyenne_x(i)=mu*x; std_x(i)=sqrt(x'*Gamma*x); end;
plot2d(std_x,moyenne_x,style = -1,rect = rectangle); set_dot(bleuclair,2);
-
6.
- Identification du portefeuille de marché P.
N=1000; moyenne_y=0;std_y=0; for i=[1:N] do
y=[0;simplexe(d)];
moyenne_y(i)=mu*y; std_y(i)=sqrt(y'*Gamma*y);
end; r0=mu(1); sigma0=sqrt(Gamma(1,1));
pente=(moyenne_y-r0) ./(std_y-sigma0);
[lambda,imax]=max(pente); x_P=moyenne_y(imax); sigma_P=std_y(imax);
-
7.
- Tracé du portefeuille de marché et de la droite de marché associé.
plot2d(sigma_P,x_P,style = 1,rect = rectangle);
set_dot(red,2);
plot2d([sigma0,sigma_P],[r0,x_P],style = 1,rect = rectangle); set_line(vert,2);
sigma=2.0;
lambda=(x_P-r0)/(sigma_P-sigma0); x=r0+lambda*(sigma-sigma0);
plot2d([sigma0,sigma],[r0,x],style = -1,rect = rectangle); set_line(vert,2);
-
8.
- Avec actif sans risque et emprunt autorisé. On tire au hasard sans imposer le signe de l’actif
sans risque. C’est fait par la primitive arbitraire(d+1,sigma_e) qui faitun choix
(arbitraire) pour la loi de la quantité d’actif sans risque.
N=5000; moyenne_x=0;variance_x=0; for i=[1:N] do
x=arbitraire(d+1,sigma_e); moyenne_x(i)=mu*x;
variance_x(i)=sqrt(x'*Gamma*x); end;
plot2d(variance_x,moyenne_x,style = -2,rect = rectangle); set_dot(mauve,2);
Ce programme est paramétrable pour des valeurs de d et ρ arbitraires, si vous souhaitez
expérimenter par vous même. Toutefois des problèmes d’échantillonage se pose lorsque
d devient grand (au delà de 5, la loi uniforme sur le simplexe “a du mal à visiter les
coins”).
3 Solution des problèmes d’optimisation
-
1.
- Le calcul du portefeuille de marché P, s’exprime sous la forme d’un problème
d’optimisation avec contrainte.
Ce poblème se résout avec des techniques classiques implémentées dans Scicoslab et
qui utilisent vos cours d’optimisation de 1A (passé) et de 2A (futur !).
La fonction [f,xopt]=optim(cost,x0) minimise une fonction, si on lui fournit une
fonction cost qui renvoie la valeur du coût ainsi que de la dérivée du coût en fonction
des paramètres. x0 est la valeur initiale de l’algorithme. optim renvoie la valeur de
l’optimum dans f et le minimiseur dans xopt.
d=30;rho=0.0;
min_esp=0.05;max_esp=0.15; mu=[min_esp:(max_esp-min_esp)/(d-1):max_esp];
min_sigma=0.1;max_sigma=0.3; sigma=[min_sigma:(max_sigma-min_sigma)/(d-1):max_sigma];
correlation=rho*ones(d,d)+(1-rho)*eye(d,d); Gamma=diag(sigma)*correlation*diag(sigma);
function [f,g,ind]=cost(x,ind)
p=prod(size(x))+1;
lambda=[1-sum(x);x]; ps=mu*lambda; var=lambda'*Gamma*lambda;
f=ps^2/var;
k=(2*ps/var)*mu-(2*ps^2/var^2)*lambda'*Gamma;
g=k(2:p)-k(1); f=-f;g=-g;
endfunction x0=ones(d-1,1)/d; [f,xopt]=optim(cost,x0); Xopt=[1-sum(xopt);xopt];
Fopt=sqrt(-f)
ok=and(0 <= Xopt) & and(Xopt <= 1)
sigma=sqrt(diag(Gamma))'; x=(mu ./sigma^2); x=x'/sum(x);
norm(x-Xopt),
-
2.
- La frontière efficiente peut se calculer en résolvant une famille de problème d’optimisation
classique : minimisation de variance à espérance fixée et/ou maximisation d’espérance à
variance fixée.
function lambda=x2lambda(x,R,mu)
p=prod(size(x))+2; alpha0=1-sum(x);
beta0=R-mu(1:p-2)*x; lambda_n_1=(mu(d)*alpha0-beta0)/(mu(d)-mu(d-1));
lambda_n=(beta0-mu(d-1)*alpha0)/(mu(d)-mu(d-1));
lambda=[x;lambda_n_1;lambda_n]; endfunction function [f,g,ind]=cost(x,ind)
p=prod(size(x))+2; lambda=x2lambda(x,R,mu);
k=Gamma*lambda; f=lambda'*k;
for i=[1:p-2] do
g(i)=k(i)+(k(p-1)*(-mu(p)+mu(i))+k(p)*(-mu(i)+mu(p-1)))/(mu(d)-mu(d-1)); end
endfunction d=30;rho=0.0;
min_esp=0.05;max_esp=0.15; mu=[min_esp:(max_esp-min_esp)/(d-1):max_esp];
min_sigma=0.1;max_sigma=0.3; sigma=[min_sigma:(max_sigma-min_sigma)/(d-1):max_sigma];
correlation=rho*ones(d,d)+(1-rho)*eye(d,d); Gamma=diag(sigma)*correlation*diag(sigma);
x0=ones(d-2,1)/d; i=0;abscisse=0;ordonnee=0; for R=[0.05:0.001:0.15] do
[f,xopt]=optim(cost,x0); Xopt=x2lambda(xopt,R,mu); i=i+1;
abscisse(i)=sqrt(f); ordonnee(i)=R; end; plot2d(abscisse,ordonnee);
-
3.
- Toujours en ignorant les contraintes de positivités, on peut obtenir une forme quasi explicite
pour la frontière de Pareto, en utilisant deux multiplicateurs de Lagrange (l’un pour
∑
i=1dλ
i = 1, l’autre pour ∑
i=1dμ
iλi = r).
On obtient après quelques calculs simples, si
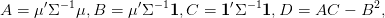
la paramètrisation suivante de la frontière de Pareto : (λ′μ,λ′Σλ) où λ est la fonction de r
suivante :
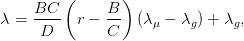
où λg = Σ−11∕C et λ
μ = Σ−1μ∕B. On peut vérifier que seule la partie de cette courbe
correspondant à r ≥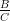 appartient à la frontière de Pareto.
appartient à la frontière de Pareto.
On pourra se convaincre que λg est le point qui minimise la variance des portefeuilles sous la
seule contrainte que ∑
i=1dλ
i = 1 et que λμ est le point qui maximise le ratio de
Sharpe μ′λ∕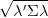 sous la même contrainte (utiliser Cauchy-Schwartz pour s’en
convaincre).
sous la même contrainte (utiliser Cauchy-Schwartz pour s’en
convaincre).
Voir T.J. Brennan and A.W. Lo, 2010, “Impossible frontiers” ou Merton, R., 1972, “An
analytic derivation of the Efficient Portfolio Frontier”.
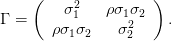
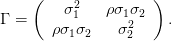
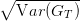 ).
).
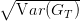 ). Vérifier que, si l’on accepte une
variance grande, on peut constituer des portefeuilles d’espérance aussi grande que souhaitée
(cet effet porte le nom d’effet de levier ou leverage effect). On comprend qu’il ne faille pas en
abuser !
). Vérifier que, si l’on accepte une
variance grande, on peut constituer des portefeuilles d’espérance aussi grande que souhaitée
(cet effet porte le nom d’effet de levier ou leverage effect). On comprend qu’il ne faille pas en
abuser !
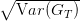 ). Vérifier que lorsque l’on emprunte
l’actif 2 (x2 négatif), l’on fait décroître l’espérance en augmentant la variance (ce qui est loin
d’être optimal !).
). Vérifier que lorsque l’on emprunte
l’actif 2 (x2 négatif), l’on fait décroître l’espérance en augmentant la variance (ce qui est loin
d’être optimal !).
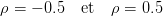
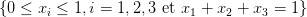 . La
fonction simplexe(d) figurant dans utils.sci pour d = 3 fait ce travail.
. La
fonction simplexe(d) figurant dans utils.sci pour d = 3 fait ce travail.
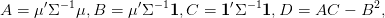
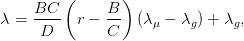
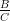 appartient à la frontière de Pareto.
appartient à la frontière de Pareto.
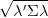 sous la même contrainte (utiliser Cauchy-Schwartz pour s’en
convaincre).
sous la même contrainte (utiliser Cauchy-Schwartz pour s’en
convaincre).