Contents
La séance de TP se fait sous environnement Linux. Pour commencer la séance, ouvrir un shell,
créer un répertoire ’tp_scilab’ (mkdir tp_scilab) puis se placer sous ce répertoire (cd
tp_scilab). Lancer un navigateur, par exemple Mozilla (mozilla &), et aller sur la page web
suivante :
http://cermics.enpc.fr/scilab_new/site/Tp/Probabilites/tp_proba_Q
Lancer ensuite Scilab depuis ce répertoire ’tp_scilab’ (scilab) et ouvrir une fenêtre d’un éditeur,
par exemple emacs (emacs &).
Pour chacune des questions, vous pouvez soit utiliser un “copier-coller”, soit télécharger un
programme Q_i.sce (i = 1..8) qui contient l’essentiel des commandes, avec quelques lignes à
compléter. Pour télécharger le programme Q_i.sce, utiliser par exemple le bouton droit de la
souris et la commande ’Save Link Target as’ puis choisissez le répertoire ’tp_scilab’ et
le nom de fichier Q_i.sce. Il suffit ensuite d’éditer ce programme (par exemple avec
emacs) pour le modifier. Pour l’éxécuter, il suffit de taper sur la ligne de commande
Scilab :
-->exec Q_i.sce;
Pour un rappel sur les opérations élémentaires de Scilab, on renvoie à l’Introduction générale à
Scilab pour les travaux pratiques à l’enpc :
Introduction à Scilab / Manipulations vectorielles
Introduction à Scilab / Graphiques, fonctions Scilab, programmation, saisie de données
On rappelle que pour avoir de l’aide sur une commande Scilab, il suffit de taper sur la ligne de
commande Scilab :
-->help nom_de_la_commande;
1 Test du générateur aléatoire
Nous allons utiliser le générateur aléatoire de Scilab rand. On rappelle que la commande
rand(n,m) renvoie une matrice aléatoire de taille n × m, dont les composantes sont des
réalisations indépendantes de variables aléatoires de loi uniforme sur (0, 1).
Pour le tracé d’histogrammes, nous allons utiliser la commande histplot. On rappelle que la
commande histplot(n,x) trace un histogramme des valeurs contenues dans le vecteur x, avec n
barres de même largeur. On peut également utiliser la commande histplot(r,x), avec r un
tableau donnant les valeurs pour échantillonner x.
Question 1 Générer un vecteur de taille N = 1000 (i.e. une matrice de dimension
(1,N)) dont les composantes sont des réalisations indépendantes de variables aléatoires
de loi uniforme sur (0, 1) avec la fonction rand. Tracer l’histogramme correspondant avec
la fonction histplot. Augmenter N (N = 10 000, 100 000...). Que constatez-vous ?
Pouvez-vous l’expliquer ?
2 Simulation de variables aléatoires de loi exponentielle
Question 2 Choisir un réel λ > 0 et un entier N assez grand (100, 1 000, 10 000...). Écrire
une ligne de code Scilab qui retourne N réalisations indépendantes de loi exponentielle de
paramètre λ. Tracer l’histogramme de ces N réalisations et lui superposer la densité de la
loi exponentielle. Vérifier graphiquement la proximité à la loi originale. (On rappelle qu’en
Scilab, si x est un vecteur, alors log(x) est le vecteur de composantes le logarithme des
composantes de x.)
lambda=0.5;
N=10000;
...
xbasc();
x=linspace(0,12,25); ... // Trace l'histogramme de z échantillonné suivant x
... plot2d(x,y);
3 Simulation de variables aléatoires de loi binomiale
Question 3 Expliquer pourquoi le vecteur y du programme suivant renvoie bien un vecteur
de taille N dont les composantes sont des réalisations d’une variable aléatoire de loi binomiale
de paramètres (n,p). Faire varier p et commenter les résultats.
Cette méthode pour générer des réalisations d’une variable aléatoire de loi binomiale est
préférable à l’utilisation de boucles for qui sont très lentes en Scilab.
On rappelle que la fonction sum(w,’r’) appliquée à une matrice w de taille n×m renvoie
une matrice de taille 1 × m dont chaque composante contient la somme des composantes de
w par colonnes.
n=10;p=0.4;
N=10000;
y=sum(rand(n,N) < p,'r');
xbasc(); [ind,occ]=dsearch(y,0:n,"d");
xbasc();plot2d3(0:n,occ/N,rect = [-1,0,n+1,max(occ/N)*1.1],nax = [0,n+3,1,9]);
plot2d3((0:n)+0.2,binomial(p,n),style = 2);
4 Loi forte des grands nombres
Question 4 Tirer N réalisations indépendantes X1,…, XN d’une loi exponentielle et tracer
le graphique donnant k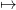
 . Commenter.
. Commenter.
On utilisera la division terme à terme ./ et la fonction cumsum qui évalue des sommes
cumulées, plutôt qu’une boucle. On rappelle par ailleurs que l’on peut générer le vecteur
(1, 2,...,N) sous Scilab par (1:N).
lambda=5;
N=10000;
... xbasc();
... plot(y);
Question 5 Même question avec des Xi i.i.d. suivant une loi de Cauchy de paramètre a.
Exécuter plusieurs fois le programme et commenter.
On rappelle que sous Scilab, la valeur de π est stockée dans %pi.
a=5;
N=1000;
... xbasc();
... plot(y);
5 Théorème de la limite centrale
Question 6 Choisir un entier n assez grand. Tirer n réalisations indépendantes X1,…, Xn
d’une loi uniforme sur [0, 1] et calculer 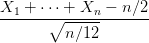 . Choisir un entier N assez
grand. Recommencer N fois et tracer un histogramme de la loi de
. Choisir un entier N assez
grand. Recommencer N fois et tracer un histogramme de la loi de 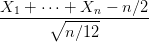 .
Superposer la densité d’une loi normale centrée réduite. Jouer sur les paramètres n et N.
Commenter.
.
Superposer la densité d’une loi normale centrée réduite. Jouer sur les paramètres n et N.
Commenter.
On pourra utiliser la fonction sum(.,’r’)).
n=50; N=1000;
...
... xbasc();
x=linspace(-3,3,25); ... // Trace l'histogramme de z échantillonné suivant x
x=linspace(-3,3,250);
... plot2d(x,y);
6 Simulation de variables aléatoires de loi bêta (2,2) par la méthode du rejet
La variable aléatoire X suit une loi bêta de paramètres (2, 2) si X admet la densité
On propose de simuler cette variable aléatoire par la méthode du rejet en comparant cette loi à la
loi uniforme sur (0, 1). On a évidemment :
 ≤ (3∕2)1[0,1](x ).](tp_proba_Q5x.png) On
sait donc que si on se donne une suite i.i.d. (Y i,Ui) avec Y 1 et U1 indépendants de loi uniforme
sur (0, 1), alors X a même loi que Y N où N = inf
On
sait donc que si on se donne une suite i.i.d. (Y i,Ui) avec Y 1 et U1 indépendants de loi uniforme
sur (0, 1), alors X a même loi que Y N où N = inf 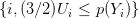 .
.
Question 7 Programmer une fonction qui rend un vecteur de N réalisations indépendantes
suivant la loi bêta de paramètres (2, 2) (on pourra utiliser une boucle while : taper help
while pour avoir une description de la commande). Vérifier que l’on obtient bien la bonne
densité en traçant un histogramme.
function x=rejetbeta(N)
x=zeros(1,N); for i=1:N do
... end;
endfunction N=10000;
z=rejetbeta(N);
x=linspace(0,1,25);
xbasc(); histplot(x,z);
y=6*x .*(1-x) .*(x < 1 & x > 0); plot2d(x,y);
7 Simulation de variables aléatoires de loi normale
Question 8 Choisir un entier N assez grand (100, 1 000, 10 000...). Utiliser la méthode
polaire pour créer un vecteur de taille N dont les composantes sont des réalisations
indépendantes d’une loi normale centrée réduite. Tracer l’histogramme de ces N réalisations
et lui superposer la densité de la loi normale. Vérifier graphiquement la proximité à la loi
originale. On pourra utiliser la multiplication terme à terme .*.
N=1000;
... xbasc();
x=linspace(-3,3,25); ... // Trace l'histogramme de z échantillonné suivant x
x=linspace(-3,3,250);
... plot2d(x,y);
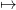
 . Commenter.
. Commenter.
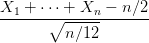
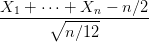
.](tp_proba_Q4x.png)
 ≤ (3∕2)1[0,1](x ).](tp_proba_Q5x.png)
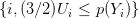 .
.