Question 1 Saisir le fichier de données de température.
Extraire les moyennes annuelles.
Tracer la courbe t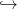 T(t) donnant l’évolution de ces dernières.
T(t) donnant l’évolution de ces dernières.
On trouve sur le site du Climatic Research Unit les moyennes globales de température de 1856 à 2004 (mois par mois et annuelles). Une copie locale où on n’a conservé que les données de température est disponible localement temperature_globe.txt
Question 1 Saisir le fichier de données de température.
Extraire les moyennes annuelles.
Tracer la courbe t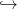 T(t) donnant l’évolution de ces dernières.
T(t) donnant l’évolution de ces dernières.
Question 2 Calculer les coefficients de la droite de régression y = 𝜃1 + 𝜃2t qui est la plus proche de la courbe des températures au sens des moindres carrés.
Question 3 Superposer la courbe des données et la droite de régression.
Question 4 La température T(t) est supposée être une réalisation du modèle T(t) = 𝜃1 + 𝜃2t + 𝜀t, où 𝜀1, 𝜀2... est une suite de variables aléatoires indépendantes de même loi normale 𝒩(0,σ2).
Interpréter en terme de paramètres l’hypothèse (H0) ¡¡ la température est stationnaire ¿¿. Tester cette hypothèse. (On pourra consulter la section 3 a la fin de ce document).
On calcule l’estimateur de σ2 appellé s2
On calcule l’écart type de 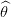 2 à partir de la covariance de
2 à partir de la covariance de 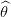 :
:
Alors theta(2)/sigtheta2 suit une loi de Student à (n − 2) degrés de liberté :
Question 5 Examiner graphiquement la courbe des résidus 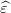 t = T(t) −
t = T(t) −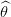 1 −
1 −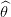 2t.
2t.
Subsiste-t-il une structure dans les résidus ?
Tracer la courbe t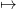 (
(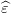 t,T(t)).
t,T(t)).
À l’examen de l’histogramme des résidus, l’hypothèse de normalité vous semble-t-elle raisonnable ?
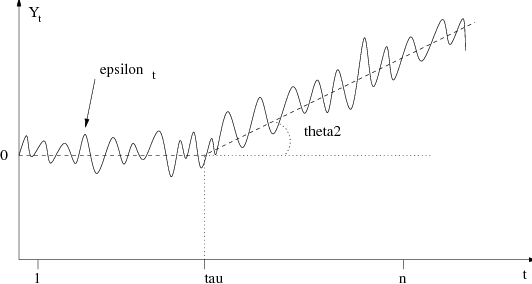
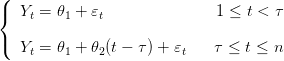 | (1) |
On suppose les 𝜀t indépendants et identiquement distribués (i.i.d.) suivant une loi normale 𝒩(0,σ2).
Le vecteur des paramètres est noté
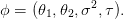 | (2) |
On estime les quatre paramètres par la méthode du maximum de vraisemblance.
La fonction de vraisemblance de la loi normale est définie comme suit :
![( ) [ { τ−1 n }]
---1-- n -1-- ∑ 2 ∑ 2
L (ϕ,Y ) = √ --- exp − 2σ2 (yt − 𝜃1) + (yt − 𝜃1 − 𝜃2(t − τ))
2π σ t=1 t=τ](Stat_clim_Q11x.png) | (3) |
Pour calculer le maximum de vraisemblance, c’est-à-dire les valeurs de 𝜃1, 𝜃2, σ2 et τ qui maximisent log L(ϕ,Y ), on choisit de :
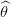 1∗(τ),
1∗(τ), 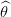 2∗(τ) et
2∗(τ) et 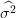 ∗(τ) qui maximisent log L(ϕ,Y ) ;
∗(τ) qui maximisent log L(ϕ,Y ) ;
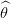 1∗(τ),
1∗(τ),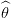 2∗(τ),
2∗(τ),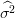 ∗(τ),τ) .
∗(τ),τ) .On effectue donc les opérations dans l’ordre suivant :
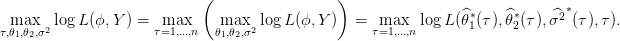
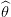 1∗(τ),
1∗(τ), 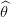 2∗(τ) et
2∗(τ) et 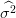 ∗(τ)
∗(τ)
Question 7 Programmer en Scilab le calcul de τ∗ solution de
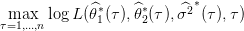
Soient n couples de réels (x1,Y 1),..., (xn,Y n) où seule la seconde composante Y t est aléatoire, supposés suivre le modèle
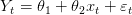 | (6) |
où 𝜀1, 𝜀2... est une suite de variables aléatoires indépendantes de même loi normale 𝒩(0,σ2).
En notations vectorielles, on pose
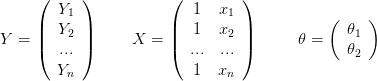
soit
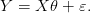
On appelle estimateur de Gauss-Markov (ou estimateur des moindres carrés)
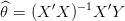 | (7) |
où on a supposé X de rang plein égal à 2. On note
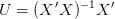 | (8) |
qui satisfait aux relations
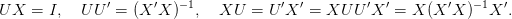 | (9) |
On a
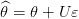 | (10) |
si bien que
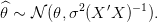 | (11) |
On note le vecteur des résidus
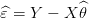 | (12) |
On a
 | (13) |
si bien que
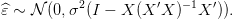 | (14) |
Comme X′ D(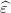 )X = 0, D(
)X = 0, D(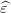 ) est de rang n − 2 car on a supposé X de rang plein égal à 2.
Donc
) est de rang n − 2 car on a supposé X de rang plein égal à 2.
Donc
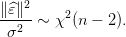 | (15) |
On pose
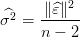 | (16) |
dont on peut vérifier 𝔼(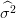 ) = σ2.
) = σ2.
Les vecteurs 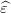 = Y − X
= Y − X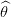 et 𝜃 −
et 𝜃 −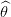 sont indépendants, car le couple
sont indépendants, car le couple
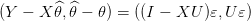 | (17) |
est gaussien décorrélé (propriété de la projection).
Donc le rapport
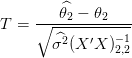 | (18) |
suit une loi de Student à n − 2 degrés de liberté.