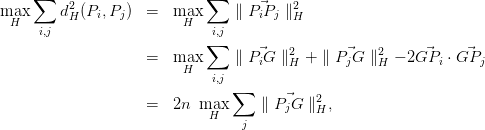
Considérons un nuage ν de n points dans un espace E de dimension p. Lorsque E est de dimension élevée, on ne peut pas visualiser l’espace de points. Un des buts de l’analyse en composantes principales est alors de trouver le meilleur sous-espace H de E, de dimension h égale à 2 ou 3 par exemple, dans lequel on aura la meilleure représentation du nuage. En fait, on va chercher à trouver le sous-espace H de dimension h sur lequel le nuage projeté du nuage ν aura la plus grande ”dispersion”. On cherchera donc à maximiser la somme des carrés des distances entre tous les couples de points projetés.
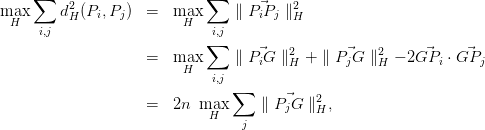
On voit donc que maximiser la somme des carrés des distances entre tous les couples de projetés des points équivaut à maximiser la somme des carrés des distances entre les projetés des points et leur centre de gravité.
Notons (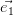 ,…,
,…,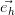 ) une base orthonormée de H.
) une base orthonormée de H.
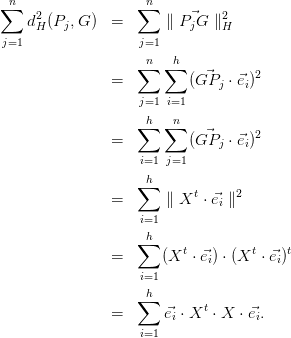
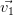 ,…,
,…,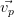 ) la base orthonormée de vecteurs propres associée,
alors λk = max ∥x∥=1,x∈V ect(
) la base orthonormée de vecteurs propres associée,
alors λk = max ∥x∥=1,x∈V ect(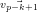 ,…,
,…,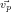 )Q(x). Alors, afin de maximiser l’expression précédente il faut
choisir
)Q(x). Alors, afin de maximiser l’expression précédente il faut
choisir 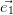 =
= 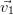 ,…,
,…,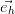 =
= 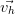 .
.
Dans ce cas, ∑
j=1nd
H2(P
j,G) = ∑
j=1hλ
j est l’inertie du nuage de points ν par rapport au
sous-espace H, et 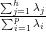 est le pourcentage d’inertie expliqué par le sous-espace H. Ce pourcentage
d’inertie rend compte de la part de dispersion du nuage ν contenue dans le nuage projeté de ν sur
H.
est le pourcentage d’inertie expliqué par le sous-espace H. Ce pourcentage
d’inertie rend compte de la part de dispersion du nuage ν contenue dans le nuage projeté de ν sur
H.
Nous allons étudier dans cette partie la distribution des mesures de poids de différentes parties d’un groupe de 23 bovins1 (cf la table ci-dessous).
Les variables représentent:
| Bovin | X1 | X2 | X3 | X4 | X5 | X6 |
| 1 | 395 | 224 | 35.1 | 79.1 | 6.0 | 14.9 |
| 2 | 410 | 232 | 31.9 | 73.4 | 8.7 | 16.4 |
| 3 | 405 | 233 | 30.7 | 76.5 | 7.0 | 16.5 |
| 4 | 405 | 240 | 30.4 | 75.3 | 8.7 | 16.0 |
| 5 | 390 | 217 | 31.9 | 76.5 | 7.8 | 15.7 |
| 6 | 415 | 243 | 32.1 | 77.4 | 7.1 | 18.5 |
| 7 | 390 | 229 | 32.1 | 78.4 | 4.6 | 17.0 |
| 8 | 405 | 240 | 31.1 | 76.5 | 8.2 | 15.3 |
| 9 | 420 | 234 | 32.4 | 76.0 | 7.2 | 16.8 |
| 10 | 390 | 223 | 33.8 | 77.0 | 6.2 | 16.8 |
| 11 | 415 | 247 | 30.7 | 75.5 | 8.4 | 16.1 |
| 12 | 400 | 234 | 31.7 | 77.6 | 5.7 | 18.7 |
| 13 | 400 | 224 | 28.2 | 73.5 | 11.0 | 15.5 |
| 14 | 395 | 229 | 29.4 | 74.5 | 9.3 | 16.1 |
| 15 | 395 | 219 | 29.7 | 72.8 | 8.7 | 18.5 |
| 16 | 395 | 224 | 28.5 | 73.7 | 8.7 | 17.3 |
| 17 | 400 | 223 | 28.5 | 73.1 | 9.1 | 17.7 |
| 18 | 400 | 224 | 27.8 | 73.2 | 12.2 | 14.6 |
| 19 | 400 | 221 | 26.5 | 72.3 | 13.2 | 14.5 |
| 20 | 410 | 233 | 25.9 | 72.3 | 11.1 | 16.6 |
| 21 | 402 | 234 | 27.1 | 72.1 | 10.4 | 17.5 |
| 22 | 400 | 223 | 26.8 | 70.3 | 13.5 | 16.2 |
| 23 | 400 | 213 | 25.8 | 70.4 | 12.1 | 17.5 |
On dipose d’une matrice poids de taille (23, 6) correspondant aux poids des 23 bovins selon les 6 critères. (fichier poids.txt). On charge les données dans Scilab, après avoir sauvegardé localement le fichier par exemple sous le nom poids.txt, à l’aide de la commande
poids=fscanfMat("poids.txt")
L’analyse des données nous conduit tout d’abord à calculer les paramètres descriptifs élémentaires presentés dans le tableau ci dessous.
| Moyenne | Écart-type | Min | Max | |
| X1 | 401.6 | 8.2 | 390.0 | 420.0 |
| X2 | 228.8 | 8.7 | 213.0 | 247.0 |
| X3 | 29.9 | 2.6 | 25.8 | 35.1 |
| X4 | 74.7 | 2.5 | 70.3 | 79.1 |
| X5 | 8.9 | 2.4 | 4.6 | 13.5 |
| X6 | 16.6 | 1.2 | 14.5 | 18.7 |
L’écart-type d’une suite de poids P1,…,Pn est estimé par: 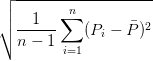 , où
=
, où
= 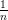 ∑
i=1nP
i.
∑
i=1nP
i.
La matrice des corrélations nous donne une première idée des associations existant entre les différentes variables.
| X1 | X2 | X3 | X4 | X5 | X6 | |
| X1 | 1.0000 | 0.6914 | -0.0329 | -0.0585 | 0.0820 | 0.0820 |
| X2 | 0.6914 | 1.0000 | 0.2837 | 0.3903 | -0.3363 | 0.0917 |
| X3 | -0.0329 | 0.2837 | 1.0000 | 0.8948 | -0.8773 | 0.0348 |
| X4 | -0.0585 | 0.3903 | 0.8948 | 1.0000 | -0.9016 | 0.0032 |
| X5 | 0.0820 | -0.3363 | -0.8773 | -0.9016 | 1.0000 | -0.3368 |
| X6 | 0.0820 | 0.0917 | 0.0348 | 0.0032 | -0.3368 | 1.0000 |
La matrice de corrélations est obtenue en exécutant la fonction correlation. MatCor=correlation(poids).
Cette fonction fait appel à la fonction covariance.
Calculons les valeurs propres de la matrice des corrélations et intéressons nous aux pourcentages d’inertie.
| Axe | Valeur propre | Inertie | Inertie cumulée |
| 1 | 2.9914 | 49.90% | 49.90% |
| 2 | 1.6125 | 26.90% | 76.80% |
| 3 | 1.0387 | 17.30% | 94.10% |
| 4 | 0.2487 | 4.10% | 98.20% |
| 5 | 0.0758 | 1.30% | 99.50% |
| 6 | 0.0329 | 0.50% | 100.00% |
Les valeurs propres sont calculées sur la matrice de corrélation avec la fonction valprop.
L’inertie expliquée par la i-ème composante principale, qui est associée à la i-ème plus grande
valeur propre, est calculée avec la formule: 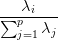 .
.
Question 1 Analyser le résultat obtenu.
Les vecteurs propres sont calculés sur la matrice de corrélation avec la fonction vectprop qui renvoie les vecteurs propres rangés dans l’ordre décroissant des valeurs propres associées.
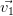 | 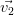 | 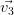 | 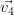 | 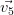 | 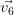 |
|
| X1 | 0.063 | 0.743 | 0.060 | 0.597 | 0.283 | -0.063 |
| X2 | 0.304 | 0.609 | 0.117 | -0.643 | -0.331 | 0.019 |
| X3 | 0.534 | -0.164 | 0.137 | 0.461 | -0.646 | 0.200 |
| X4 | 0.548 | -0.138 | 0.176 | -0.130 | 0.595 | 0.528 |
| X5 | -0.552 | 0.147 | 0.172 | 0.032 | -0.193 | 0.778 |
| X6 | 0.120 | 0.100 | -0.950 | 0.007 | -0.040 | 0.266 |
Nous obtenons, à partir de la matrice des données, les coordonnées des projetés des individus dans la base orthonormée des vecteurs propres de la matrice des corrélations avec la fonction acpindiv.
Cette fonction fait appel à la fonction reduire qui permet de centrer et de normer une matrice de données de telle sorte que la moyenne de chaque variable soit nulle et que son écart-type soit égal à 1.
Les coordonnées, calculées à partir de la matrice des données, des variables dans la base orthonormée des vecteurs propres sont obtenues avec la fonction acpvar.
Cela nous permet de représenter le nuage projeté du nuage initial de poids et le cercle des corrélations dans le plan formé par deux composantes principales quelconques.
Question 2 Que pouvez-vous dire sur le cercle des corrélations du plan factoriel 1-2?
Pour représenter les coordonnées de m points de ℝp sur les axes i-j, on utilise la fonction nuage, où les lignes de la matrice A sont les coordonnées des m points de ℝp.
Pour représenter le cercle des corrélations sur les axes i-j, on utilise la fonction cercle(A,i,j) ( cercle), où A est la matrice des coordonnées des variables dans la base orthonormée des vecteurs propres.
Question 3 Que pouvez-vous dire sur le cercle des corrélations du plan factoriel 2-3?
La qualité est représentée par le cosinus de l’angle entre le vecteur et son projeté sur le plan factoriel considéré.
On utilise la fonction qualiteindiv(poids,i,j) (qualiteindiv.sce) pour représenter la qualité des individus sur les plans factoriels i-j.
Question 4 Quelle est votre analyse pour la qualité de la représentation sur les plans 1-2 et 2-3?
Les données proviennent de deux races Charolais ou Zébu.
Le programme barycentres(acpindiv(poids),race,i,j) ( barycentres ) permet de visualiser la variable nominale supplémentaire race dans le plan factoriel i-j.
Question 5 Analyser le rôle de la variable nominale.