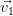 ,…,
,…,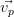 ) la base
orthonormée de vecteurs propres associée.
) la base
orthonormée de vecteurs propres associée.
Considérons un nuage ν de n points dans un espace E de dimension p. Lorsque E est de dimension élevée, on ne peut pas visualiser l’espace de points. Un des buts de l’analyse en composantes principales est alors de trouver le meilleur sous-espace H de E, de dimension h égale à 2 ou 3 par exemple, dans lequel on aura la meilleure représentation du nuage. En fait, l’analyse en composantes principales cherche à trouver le sous-espace H de dimension h sur lequel le nuage projeté du nuage ν aura la plus grande ”dispersion”.
Soit X la matrice où Xi,j, 1 ≤ i ≤ n, 1 ≤ j ≤ p est la valeur de la j-ème variable pour le i-ème point.
Notons (λ1 ≥… ≥ λp) le spectre de la matrice symétrique réelle Xt ⋅ X et (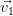 ,…,
,…,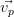 ) la base
orthonormée de vecteurs propres associée.
) la base
orthonormée de vecteurs propres associée.
Pour tout 1 ≤ h ≤ p, ∑
j=1hλ
j est l’inertie du nuage de points ν par rapport au sous-espace H
engendré par (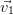 ,…,
,…,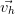 ) , et
) , et 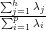 est le pourcentage d’inertie expliqué par le sous-espace H. Ce
pourcentage d’inertie rend compte de la part de dispersion du nuage ν contenue dans le nuage
projeté de ν sur H.
est le pourcentage d’inertie expliqué par le sous-espace H. Ce
pourcentage d’inertie rend compte de la part de dispersion du nuage ν contenue dans le nuage
projeté de ν sur H.
Nous allons étudier dans cette partie la distribution des mesures de poids de différentes parties d’un groupe de 23 bovins1 (cf la table ci-dessous).
Les variables représentent:
| Bovin | X1 | X2 | X3 | X4 | X5 | X6 |
| 1 | 395 | 224 | 35.1 | 79.1 | 6.0 | 14.9 |
| 2 | 410 | 232 | 31.9 | 73.4 | 8.7 | 16.4 |
| 3 | 405 | 233 | 30.7 | 76.5 | 7.0 | 16.5 |
| 4 | 405 | 240 | 30.4 | 75.3 | 8.7 | 16.0 |
| 5 | 390 | 217 | 31.9 | 76.5 | 7.8 | 15.7 |
| 6 | 415 | 243 | 32.1 | 77.4 | 7.1 | 18.5 |
| 7 | 390 | 229 | 32.1 | 78.4 | 4.6 | 17.0 |
| 8 | 405 | 240 | 31.1 | 76.5 | 8.2 | 15.3 |
| 9 | 420 | 234 | 32.4 | 76.0 | 7.2 | 16.8 |
| 10 | 390 | 223 | 33.8 | 77.0 | 6.2 | 16.8 |
| 11 | 415 | 247 | 30.7 | 75.5 | 8.4 | 16.1 |
| 12 | 400 | 234 | 31.7 | 77.6 | 5.7 | 18.7 |
| 13 | 400 | 224 | 28.2 | 73.5 | 11.0 | 15.5 |
| 14 | 395 | 229 | 29.4 | 74.5 | 9.3 | 16.1 |
| 15 | 395 | 219 | 29.7 | 72.8 | 8.7 | 18.5 |
| 16 | 395 | 224 | 28.5 | 73.7 | 8.7 | 17.3 |
| 17 | 400 | 223 | 28.5 | 73.1 | 9.1 | 17.7 |
| 18 | 400 | 224 | 27.8 | 73.2 | 12.2 | 14.6 |
| 19 | 400 | 221 | 26.5 | 72.3 | 13.2 | 14.5 |
| 20 | 410 | 233 | 25.9 | 72.3 | 11.1 | 16.6 |
| 21 | 402 | 234 | 27.1 | 72.1 | 10.4 | 17.5 |
| 22 | 400 | 223 | 26.8 | 70.3 | 13.5 | 16.2 |
| 23 | 400 | 213 | 25.8 | 70.4 | 12.1 | 17.5 |
On dispose d’une matrice poids de taille (23, 6) correspondant aux poids des 23 bovins selon les 6 critères (fichier poids.txt). On charge les données dans Scilab, après avoir sauvegardé localement le fichier par exemple sous le nom poids.txt, à l’aide de la commande
L’analyse des données nous conduit tout d’abord à calculer les paramètres descriptifs élémentaires presentés dans le tableau ci dessous.
| Moyenne | Écart-type | Min | Max | |
| X1 | 401.6 | 8.2 | 390.0 | 420.0 |
| X2 | 228.8 | 8.7 | 213.0 | 247.0 |
| X3 | 29.9 | 2.6 | 25.8 | 35.1 |
| X4 | 74.7 | 2.5 | 70.3 | 79.1 |
| X5 | 8.9 | 2.4 | 4.6 | 13.5 |
| X6 | 16.6 | 1.2 | 14.5 | 18.7 |
L’écart-type d’une suite de poids P1,…,Pn est estimé par:
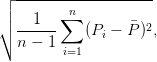
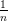 ∑
i=1nP
i.
∑
i=1nP
i.
La matrice des corrélations nous donne une première idée des associations existant entre les différentes variables.
| X1 | X2 | X3 | X4 | X5 | X6 | |
| X1 | 1.0000 | 0.6914 | -0.0329 | -0.0585 | 0.0820 | 0.0820 |
| X2 | 0.6914 | 1.0000 | 0.2837 | 0.3903 | -0.3363 | 0.0917 |
| X3 | -0.0329 | 0.2837 | 1.0000 | 0.8948 | -0.8773 | 0.0348 |
| X4 | -0.0585 | 0.3903 | 0.8948 | 1.0000 | -0.9016 | 0.0032 |
| X5 | 0.0820 | -0.3363 | -0.8773 | -0.9016 | 1.0000 | -0.3368 |
| X6 | 0.0820 | 0.0917 | 0.0348 | 0.0032 | -0.3368 | 1.0000 |
La matrice de corrélations est obtenue en exécutant la fonction MatCor=correlation(poids) ( correlation).
Cette fonction fait appel à la fonction covariance.
Calculons les valeurs propres de la matrice des corrélations et intéressons nous aux pourcentages d’inertie.
| Axe | Valeur propre | Inertie | Inertie cumulée |
| 1 | 2.9914 | 49.90% | 49.90% |
| 2 | 1.6125 | 26.90% | 76.80% |
| 3 | 1.0387 | 17.30% | 94.10% |
| 4 | 0.2487 | 4.10% | 98.20% |
| 5 | 0.0758 | 1.30% | 99.50% |
| 6 | 0.0329 | 0.50% | 100.00% |
Les valeurs propres sont calculées sur la matrice de corrélation avec la fonction valprop.
L’inertie expliquée par la i-ème composante principale, qui est associée à la i-ème plus grande
valeur propre, est calculée avec la formule: 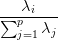 .
.
Question 1 Analyser le résultat obtenu.
Les vecteurs propres sont calculés sur la matrice de corrélation avec la fonction [valpr,vectpr]=vectprop(MatCor) (vectprop.sce) qui renvoie les valeurs propres rangées dans l’ordre décroissant et les vecteurs propres associées.
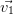 | 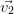 | 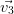 | 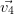 | 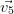 | 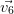 |
|
| X1 | 0.063 | 0.743 | 0.060 | 0.597 | 0.283 | -0.063 |
| X2 | 0.304 | 0.609 | 0.117 | -0.643 | -0.331 | 0.019 |
| X3 | 0.534 | -0.164 | 0.137 | 0.461 | -0.646 | 0.200 |
| X4 | 0.548 | -0.138 | 0.176 | -0.130 | 0.595 | 0.528 |
| X5 | -0.552 | 0.147 | 0.172 | 0.032 | -0.193 | 0.778 |
| X6 | 0.120 | 0.100 | -0.950 | 0.007 | -0.040 | 0.266 |
Les coordonnées, calculées à partir de la matrice des données, des variables dans le système orthonormée des composantes principales normalisées sont obtenues avec la fonction V=acpvar(poids) acpvar.sce.
Cette fonction fait appel à la fonction reduire qui permet de centrer et de normer une matrice de données de telle sorte que la moyenne de chaque variable soit nulle et que son écart-type soit égal à 1.
Cela nous permet de représenter le cercle des corrélations dans le plan formé par les deux composantes principales. Pour représenter le cercle des corrélations sur les axes i-j, on utilise la fonction cercle(V,i,j) (cercle).
Question 2 Tracer le cercle des corrélations du plan factoriel 1-2. Commenter.
Les données proviennent de deux races Charolais ou Zébu.
Nous obtenons, à partir de la matrice des données, les coordonnées des individus dans la base orthonormée des vecteurs propres de la matrice des corrélations avec la fonction acpindiv (acpindiv(poids)).
Le programme representation(acpindiv(poids),race,i,j) (representation) permet de visualiser la variable nominale supplémentaire race dans le plan factoriel i-j.
Question 3 En déduire une méthode de classement d’un bovin en zébu ou charolais basée sur l’observations des variables caractérisant le bovin.
La reconnaissance de caractères manuscrits par un système automatisé est un problème aux multiples applications: reconnaissance des codes postales, création de petit système mobile de saisie de texte (par exemple, pour les ordinateurs de poche), numérisation de documents manuscrits, ...
Les méthodes les plus performantes pour reconnaître un caractère manuscrit sont basées sur des méthodes d’apprentissage statistique: leur principe commun est de fonder leur prédiction sur la comparaison de l’image du caractère manuscrit à classer à d’autres images de caractères manuscrits pour lesquels la nature du caractère est connue. Typiquement, si une image arrive et qu’elle est très similaire à l’image de nombreux ’1’ de notre base d’apprentissage, l’algorithme classera l’image dans la catégorie ’1’.
Les données considérées ici proviennent de la base MNIST (http://yann.lecun.com/exdb/mnist/) sur laquelle des milliers de chercheurs ont travaillé. Elle est constituée de 70 000 chiffres manuscrits au format 28 pixels par 28 pixels où chaque pixel est représenté par un niveau de gris allant de 1 à 256 (i.e. un chiffre manuscrit est donc un vecteur de {1,…, 256}28×28).


Dans ce TP, pour limiter le temps de calcul et la mémoire nécessaire, nous ne considérons que 800 chiffres manuscrits (que des ’3’ et des ’5’): 400 chiffres manuscrits seront utilisés pour apprendre, i.e. calibrer l’algorithme. Ces 400 chiffres manuscrits et la classe (’3’ ou ’5’) qui leur est associée constituent l’ensemble d’apprentissage. Les 400 autres chiffres manuscrits seront uniquement utilisés pour évaluer la qualité des algorithmes. Ces 400 caractères manuscrits constituent donc l’ensemble de test.
On dispose d’une matrice de taille (800, 1 + (28 × 28)) correspondant aux poids des 800 caractères manuscrits où
On charge les données dans Scilab, après avoir sauvegardé localement les fichiers chiffres3.txt et chiffres5.txt contenant les ’3’ et les ’5’, à l’aide des commandes:
En cas de message d’erreur concernant la taille de la pile, on peut augmenter la taille maximale de cette dernière à l’aide de la commande stacksize(new_size).
On considère l’algorithme du plus proche voisin pour la distance euclidienne entre les vecteurs de ℝ28×28 que sont les images de caractères manuscrits.
La fonction classe(EnsTest,EnsApprentissage) (nearest.sce) permet de classer les données de test en appliquant l’algorithme du plus proche voisin basé sur l’ensemble d’apprentissage EnsApprentissage. Elle renvoie le taux des données de l’ensemble EnsTest ayant été mal classées par la méthode. Les ensembles d’apprentissage et de test sont respectivement composés des 200 premiers chiffres et des 200 derniers.
Question 4 Quel est le pourcentage de caractères manuscrits de l’ensemble de test mal classés par l’algorithme du plus proche voisin. Critiquer la méthode utilisée.
La matrice des covariances est obtenue en exécutant la fonction covariance(chiffres_sans_label). Les valeurs propres sont calculées sur la matrice de covariance avec la fonction
Question 5 Analyser l’éboulis des valeurs propres. Combien de composantes doivent être conservées pour avoir plus de 95% de l’inertie. (On pourra utiliser le code ’sum(A(1:k))’ qui permet de faire la somme des k premiers éléments d’un vecteur A.)
La fonction [M_proj] = projection(M, vectpr, k) (projection.sce) renvoie la projection de la matrice M sur les k premiers vecteurs propres.
Question 6 Afficher les images associées aux directions principales choisies à la question précédente. Pour quelles valeurs de k, les composantes principales contiennent-elles suffisamment d’informations pour que le chiffre soit toujours aussi reconnaissable par l’oeil humain?
Pour afficher les images associées aux directions principales choisies à la question précédente, on pourra utiliser la fonction show_mat.sce et le code suivant
Question 7 Appliquer l’algorithme du plus proche voisin pour les différentes valeurs de k (c’est-à-dire, lorsque la distance euclidienne utilisée est celle sur les vecteurs composés par les k composantes principales). Au vu des résultats sur l’ensemble test, comment choisir k pour avoir les meilleurs résultats? Quelle est l’inertie contenue par ces composantes? Commenter. En pratique, nous ne connaissons pas l’ensemble test. Comment peut-on choisir k en pratique?