Avec les indication du TP quand à l’écriture des fonctions Ghil_1 et Ghil_2 et à l’usage de fcontour2d pour le tracé des isoclines, on obtient, pour μ = 1.8 le graphe suivant :
On observe clairement trois points d’équilibre.
On retrouve les trois points d’équilibre : le champ de vecteurs tourne autour, ou s’en écarte. On peut déjà remarquer la nature de ces points : le point central a plutôt l’air d’être un attracteur, tandis que les deux autres ressemblent à des points selles. Cette impression pourra être confirmée par l’examen de quelques trajectoires.
Lorsque l’on choisit une condition initiale en bas au milieu du portrait, la trajectoire solution est attirée en spirale vers le point d’équilibre central, ce qui confirme sa nature attractrice.
Les deux autres points d’équilibre semblent attirer les trajectoires venant d’une direction et repousser celles venant de la direction perpendiculaire. Il semble donc bien qu’il s’agisse de points-selle.
En faisant varier le paramètre de bifurcation μ, on observe une différence de comportement dans les portraits de phase, confirmée par l’étude des variations de température correspondantes.
Dans les pages suivantes, nous avons retracé les portraits de phase et les variations de température dans chaque cas.
Sur la figure 5, les trajectoires partant du bas du portrait contournent le point central et partent vers la gauche du portrait, tandis que celles partant d’une condition initiale proche du point central s’en éloignent.
Le point d’équilibre central est clairement répulsif.
Nous avons tracé les courbes de température grâce aux fonctions ode et plot. Afin de toujours tracer des vecteurs de même taille, même en cas de divergence, nous avons entré les lignes suivantes :
Si on choisit μ = 1.5, et T = 280K, L = 8.105m comme conditions initiales, on obtient le graphe 5.
L’amplitude des oscillations augmente clairement avec le temps jusqu’à diverger. On retrouve ce que l’on pouvait voir sur le portrait de phase précédent : le point est répulsif, la trajectoire s’en éloignent en tourant autour pour finalement “sortir” du portrait vers la gauche, soit vers les températures plus basses.
Cette fois-ci, sur la figure 6, les trajectoires ne se comportent pas tout à fait de la même façon.
En effet, les trajectoires partant du bas du portrait de phase sont toujours attirées vers le point d’équilibre, mais elles l’entourent sans plus l’approcher à partir d’un moment. Au contraire, les trajectoires partant de la zone proche du point d’équilibre s’en écartent pour rejoindre les trajectoires précédentes.
Nous constatons ici l’apparition d’un attracteur d’un autre type : il s’agit d’un cycle limite.
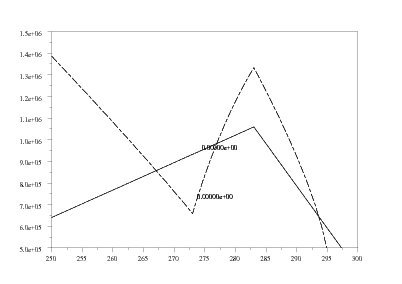
Sur la figure 7, la température se retrouve rapidement en régime oscillatoire d’amplitude constante égale à 14 K environ. Cela confirme l’existence d’un cycle limite. La période des oscillations est de 8 unités de temps environ.
Le portrait de phase8 obtenu avec cette valeur de μ n’est pas aisé à qualifier : il semble qu’il y ait plusieurs cycles limites ; on ne peut trancher véritablement quant à la nature des attracteurs (soit un point, soit un cycle limite). La convergence vers l’attracteur est en tout cas très lente.
Une courbe de la température sur une grande échelle de temps pourrait aider à déterminer la nature de l’attracteur.
D’après la courbe 9, la nature de l’attracteur est explicite : nous sommes en présence d’un point attracteur. Il n’y a plus de cycle limite.
Sur la figure 10, la nature de l’attracteur est ici bien plus facilement dicernable : il s’agit d’un point. On peut remarquer que, lorsque μ augmente, la convergence des trajectoires vers l’attracteur est plus rapide.
La convergence vers le point attracteur est nette sur la courbe 11 : la température se stabilise vers 277 K (soit une différence de 4 K avec la condition initiale).
Afin d’estimer la période des oscillations, nous allons “zoomer” sur le début du graphe.
On observe une période des oscillations d’environ 5 unités de temps.