Equilibrio y Estabilidad en el Manejo de un Recurso Renovable

Michel De Lara and Luc Doyen
Traducido por Beatriz Salguero y Paula Andrea González (UAO, Cali, Colombia)
(last modification date: March 7, 2018)
Version pdf de ce document
Version sans bandeaux

1 El modelo Beverton-Holt
2 El modelo logístico
3 El modelo de Ricker

Contents

1 El modelo Beverton-Holt
2 El modelo logístico
3 El modelo de Ricker

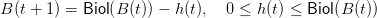
Sea t el tiempo medido en unidades discretas (tales como años). Sea B(t) la biomasa de una población en el tiempo t (en el intervalo [t,t + 1)). Se considera el modelo de Schaefer

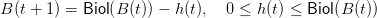B (t + 1) = Biol(B(t)) − h(t), 0 ≤ h(t) ≤ Biol(B (t))
(1)

donde Biol es la dinámica de la población y h(t) es la cosecha o recolección de la especie considerada. Note que, en el intervalo de tiempo [t,t + 1), primero se dá el crecimiento de la población existente y luego la cosecha1 .

El rendimiento sostenible he = Sust(Be) resuelve Be = Biol(Be) − he, del cual se obtiene:

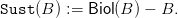Sust (B ) := Biol(B ) − B.
(2)

La capacidad de carga es el nivel K > 0 de biomasa positiva tal que Biol(K) = K, es decir Sust(K) = 0.

El máximo rendimiento sostenible hmse y el correspondiente máximo equilibrio sostenible Bmse están dados por

hmse := sup[Biol(B ) − B] y Bmse := argmax [Biol(B ) − B ]. B≥0 B≥0
(3)

De [1, p. 258] y a partir de simulaciones numéricas, se considera como ejemplo el Atún Aleta Amarilla del Pacífico con los valores de los parámetros dados en la Tabla 1.

Atún Aleta Amarilla del Pacífico
Crecimiento intrínseco anual R = 2.25
Capacidad de carga K = 250 000 toneladas métricas
capturabilidad q = 0.0000385 por DEP
Precio p = $ 600 por tonelada métrica
Costo c = $ 2500 por DEP

Table 1: Datos Atún Aleta Amarilla del Pacífico para un modelo logístico en tiempo discreto (adaptado de [1, p. 258]). DEP: día estándar de pesca.

1 El modelo Beverton-Holt

El modelo Beverton-Holt está dado por la ecuación en tiempo discreto

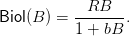--RB--- Biol(B ) = 1 + bB .
(4)

donde

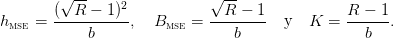-- -- (√ R − 1)2 √ R − 1 R − 1 hmse = ----------, Bmse = -------- y K = ------. b b b
(5)

Pregunta 1 Usando los datos de la Tabla 1 calcule b en (4), dada la máxima biomasa sostenible Bmse y el rendimiento máximo sostenible hmse como en (5).

   R_tuna = 2.25 ;
    K_tuna = 250000 ; // toneladas metricas
  
    // DINAMICA  BEVERTON-HOLT
    R_BH = R_tuna ;
    b_BH = (R_BH-1) / K_tuna ;
  
    function [y]=Beverton(B)
    y=(R_BH*B)./(1 + b_BH*B) ;
    y=maxi(0,y) ;
    endfunction;
  
    // RENDIMIENTO SOSTENIBLE
    function [SY]=sust_yield(dynamic,B), SY=dynamic(B)-B, endfunction;
  
  
    // EQUILIBRIO MAXIM0 SOSTENIBLE
    B_MSE = (sqrt(R_BH) - 1)/b_BH ;
    // rendimiento maximo sostenible
    h_MSE = sust_yield(Beverton,B_MSE) ;
    // rendimiento maximo sostenible

Pregunta 2 Seleccione un nivel de biomasa Be entre la máxima biomasa sostenible Bmse y la capacidad de carga K. Calcule el rendimiento sostenible correspondiente he.

Dibuje la trayectoria estacionaria correspondiente al modelo de Schaefer (1) con la dinámica de Beverton-Holt (4) y h(t) = he. Dadas dos condiciones iniciales diferentes en la vecindad del equilibrio de la biomasa Be, dibuje las trayectorias correspondientes. Determine si la gráfica confirma o no que el equilibirio de la biomasa Be es un atractor.

Recuerde que para un equilibrio, los conceptos de ser estable o ser atractor no están relacionados.

Pregunta 3 La gráfica confirma o no el hecho de que el equilibrio de la biomasa Be es estable? Justifique claramente su respuesta. Qué se puede decir acerca de la estabilidad asintótica del equilibrio de la biomasa Be?

    // EQUILIBRIO SOSTENIBLE
  
    alpha=rand();
    Be= alpha*B_MSE + (1-alpha)*K_tuna ;
    // seleccione uno de los posibles equilibrios
    he=sust_yield(Beverton,Be) ;
    //rendimiento sostenible correspondiente
  
  
    function [y]=sequential(y0,time,f)
    [one,two]=size(Binit) ;
    y=zeros(one,prod(size(time))) ; // time es un vector t0, t0+1,...,T
    // vector que contiene las trayectorias y(1),...,y(T-t0+1)
    // para diferentes condiciones iniciales
    for k=1:one
    y(k,1)=y0(k);
    // inicializacion
    for s=time(1:($-1)) -time(1)+1
    //ejecute desde 1 to T-t0+1
    y(k,s+1)=f(s,y(k,s));
    end ;
    end ;
    endfunction
  
  
    // TRAYECTORIAS DE ESTADO  BAJO LA DINAMICA
  
    function [y]=Beverton_e(t,B)
    y=Beverton(B) - he ;
    y=maxi(0,y) ;
    endfunction
    // dinamica Beverton-Holt  con recoleccion en el equilibrio (Be,he)
  
    T=20;
    years =1:(T+1);
  
    xset("window",31); xbasc(31);
    Binit=Be;
    Bt=sequential(Binit,years,Beverton_e);
    plot2d2(years',Bt',1);
    //
    Binit=0.9*Be ;
    Bt=sequential(Binit,years,Beverton_e);
    plot2d2(years',Bt',2);
    //
    Binit=1.1*Be;
    // Parece que hay un error con la versión anterior de 'sequential'
    Bt=sequential(Binit,years,Beverton_e);
    plot2d2(years',Bt',3);
    //
    xtitle('Trayectorias con la dinámica Beverton-Holt (R=' +string(R_tuna)...
    +' and K=' +string(K_tuna) +')', 'años (t)','B(t)')
    legends(['biomasa en equilibrio'],[1],'ur')

PIC


Figure 1: Trayectorias de biomasa del Atún Aleta Amarilla del Pacífico con la dinámica Beverton-Holt

Pregunta 4 Encuentre un estado de equilibrio Be que no sea un atractor. Muestre que Be no es atractor con algunas trayectorias. Qué se puede decir acerca de la estabilidad asintótica de la biomasa en equilibrio Be?

Con precio p, y coeficiente de captura q y costos unitarios de recolección c, el equilibrio de propiedad privada (ppe) es la solución de equilibrio (Bppe,hppe) = (Bppe,Sust(Bppe)) la cual maximiza la renta como sigue:

ch max [ph − ---]. B≥0,h=Sust(B ) qB
(6)

El equilibrio de propiedad común Bcpe hace que la renta sea nula y está dada por

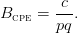c Bcpe = --. pq
(7)

Pregunta 5 Analice la estabilidad alrededor de los siguientes equilibrios:

Compare sus observaciones con los resultados teóricos.

  // Parametros economicos
    c_tuna=2500; // Costo unitario de esfuerzo
    p_tuna=600; // Precio en el mercado
    q_tuna=0.0000385; // capturabilidad
  
    c=c_tuna;
    p=p_tuna;
    q=q_tuna;
  
    B_PPE= ( sqrt( R_BH * (1 + (b_BH*c/(p*q)) ) ) - 1 ) / b_BH;
   // equilibrio de propiedad privada
  
  
    B_CPE=c/(p*q) ;
    // equilibrio de propiedad comun
  

2 El modelo logístico

El modelo logístico es caracterizado por la ecuación en tiempo discreto

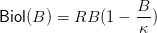B Biol(B ) = RB (1 − --) κ
(9)

donde R ≥ 1 y r = R − 1 ≥ 0 es la tasa per-capita de crecimiento (para pequeñas poblaciones), y κ está relacionado con la capacidad de carga K (La cual resuelve Biol(K) = K) como:

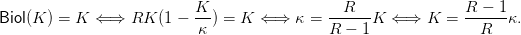Biol(K ) = K ⇐ ⇒ RK (1 − K-) = K ⇐⇒ κ = --R---K ⇐ ⇒ K = R-−-1κ. κ R − 1 R
(10)

Se tiene

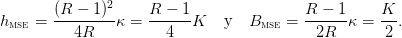(R--−-1)2 R--−-1 R-−-1- K-- hmse = 4R κ = 4 K y Bmse = 2R κ = 2 .
(11)

Pregunta 6 Adapte el anterior código Scilab al modelo logístico, y compare los resultados.

3 El modelo de Ricker

El modelo de Ricker está caracterizado por la ecuación en tiempo discreto

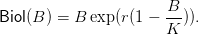B-- Biol(B ) = B exp (r(1 − K )).
(12)

Pregunta 7

Adapte el anterior código Scilab al modelo de Ricker , y compare los resultados. Intente procedimientos numéricos: escribiendo help fsolve para obtener información acerca del solver Scilab.

References

[1]   M. Kot. Elements of Mathematical Ecology. Cambridge University Press, Cambridge, 2001.