Attracteurs de systèmes dynamiques
Les questions

Stéphane Binois
(last modification date: October 10, 2017)
Version pdf de ce document
Version sans bandeaux

1 Un système dynamique à cycle limite
2 L’attracteur de Lorenz
3 Évolution d’un attracteur en fonction d’un des paramètres du système

Contents

1 Un système dynamique à cycle limite
 1.1 Quel est le système étudié ?
 1.2 Visualisation de cycles limite sous Scilab
2 L’attracteur de Lorenz
 2.1 Les équations du système de Lorenz
 2.2 Visualisation de l’attracteur de Lorenz sous Scilab
3 Évolution d’un attracteur en fonction d’un des paramètres du système
 3.1 De quoi s’agit-il ?
 3.2 Quel est le modèle utilisé ?
 3.3 Simulation sous Scilab

1 Un système dynamique à cycle limite

1.1 Quel est le système étudié ?

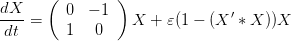
Il s’agit d’un système dynamique auquel on adjoint une perturbation quadratique dont on peut régler l’amplitude à l’aide du paramètre epsilon.

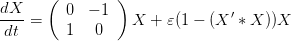dX ( 0 − 1 ) ----= X + 𝜀(1 − (X ′ ∗ X ))X dt 1 0
(1)

L’objet du TD va être d’étudier différents comportements de ce système selon les valeurs prises par le paramètre epsilon.

1.2 Visualisation de cycles limite sous Scilab

On définit une variable epsilon=0,5.

Visualiser le champ de vecteurs ainsi que quelques trajectoires (en lançant la commande portrait(cycllim)). On pourra prendre [-2,-2,2,2] pour les bornes du domaine, 100 pour le nombre de points, 0.1 pour le pas d’intégration et 10x10 points pour le champ de vecteurs.

Question 1 Quels sont les phénomènes et objets géométriques observés ? Que se passe-t-il si le point initial est choisi sur le cercle limite ? Et si on le choisit dans le voisinage du cercle ?

Changeons le signe de epsilon (prendre 150 pour le nombre de points et 0.05 pour le pas).

Question 2 Qu’observe-t-on ? Que peut-on en déduire quant à la robustesse du système pour epsilon=0 ?

2 L’attracteur de Lorenz

2.1 Les équations du système de Lorenz

Nous allons à présent étudier le système différentiel suivant :

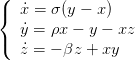( { x˙= σ(y − x) y˙= ρx − y − xz ( z˙= − βz + xy
(2)

2.2 Visualisation de l’attracteur de Lorenz sous Scilab

Nous verrons qu’en traçant la trajectoire 3D de solutions de ce système, nous observons un attracteur de Lorenz.

Dans un fichier lorenz.sci, écrire la fonction qui à (x,y,z) associe (ẋ,ẏ,ż).

Après avoir fait un getf lorenz.sci, utiliser ode pour obtenir la solution du système. On prendra σ = 10, ρ = 28 et β = 12.5∕3. En ce qui concerne la durée de simulation, on prendra un temps long (minimum 20) par pas de 0.01 par exemple. On pourra tester plusieurs états initiaux, comme par exemple (1E-8,1E-8,1E-8) ou (-3,-6,12).

Attention! On ne touche pas au fichier lorenz.sci. On donne les valeurs des constantes dans la ligne de commande Scilab (ou dans le fichier script).

Enfin, tracer le résultat à l’aide de la fonction param3d. On pourra également tracer des projections suivant un axe de coordonnées à l’aide d’un simple plot2d.

Question 3 Faire varier le paramètre β. Qu’observe-t-on ?

Remarque : Il existe sous Scilab une macro, lotest(), qui permet directement de voir l’attracteur de Lorenz. Lancer attractors() pour la charger en mémoire.

3 Évolution d’un attracteur en fonction d’un des paramètres du système

3.1 De quoi s’agit-il ?

Si l’on fait tourner un modèle de population à 2 variables sur plusieurs milliers d’itérations, et que l’on trace son portrait de phase, on va obtenir des points dans le plan correspondant aux valeurs prises par le couple de variables au cours de ces milliers d’itérations. On peut penser a priori que l’on obtiendra des milliers de points (permettant de deviner l’attracteur du système). Le but de ce TD est de répéter cette manipulation en faisant varier un des paramètres du modèle, et d’observer ainsi comment évolue le nombre de points du portrait.

3.2 Quel est le modèle utilisé ?

Le modèle considéré ici est un modèle de population à temps discret et à deux variables

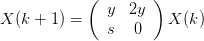( ) X (k + 1) = y 2y X (k ) s 0
(3)

avec

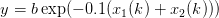y = bexp(− 0.1(x1(k) + x2(k)))
(4)

On prend s = 0.9 et b variable. Nous appellerons ce modèle fish.

Deux autres versions de ce modèle vont être utilisées, correspondant au modèle fish auquel on ajoute un bruit. On définit ainsi fishr

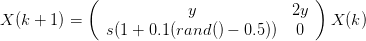( ) y 2y X (k + 1 ) = s(1 + 0.1(rand() − 0.5)) 0 X (k)
(5)

et le modèle fishr2

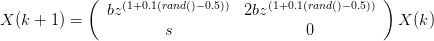( (1+0.1(rand()−0.5)) (1+0.1(rand()−0.5))) X (k + 1) = bz 2bz X (k) s 0
(6)

avec

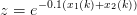z = e− 0.1(x1(k)+x2(k))
(7)

3.3 Simulation sous Scilab

Il existe sous Scilab une macro regroupant l’ensemble des modèles ci-dessus et dénommée bifurcfish. Pour la charger en mémoire, il suffit de taper attractors(). Cette fonction bifurcfish prend pour seul argument le nom du modèle (fish par défaut), et réalise alors automatiquement le diagramme d’évolution de l’attracteur du modèle choisi.

Lancer bifurcfish(). Les portraits de phase défilent les uns derrière les autres.

Question 4 Quel phénomène constate-t-on pour certaines valeurs du paramètre b ?

Ce phénomène d’attraction mis à jour, lancer à présent bifurcfish(fishr) et
bifurcfish(fishr2).

Question 5 Le phénomène est-il encore présent ?