Modèles biologiques et chimiques
Les questions

Stéphane Binois
(last modification date: October 10, 2017)
Version pdf de ce document
Version sans bandeaux

1 Modèle de bioréacteur
2 Un modèle proie-prédateur
3 Un modèle de compétition
4 Réactions en chaîne

Contents

1 Modèle de bioréacteur
2 Un modèle proie-prédateur
 2.1 Équations du modèle
 2.2 Étude du modèle proie-prédateur avec Scilab
  2.2.1 k infini
  2.2.2 k fini
  2.2.3 Retour à k infini
3 Un modèle de compétition
 3.1 Qu’est-ce qu’un modèle de compétition ?
 3.2 Simulation du modèle de compétition
4 Réactions en chaîne
 4.1 Équations de cinétique chimique
 4.2 Simulation de la réaction sous Scilab

1 Modèle de bioréacteur

PIC

Figure 1: Schéma du bioréacteur

Un bioréacteur est constitué d’une cuve où interagissent de la biomasse (cellules vivantes) et du nutriment (sucre). Un flux de débit D l’alimente en nutriment et en retire les produits.

Pour écrire les équations de bilan de masse, on suppose les concentrations uniformes à l’intérieur du bioréacteur et on introduit les variables suivantes :

Les équations du bilan de masse s’écrivent alors

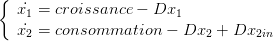{ ˙x = croissance − Dx 1 1 ˙x2 = consommation − Dx2 + Dx2in
(1)

Pour les compléter, nous introduisons les lois de conversion entre biomasse et nutriments. Croissance et consommation sont proportionnelles à la biomasse, le coefficient dépendant uniquement de la concentration en sucre (et pas du temps). On introduit le taux spécifique de croissance

--x2--- μ = 1 + x2 .
On obtient finalement le modèle d’état
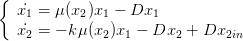{ ˙x1 = μ(x2)x1 − Dx1 ˙x2 = − kμ(x2)x1 − Dx2 + Dx2in
(2)

Nous allons pouvoir agir sur le débit, le coefficient k ainsi que sur la concentration en sucre en entrée x2in.

Notons que ce modèle pourrait être appliqué, en augmentant le nombre de variables de biomasse, à la modélisation de la digestion des boues dans les bassins de décantation.

Ce modèle est l’objet de la macro bioreact. Elle est chargée en mémoire en lançant biosystems() et ses paramètres peuvent être choisis grâce à la fonction bio_init().

A l’aide de la commmande portrait(bioreact), visualiser le champ de vecteurs et quelques trajectoires (domaine [0,0,5,5], 100 points, pas de 0.1 et 10x10 points pour le champ de vecteurs).

Question 1 Combien y a-t-il de points d’équilibre ?

N.B. : Les coordonnées peuvent être obtenues, soit en tapant xclick() dans la ligne de commande et en cliquant sur le point que l’on pense être point d’équilibre, soit en utilisant la fonction fsolve qui cherche le zéro du champ :
deff(’[y]=fsol(x)’,’y=bioreact(t,x)’);
t=0;
fsolve([0;1],fsol)

Question 2 Trouver la stabilité des points d’équilibre en utilisant la macro tangent pour obtenir le linéarisé tangent.

Question 3 Changer progressivement la valeur du débit (qui est une commande du système) en tapant debit=... et observer l’évolution des points d’équilibre.

Question 4 Vérifier théoriquement ces résultats.

2 Un modèle proie-prédateur

2.1 Équations du modèle

Nous considérons dans cette partie une dynamique proie-prédateur d’équations

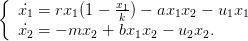{ x˙1 = rx1 (1 − xk1) − ax1x2 − u1x1 x˙2 = − mx2 + bx1x2 − u2x2.
(3)

x1 modélise la proie et x2 le prédateur. La commande u = (u1,u2) correspond à l’effet de l’homme sur la dynamique de chacune des deux espèces (chasse, insecticide...). Il est bien évidemment possible de changer la valeur de chacun des paramètres de ces équations.

2.2 Étude du modèle proie-prédateur avec Scilab

Nous allons utiliser la macro p_p (qui est l’implémentaion du système dynamique décrit ci-dessus), ainsi qu’equilpp, macro qui calcule le point d’équilibre du système dans le quadrant positif ou nul. Ces macros sont chargées en mémoire par l’appel de la macro biosystems(), et les paramètres du système sont initialisés par la macro bio_init().

2.2.1 k infini

Nous nous plaçons dans un premier temps dans le cas k infini (sous Scilab, donner la valeur %inf au paramètre k_pp) et u identiquement nul.

Question 5 Quel est le point d’équilibre du système ? Quel est le comportement du système ? Retrouver le premier résultat à l’aide de la macro equilpp (taper equilpp() ou equilpp([0;0])). Choisir alors un cadre convenable dans portrait(p_p). On prendra un pas d’intégration de 1.

Prenons à présent u strictement positif et tel que u1 = u2.

Question 6 Comment se déplace le point d’équilibre lorsque u croît ? Commenter.

N.B. : Attention, u étant un des arguments de la macro p_p, le portrait de phase s’obtient par la commande portrait(list(p_p,u)) où u a la valeur numérique souhaitée.

Pour certaines valeurs de u, le point d’équilibre est à composante négative. Pour obtenir des points d’equilibre à composante négative, il faut appeler equilpp avec 2 arguments, le premier étant la commande ue, le deuxième pouvant avoir n’importe quelle valeur (la seule présence d’un second argument autorise les points d’équilibre à composante négative).

Question 7 Commenter.

2.2.2 k fini

Reprenons l’étude avec k fini.

Question 8 En quoi le comportement qualitatif du système diffère-t-il du cas précédent ?

Question 9 Que se passe-t-il si l’on prend des composantes différentes dans u (comme par exemple une des deux nulle) ? Quels sont les effets sur l’espèce la plus tuée ? Et les répercussions sur l’autre espèce ?

On considère un cas où le point d’équilibre est positif. Utilisons la macro tangent pour définir un champ de vecteurs linéaire pplin qui représente la dynamique linéarisée autour du point d’équilibre fixé. La syntaxe est [f,g,pplin]=tangent(’p_p’,equilpp(ue),ue). On pourra faire cette question à la main pour plus de précision sur les valeurs propres.

Question 10 Peut-on conclure sur la stabilité du point d’équilibre ?

2.2.3 Retour à k infini

Soit xe le point d’équilibre précédent. On pose :

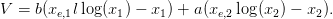V = b(xe,1llog(x1) − x1) + a (xe,2log(x2) − x2).
(4)

Question 11 Comment évolue au cours du temps la quantité V ? Conclure sur la stabilité du point d’équilibre.

Superposons les champs p_p et pplin autour du point d’équilibre retenu. On fera attention au moment de l’appel de portrait à utiliser list(pplin,ue).

Question 12 Visualiser quelques trajectoires. Commenter.

3 Un modèle de compétition

3.1 Qu’est-ce qu’un modèle de compétition ?

Un tel système modélise la dynamique de deux populations vivant sur une même ressource. Ce peut être le cas par exemple de deux souches de levure, ou encore de crustacés sur une algue. Ce système a pour équations

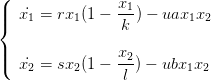( || x˙1 = rx1 (1 − x1) − uax1x2 { k | |( x˙2 = sx2 (1 − x2) − ubx1x2 l
(5)

où 1/u est le niveau de ressources et r,s,k,l,a,b des paramètres que l’on peut faire varier (attention : ces paramètres sont notés r_compet, s_compet, etc... sous Scilab. Seule u possède le même nom u).

Nous allons utiliser ce modèle pour appliquer les concepts de commande et d’observateur.

3.2 Simulation du modèle de compétition

On utilise ici la macro compet, qui est l’implémentation du modèle de compétition, ainsi que equilcom, qui calcule les coordonnées du point d’équilibre en fonction de la commande u (inverse du niveau de ressource). Toutes deux sont chargées grâce à biosystems(), et compet est initialisée à l’aide de bio_init().

Question 13 Calculer le point d’équilibre pour u = 1 (valeur par défaut). Vérifier avec equilcom. Choisir alors un cadre convenable pour tracer le champ de vecteurs grâce à la commande portrait(list(compet,1)). Visualiser quelques trajectoires. Interpréter.

Question 14 Observer le déplacement du point d’équilibre et la modification du champ de vecteurs lorsque u varie. Commenter.

Question 15 Calculer le linéarisé tangent au point d’équilibre du système compet. On pourra utiliser la commande [f,g,complin]=tangent(’compet’,equilcom(ue),ue). Tester la commandabilité et l’observabilité du linéarisé à l’aide de la commande contr(f,g). Visualiser le champ de vecteurs du linéarisé tangent nommé complin.

On pourra se reporter à la partie “Automatique” pour simuler le bouclage de ce système.

4 Réactions en chaîne

4.1 Équations de cinétique chimique

L’objectif de ce TP est d’observer l’évolution des concentrations des réactifs et des produits d’une réaction en chaîne.

Nous considérons donc les réactions (d’ordre 1) A → B → C de constantes k1 et k2.

On peut alors écrire les différentes équations cinétiques :

(| ˙ { [A ] = − k1[A ] [B˙] = k1[A] − k2[B ] |( [C˙] = k2[B]
(6)

ce qui peut se résoudre analytiquement. On obtient ainsi les formules suivantes :

( [A ](t) = A e− k1t { -0k1A0- −k1t −k2t ( [B ](t) = k2−k1e + (k2B0 − k1(B0 + A0))e [C ](t) = A0 − [A](t) − [B ](t)
(7)

4.2 Simulation de la réaction sous Scilab

Question 16 En écrivant les fonctions dans un fichier approprié et les commandes dans un autre fichier, simuler l’évolution des concentrations des trois espèces chimiques en partant des expressions théoriques de ces concentrations (système 7). On pourra prendre A0 = 1, B0 = C0 = 0, k1 = 10 et k2 = 1. (Un bon temps de simulation est alors tf=6).

Question 17 Implémenter le système dynamique (système 6).

Question 18 Tracer l’évolution des concentrations selon les deux systèmes précédents. Tracer également les différences entre les résultats des deux systèmes.

Question 19 Reprendre la simulation en faisant varier les concentrations initiales ainsi que les constantes de réaction.