Modèles multi-espèces de pêche
Les questions

Michel de Lara et Mohamed Sbai
(last modiﬁcation date: October 10, 2017)

Version pdf de ce document
Version sans bandeaux

1 Introduction
2 Le modèle SSVPA (Single Species Virtual Population Analysis)
3 Simulation pour une population de hareng
4 Le modèle MSVPA (Multi Species Virtual Population Analysis)
5 Simulation pour une population de merlu-anchois

1 Introduction

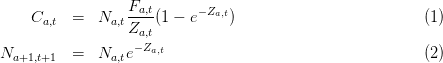
L’approche écosystémique de la gestion des pêches est en plein développement et il est de plus en plus nécessaire de disposer de modèles de poissons ﬁables et qui rendent bien compte de l’évolution des populations marines.

On s’intéresse ici aux modèles multi-espèces de poissons exploités par la pêche. Actuellement, ces modèles sont principalement utilisés dans la mer du Nord et la mer Baltique.

2 Le modèle SSVPA (Single Species Virtual Population Analysis)

Développé par Gulland (1965), ce modèle structuré en âge ne rend pas compte des interactions entre diﬀérentes espèces.
On représente par N_a,t le nombre d’individus d’âge a au début de la période [t,t + 1[ (généralement une année ou un trimestre) et C_a,t le nombre d’individus capturés (par la pêche) sur la période [t,t + 1[. Les 2 équations fondamentales de la SSVPA sont :

Fa,t Ca,t = Na,t----(1 − e−Za,t) (1) Za,t Na+1,t+1 = Na,te−Za,t (2)

avec Z_a,t la mortalité entre t et t + 1 des individus d’âge a. On a:

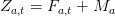Za,t = Fa,t + Ma

(3)

où

M_a est la mortalité naturelle, donnée extérieure au problème;
F_a,t est la mortalité due à la pêche entre t et t + 1.

Pour évaluer le nombre N_0,t+1 d’individus d’âge 0 au début de la période [t + 1,t + 2[, on utilise la relation de stock-recrutement de Ricker :

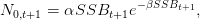− βSSBt+1 N0,t+1 = αSSBt+1e ,

(4)

avec

α et β : paramètres de la relation stock-recrutement de Ricker (constantes) ;
SSB_t+1 : la biomasse féconde en ﬁn de période [t,t + 1[ calculée en sommant la contribution de tous les individus à la reproduction (sauf ceux d’âge 0) :
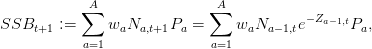$A A ∑ ∑ − Za− 1,t SSBt+1 := waNa,t+1Pa = waNa −1,te Pa, a=1 a=1$ (5)

où
- w_a est le poids aux âges
- P_a est la proportion de reproducteurs aux âges

On veut écrire ce modèle sous forme de modèle d’état. Le vecteur d’état qu’on prend représente le stock :

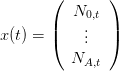
( ) N0,t x(t) = |( ... |) NA,t

et le vecteur commande l’eﬀort de pêche :

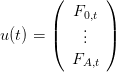
( ) F0,t u (t) = |( ... |) FA,t

A partir de (2) et (4) on trouve que :

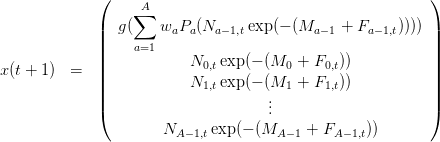( ) ∑A | g( waPa (Na− 1,texp(− (Ma −1 + Fa−1,t)))) | || a=1 || | N0,texp (− (M0 + F0,t)) | x(t + 1) = || || || N1,texp (− (M1 + F1,t)) || ( ... ) N exp(− (M + F )) A− 1,t A−1 A−1,t

(6)

avec

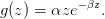
g (z ) = αze −βz.

Il s’agit bien d’une équation dynamique de la forme

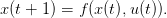
x(t + 1) = f(x(t),u(t)).

3 Simulation pour une population de hareng

Dans cette partie, on va simuler l’évolution d’une population de hareng de la mer du Nord sur un horizon ﬁni.
Le hareng est à dix classes d’âge. Le vecteur d’état qu’on prend est :

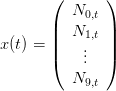
( ) N0,t | N1,t | x (t) = || . || ( .. ) N9,t

D’après ce qui précède, on a l’équation dynamique suivante :

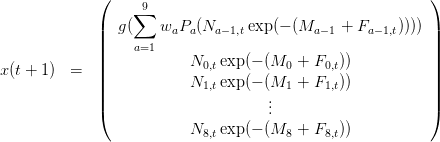
( ∑9 ) | g( waPa (Na− 1,texp(− (Ma −1 + Fa−1,t)))) | | a=1 | || N exp (− (M + F )) || x(t + 1) = || 0,t 0 0,t || | N1,texp (− (M1 + F1,t)) | |( ... |) N exp (− (M + F )) 8,t 8 8,t

avec g(z) = αze^−βz.

Ouvrir un ﬁchier ssvpa.sce et y recopier les données numériques suivantes:

  //etat initial
  X0=[59136429;15134341;16157668;12683928;6271295;3193827;1317572;453613;298854;101254];
  //poids aux âges
  W=[0.007;0.023;0.035;0.051;0.065;0.059;0.075;0.079;0.087;0.094];
  //Proportion mature
  P=[0.00;0.00;0.70;0.90;1.00;1.00;1.00;1.00;1.00;1.00];
  //mortalité par pêche constante
  F=[0.00;0.05;0.14;0.21;0.45;0.30;0.38;0.40;0.39;0.39];
  //coeff de Ricker
  alpha=140.9725694;bbeta=0.00000081;
  //mortalité naturelle
  M=0.2;
  //horizon fini
  T=15;

On écrit la fonction de la dynamique. Pour cela, on écrit d’abord la fonction qui donne la biomasse féconde.

  //biomasse féconde
  function y=Bf(x)
    y=sum(P .*W .*x)
  endfunction
  // on a P(1)=0, de sorte que la somme ne porte que sur les individus matures

  //fonction dynamique
  function y=dyn(k,x)
    e=exp(-M-F);
    y(2:10)=x(1:$-1) .*e(1:$-1);
    z=[0;y(2:$)];
    y(1)=alpha*Bf(z)*exp(-bbeta*Bf(z));
  endfunction

Dans notre modèle, la biomasse B d’une espèce donnée s’écrit :

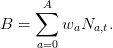∑A B = waNa,t. a=0

(7)

Question 1 Représenter l’évolution de la biomasse. On utilisera la commande plot2d2.

  y=ode("discrete",X0,1,1:T,dyn);
  B=W'*y;// biomasse

  xbasc(0);
  xset("window",0)
  plot2d2(1:T,B)
  xtitle('biomassehareng','temps(annee)','biomasse(kg)')

Figure 1: Evolution de la biomasse du hareng

Question 2 Répéter la même opération pour diﬀérentes valeurs de l’horizon (T=20 et T=50) et de l’eﬀort de pêche. Commenter.

4 Le modèle MSVPA (Multi Species Virtual Population Analysis)

Cette fois, on intègre les interactions entre diﬀérentes espèces dans la modélisation en distinguant dans la mortalité naturelle un terme dû à la prédation. On garde les mêmes notations en ajoutant l’indice i(i =, 1..,n) pour distinguer entre les diﬀérentes espèces:

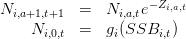Ni,a+1,t+1 = Ni,a,te−Zi,a,t Ni,0,t = gi(SSBi,t)

(8)

où g_i est la fonction de recrutement pour l’espèce i, par exemple (mais pas forcément) la relation de stock-recrutement de Ricker

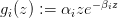
−βiz gi(z) := αize

et avec

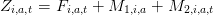
Zi,a,t = Fi,a,t + M1,i,a + M2,i,a,t

où

F_i,a,t est la mortalité due à la pêche pour l’espèce i entre t et t + 1;
M_2,i,a,t est la mortalité par prédation entre t et t + 1;
M_1,i,a est la mortalité ”résiduelle” pour l’espèce i, englobant toutes les autres causes de mortalité et prise comme donnée extérieure au problème comme en SSVPA.

En prenant un vecteur d’état de la forme

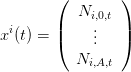
( ) Ni,0,t xi(t) = |( .. |) . Ni,A,t

comme en SSVPS on ne peut pas avoir un modèle d’état.

On prend alors pour vecteur d’état le vecteur de vecteurs

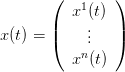
( 1 ) | x (t)| x(t) = ( ... ) xn(t)

Pour l’espèce i, on a d’après (8)

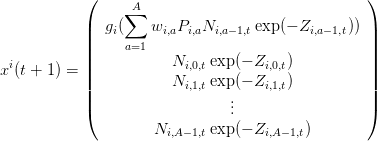( ) ∑A | gi( wi,aPi,aNi,a−1,texp (− Zi,a−1,t))| || a=1 || i | Ni,0,texp(− Zi,0,t) | x (t + 1) = || N exp(− Z ) || || i,1,t . i,1,t || ( .. ) Ni,A− 1,texp(− Zi,A−1,t)

(9)

Par rapport au modèle précèdent, le nouveau terme M_2,i,a,t couple les diﬀérentes équations d’état étant donné qu’il s’exprime en fonction de la biomasse de toutes les autres espéces. En eﬀet, pour un prédateur, on a M₂ = 0 et pour une proie p d’âge b on a :

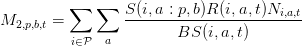
∑ ∑ S(i,a : p,b)R (i,a, t)Ni,a,t M2,p,b,t = ------------------------- i∈𝒫 a BS (i,a,t)

avec

𝒫 l’ensemble des prédateurs;
S(i,a : p,b) le coeﬃcient qui dénote la convenance d’une proie p d’âge b en tant que nourriture pour un prédateur i d’âge a;
R(i,a,t) la quantité d’aliments consommés au temps t par le prédateur i d’âge a.
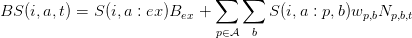
BS(i,a,t) la biomasse de toutes les proies d’un prédateur i d’âge a au temps t; si on note par 𝒜 l’ensemble des proies alors : $∑ ∑ BS (i,a,t) = S(i,a : ex)Bex + S(i,a : p,b)wp,bNp,b,t p∈𝒜 b$ où
- B_ex est la biomasse externe, c’est à dire la biomasse totale de l’écosystème privée de la biomasse des espèces incluses dans le modèle.
- S(i,a : ex) est le coeﬃcient qui dénote la convenance de la biomasse externe en tant que nourriture pour le prédateur i d’âge a

On pose uⁱ(t) = ( )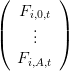
Fi,0,t
| .. |
( . )
Fi,A,t et on déﬁnit le vecteur commande par u(t) = ( )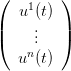
u1(t)
| .. |
( . )
un(t)
Pour simpliﬁer, on suppose que R(i,a,t) est indépendante du temps.

On développe l’expression de M2; on trouve que pour une espèce i, la mortalité est de la forme :

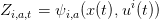
i Zi,a,t = ψi,a(x (t),u (t))

En posant

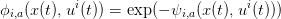
ϕi,a(x (t),ui(t)) = exp(− ψi,a(x(t),ui(t)))

l’équation (9) devient

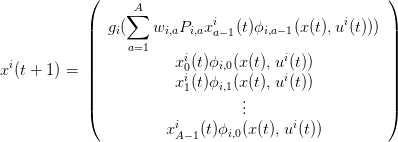( ) ∑A i i || gi( wi,aPi,axa−1(t)ϕi,a−1(x(t),u (t))) || | a=1 | xi(t + 1) = || xi0(t)ϕi,0(x(t),ui(t)) || || xi1(t)ϕi,1(x(t),ui(t)) || | .. | ( . ) xiA−1(t)ϕi,0(x(t),ui(t))

(10)

Soit h_i,a la fonction

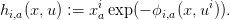hi,a(x,u) := xia exp(− ϕi,a(x,ui)).

(11)

On peut écrire que

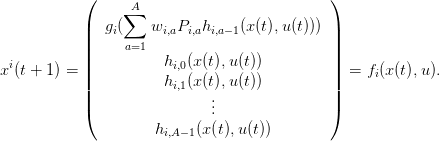
( ) ∑A || gi( wi,aPi,ahi,a−1(x(t),u(t))) || | a=1 | i || hi,0(x(t),u(t)) || x (t + 1) = || hi,1(x(t),u(t)) || = fi(x(t),u). | . | ( .. ) hi,A−1(x(t),u(t))

Finalement on obtient une équation dynamique de la forme voulue

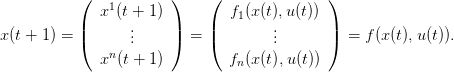
( ) ( ) x1(t + 1) f1(x(t),u(t)) | .. | | .. | x (t + 1) = ( . ) = ( . ) = f (x(t),u (t)). xn (t + 1) fn(x(t),u(t))

5 Simulation pour une population de merlu-anchois

En s’inspirant de la population marine du Golfe de Gascogne, on considère l’écosystème suivant composé d’un prédateur et d’une proie :

merlu (prédateur) à 3 classes d’âge; on adopte la notation N_a,t^m,a = 0, 1, 2 pour désigner le nombre d’individus d’âge a au temps t;
anchois (proie) à 2 classes d’âge (N_a,t^an,a = 0, 1).

Le vecteur d’état est :

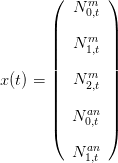
( ) N m0,t | | || N m1,t || || || x (t) = | N m2,t | || || || N an || ( 0,t ) an N 1,t

On suppose que la mortalité par pêche dépend de deux variables de contrôle u(t) et v(t) :

le multiplicateur de mortalité par pêche des merlus F_a,t^m = u(t)F_a^m;
le multiplicateur de mortalité par pêche des anchois F_a,t^an = v(t)F_a^an.

D’après ce qui précède qu’on aboutit à l’équation dynamique

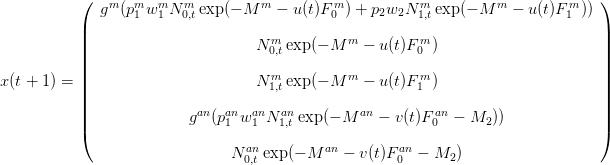
( gm (pm wm N m exp(− M m − u(t)F m ) + p w N m exp(− M m − u(t)Fm )) ) 1 1 0,t 0 2 2 1,t 1 || m m m || || N0,texp(− M − u (t)F 0 ) || | m m m | x(t + 1) = || N1,texp(− M − u (t)F 1 ) || || || | gan(pa1nwan1 N a1n,t exp (− M an − v(t)F a0n− M2 )) | ( ) N a0n,t exp (− M an − v(t)F a0n − M2 )

avec

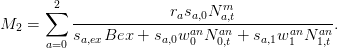
∑2 rasa,0N ma,t M2 = ----------------an--an--------an--an. a=0sa,exBex + sa,0w0 N 0,t + sa,1w 1 N 1,t

Elle est de la forme x(t + 1) = f(x(t),u(t),v(t)).

On suppose u(t) et v(t) constants. Pour le merlu (prédateur), on utilise la relation de stock-recrutement de Ricker

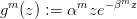m m −βmz g (z) := α ze

(12)

mais, pour l’anchois, on n’utilise pas la relation de stock-recrutement de Ricker. En eﬀet, l’anchois est une espèce qui est très sensibles aux ﬂuctuations environnementales (climat) à court terme ; on considère que le recrutement varie aléatoirement autour d’une valeur moyenne :

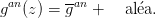gan(z) = gan + al´ea.

(13)

Charger dans un ﬁchier merlu_anchois.sce les données numériques suivantes

  //etat initial
  X0=[82764000;26548000;41440000;18220000;4264000];
  //poids aux ages
  W=[0.004;0.037;0.106;0.012;0.016];
  //proportion mature
  Pm=[0;0;1;0;1];
  //mortalite residuelle
  M1=0.2;
  //quantite d'aliments manges par les merlus aux ages
  R=[1;1.2;1.4];
  //coeff de la relation de Ricker
  alpham=8.745;betam=0.00000000143;
  //valeur moyenne de recrutement pour les anchois
  recrumoya=1500000000;
  //tableau des coef. de suitability
  suit=[0,0,1;0.25,0.15,0.6;0.185,0.385,0.43];
  F1=0.2;
  F2=0.3;
  F4=0.5;
  //biomasse externe
  Bex=10000000;
  //multiplicateurs de mortalité
  u=[1.22;2.35;0.856];

Recopier dans le même ﬁchier les fonctions de mortalité par pêche M2 et de biomasse féconde pour le merlu.

  //mortalité par pêche
  function y=M2(x)
    y=(suit(1,1)*R(1)*x(1))/(suit(1,3)*Bex+suit(1,1)*W(4)*x(4)+suit(1,2)*W(5)*x(5))+ ...
      (suit(2,1)*R(2)*x(2))/(suit(2,3)*Bex+suit(2,1)*W(4)*x(4)+suit(2,2)*W(5)*x(5))+ ...
      (suit(3,1)*R(3)*x(3))/(suit(3,3)*Bex+suit(3,1)*W(4)*x(4)+suit(3,2)*W(5)*x(5))
  endfunction

  //biomasse féconde pour le merlu
  function y=Bfm(x)
    y=Pm(2)*W(2)*x(2)+Pm(3)*W(3)*x(3)
  endfunction

On écrit à la suite la fonction qui donne la dynamique f du modèle merlu_anchois.

  //dynamique
  function y=dyn(k,x)
    y(2)=x(1)*exp(-M1-u(1)*F1)
    y(3)=x(2)*exp(-M1-u(2)*F2)
    y(1)=alpham*Bfm(y)*exp(-betam*Bfm(y))
    y(4)=recrumoya*(1+0.5*(rand()-0.5))
    //   y(4)=300*x(5)*W(5)
    y(5)=x(4)*exp(-M1-u(3)*F4-M2(x))
  endfunction

Question 3 Représenter l’évolution de la biomasse de chacune des deux espèces avec la commande plot2d2.

  y=ode("discrete",X0,1,1:T,dyn);
  Bm=W(1:3)'*y(1:3,:)
  xbasc(0);
  xset("window",0)
  plot2d2(1:T,Bm)
  xtitle('biomassemerlu','temps(annee)','biomasse(kg)')

  Ba=W(4:5)'*y(4:5,:)
  xbasc(1);
  xset("window",1)
  plot2d2(1:T,Ba)
  xtitle('biomasseanchois','temps(annee)','biomasse(kg)')

Figure 2: Evolution de la biomasse des merlus

Figure 3: Evolution de la biomasse des anchois

Question 4 Répéter la même opération pour diﬀérentes valeurs de u et de l’horizon (T=20 et T=30). Commenter.

References

[1] Kjartan G.Magnusson, An overview of the multispecies VPA - theory and applications, Reviews in Fish Biology and Fisheries, 5 195-212 (1995).

[2] H.Gislason Single and Multispecies reference points for Baltic ﬁsh stocks, ICES Journal of Marine Science, 56: 571-583. 1999

[3] H.Gislason, Th.Helgason, Species interaction in assesment of ﬁsh stocks with special application to the North Sea, Dana, vol.5, pp.1-44, 1985.

[4] J. G.Pope, The ICES Multispecies Assesment Working Group: evolution, insights and future problems, ICES mar.Sci.Symp.,193:22-33. 1991.

[5] Report of the Workshop on MSVPA in the North SEA, Charlottenlund, Denmark 8-12 avril 2002.

[6] Sparre.P, Introduction to multispecies virtual population analysis, ICES mar.Sci.Symp.,193:12-21.1991.

[7] Mark Kot, Elements of Mathematical Ecology, Cambridge University Press.

Modèles multi-espèces de pêche Les questions

Contents

1 Introduction

2 Le modèle SSVPA (Single Species Virtual Population Analysis)

3 Simulation pour une population de hareng

4 Le modèle MSVPA (Multi Species Virtual Population Analysis)

5 Simulation pour une population de merlu-anchois

References

Modèles multi-espèces de pêche
Les questions