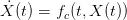
ode est un solveur de systèmes d’équations différentielles ou récurrentes, c’est-à-dire des systèmes du type
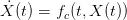 | (1) |
ou
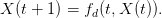 | (2) |
C’est cet outil qui sera utilisé tout au long de ces TD, même sans être nommé (par exemple, la macro portrait l’appelle lorsqu’on lui demande de tracer des trajectoires).
ode demande 4 paramètres obligatoires, à savoir :
La résolution se fait alors par l’appel y=ode(y0,t0,t,fct) en temps continu et y=ode(’discrete’,y0,t0,t,fct) en temps discret. Dans les 2 cas, la matrice y contiendra les valeurs de l’état pour tous les instants inscrits dans le vecteur de temps t.
Prenons un exemple simplissime : considérons le système à une dimension X(t + 1) = X(t) + 1. On veut simuler son évolution sur 10 unités de temps, avec un pas de temps de 0.1, en partant de t0=0 et x0=0. Il nous suffit de définir la fonction f : deff(’[xdot]=f(t,x)’,’xdot=x+1’), de définir x0, t0 et t: x0=0;t0=0;t=0:0.01:10; puis de lancer ode : x=ode(’discrete’,x0,t0,t,f);, et enfin de tracer le résultat plot(t,x).
En ce qui concerne l’utilisation d’ode en temps continu, on pourra se référer directement à l’aide en ligne help ode... ou faire le premier TP, qui concerne un système dynamique linéaire simple.
Lorsque l’on écrit une fonction pour ode, elle doit être de la forme [ydot]=fct(t,y) ou [x(k+1)]=fct(k,x). Ne pas oublier la présence du temps dans les arguments de la fonction, sinon ode refusera de s’exécuter. On peut par contre mettre autant d’arguments que l’on veut après le temps et l’état. On peut en particulier faire figurer une commande externe parmi les arguments. L’appel d’ode se fera alors à l’aide de la macro list : y=ode(y0,t0,t,list(fct,u,...)).
Comme son nom l’indique, portrait trace les portraits de phase. portr3d est quant à lui son équivalent en 3 dimensions. Leur utilisation est des plus simples : si l’on veut le portrait d’une fonction fct du type de celles autorisées par ode, il suffit de taper portrait(fct). Il n’y a plus qu’à se laisser guider par les boîtes de dialogue.
Si toutefois ces boîtes vous ennuient, vous pouvez les court-circuiter en spécifiant vos choix dès la ligne de commande. L’appel devient plus long : portrait(fct,odem,xdim,npts), où odem est le type d’intégration ode souhaité (par défaut c’est ... ’default’), xdim le vecteur du domaine souhaité [xmin,xmax,ymmn,ymax,zmin,zmax] (on s’arrête à ymax pour les portraits en 2 dimensions...) et npts le vecteur [nombre de points,pas d’intégration].
Si la fonction considérée requiert des arguments extérieurs, on pourra utiliser l’appel portrait(list(fct,u,...)).
Cette macro trace le champ de vecteurs d’un système. Son appel est simple : fchamp(fct,t,xr,yr) où fct est le système en question, t auquel on veut tracer le champ, (xr,yr) deux vecteurs colonnes définissant les coordonnées des points où seront calculés les vecteurs du champ.
Cette macro renvoie le zéro d’un champ de vecteurs y=fct(x). L’appel se fait par x=fsolve(x0,fct). Notons que l’appel [x,v]=fsolve(x0,fct) renvoie le zéro et la valeur de la fonction de champ en ce point.
tangent permet de linéariser un système dynamique autour d’un point d’équilibre. Elle prend comme arguments le nom de la fonction qui code le système, fct, le point d’équilibre xe et éventuellement la commande ue. Elle renvoie les deux matrices f et g du linéarisé, telles que dxdot=f.dx + g.du, ainsi qu’une macro codant le système linéarisé sysl.
L’appel se fait par [f,g,sysl]=tangent(fct,xe,ue).