In order to correlate the assets we assume that
![]() is a vector of independent Brownian
motions, that
is a vector of independent Brownian
motions, that ![]() is a
is a ![]() matrix, and we define
matrix, and we define
![]() by
by
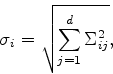
![\begin{displaymath}
\bar{W}^i_t = \frac{[\Sigma W_t]_i}{\sigma_i}
= \frac{\sum_{j=1}^d \Sigma_{ij} W^j_t}{\sigma_i}.
\end{displaymath}](img9.png)
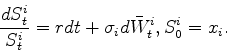
Note that
![]() , where
, where
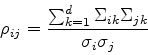
Compute, using a Monte-Carlo method, the price of a call
whose payoff is given at time ![]() by
by
Do the same computation for an index put whose payoff is given by
![]() .
.
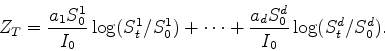
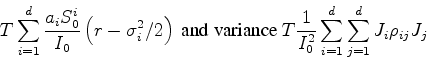
We recall the following formula (Black-Scholes formula, exercise)
Use this formula to give an explicit expression to
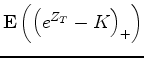 and propose
a control variate technique for the computation
of the call option.
and propose
a control variate technique for the computation
of the call option.
Compare this method to the standard one for different values of
![]() .
.
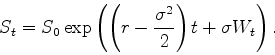
Prove, using simulation, that the relative precision of the
computation decrease when ![]() increase. Take
increase. Take ![]() and
and ![]() ,
,
![]() ,
, ![]() ,
, ![]() . What happen when
. What happen when ![]() ?
?