Autour du modèle de Black et Scholes
On s'intéresse au modèle de Black et Scholes, donné par :
On supposera dans la suite que 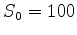 ,
,
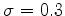 (volatilité annuelle) et
(volatilité annuelle) et 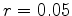 (taux d'intérêt
exponentiel annuel).
(taux d'intérêt
exponentiel annuel).
- Simuler une suite de variables aléatoires gaussiennes centrées
réduites, la trajectoire d'un mouvement brownien et enfin celle d'un
modèle de Black et Scholes.
- Pour un même mouvement brownien, tracer une trajectoire avec
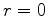 ,
,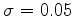 ,
, 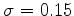 . Ces variations n'ont pas
d'influence sur le prix des options.
. Ces variations n'ont pas
d'influence sur le prix des options.
De même, tracer des trajectoires avec 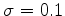 ,
,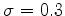 ,
,
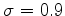 . Ces variations ont une influence sur le prix des
options.
. Ces variations ont une influence sur le prix des
options.
- Implémenter les formules de Black et Scholes pour les puts et les calls.
Nous allons, comme dans le cas du modèle de Black et Scholes,
implémenter une procédure de couverture. La théorie suggère
d'intervenir à tout instant ce qui est bien entendu impossible. Nous
allons intervenir à des pas de temps séparé de 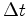 (typiquement
une heure, un jour, un mois).
(typiquement
une heure, un jour, un mois).
Nous chercherons à couvrir un call de strike 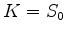 et d'échéance
et d'échéance 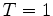 an.
an.
- Pour un pas de temps fixé, implémenter une procédure de
couverture (appliquer par exemple la formule de couverture de
Black-Scholes aux instants
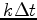 ). On veillera à constituer un
portefeuille autofinancé (la valeur de ce portefeuille est
différente (mais proche) du prix de l'option).
). On veillera à constituer un
portefeuille autofinancé (la valeur de ce portefeuille est
différente (mais proche) du prix de l'option).
- On s'intéresse maintenant au défaut de couverture (la différence
entre la valeur finale du portefeuille et la payoff de l'option).
Simuler, sous la probabilité risque neutre (
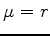 ), ce défaut de
couverture. Tracer en un histogramme et évaluer sa moyenne et son
écart type.
), ce défaut de
couverture. Tracer en un histogramme et évaluer sa moyenne et son
écart type.
- Etudier ces quantités lorsque
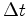 tends vers
tends vers 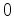 .
On étudiera en particulier les variances stratègies qui consistent :
.
On étudiera en particulier les variances stratègies qui consistent :
- à ne rien faire,
- à se couvrir une fois au début de la période,
- à se couvrir une fois par mois,
- à se couvrir une fois par semaine,
- à se couvrir une fois par jours.
- Répeter les simulations lorsque
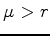 et
et 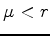 . Que se passe
t'il pour la moyenne ? pour l'écart type ? Quand a t'on intérêt à acheter
des calls ? des puts ?
. Que se passe
t'il pour la moyenne ? pour l'écart type ? Quand a t'on intérêt à acheter
des calls ? des puts ?
- On pourra recommencer cet exercice de couverture, en prennant
une combinaison de put et de call. En voici quelques exemples :
- Bull spread : constituée de l'achat d'un call
de prix d'exercice 90 (abrégé en call 90)
et de la vente d'un call 110 de même échéance.
- Strangle : constituée de la vente d'un put 90
et de la vente d'un call 110.
- Condor : constituée de la vente d'un call
90, de l'achat d'un call 95 et d'un call 105 et
de la vente d'un call 110.
- Put ratio backspread : constituée de la vente d'un put
110 et de l'achat de 3 puts 90.
Nous allons considérer l'exemple du call barrière pour une barrière
plus grande que le strike. Cette option est particulièrement délicate
à couvrir pour des raisons qui apparaitrons plus tard. Un call
barrière promet à sont échéance 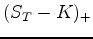 sous réserve que la
trajectoire de
sous réserve que la
trajectoire de 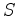 reste inférieure à
reste inférieure à 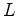 (
(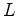 étant une
constante plus grande que
étant une
constante plus grande que 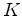 ). Le payoff est donné par :
). Le payoff est donné par :
On peut montrer (moyennant quelques calculs ...) que le prix
à l'instant 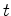 si l'actif vaut
si l'actif vaut 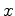 est donné par :
est donné par :
et la couverture par :
- Implementer le prix et la couverture de l'option. Verifier que
lorsque
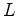 tends vers
tends vers 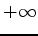 , le prix converge vers le prix du
call classique.
, le prix converge vers le prix du
call classique.
- Tester le procédure de couverture, comme dans le cas d'une
option classique.
- Tracer la courbe
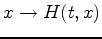 . Vérifier que
. Vérifier que
![$\sup_{t\leq T,x\in
[0,L]} H(t,x) = +\infty$](img30.png) . Est ce bien raisonnable ?
. Est ce bien raisonnable ?
- Nous allons simuler une trajectoire de façon à faire apparaitre
la difficulté (c'est à dire en imposant
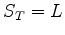 ). Expliquer comment
siumler un mouvement brownien conditionnellement à
). Expliquer comment
siumler un mouvement brownien conditionnellement à 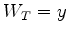 (on
remarquera que
(on
remarquera que
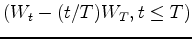 est un processus gaussien
indépendant de
est un processus gaussien
indépendant de 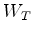 ). En déduire une méthode de simulation de la
trajectoire
). En déduire une méthode de simulation de la
trajectoire 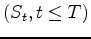 conditionnellement à
conditionnellement à 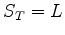 .
.
- Implémenter la procédure de couverture sur cette trajectoire.
Que se passe t'il ?
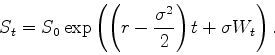
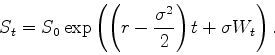
![]() ,
,![]() ,
,
![]() . Ces variations ont une influence sur le prix des
options.
. Ces variations ont une influence sur le prix des
options.
![]() et d'échéance
et d'échéance ![]() an.
an.
![]() sous réserve que la
trajectoire de
sous réserve que la
trajectoire de ![]() reste inférieure à
reste inférieure à ![]() (
(![]() étant une
constante plus grande que
étant une
constante plus grande que ![]() ). Le payoff est donné par :
). Le payoff est donné par :