next_inactive up previous


SCILAB à l'École nationale des ponts et chaussées


http://www.enpc.fr/scilab



Statistique
Modèle linéaire gaussien

Didier CHAUVEAU - Jean-François DELMAS


Date: dernière date de mise à jour : 19 novembre 2003

Version pdf de ce document


Table des matières

1 Peut-on augmenter la quantité de pluie?

1.1 La problématique

Il existe deux types de nuages qui donnent lieu à des précipitations: les nuages chauds et les nuages froids. Ces derniers possèdent une température maximale de l'ordre de -10°C à -25°C. Ils sont composés de cristaux de glace et de gouttelettes d'eau. Ces gouttelettes d'eau subsistent alors que la température ambiante est inférieure à la température de fusion. On parle d'eau surfondue. Leur état est instable. De fait, quand une particule de glace rencontre une gouttelette d'eau, elles s'aggrègent pour ne former qu'une seule particule de glace. Les particules de glace, plus lourdes que les gouttelettes, tombent sous l'action de la gravité. Enfin si les températures des couches d'air inférieures sont suffisamment élevées, les particules de glace fondent au cours de leur chute formant ainsi de la pluie.

En l'absence d'un nombre suffisant de cristaux de glace pour initier le phénomène décrit ci-dessus, on peut injecter dans le nuage froid des particules qui ont une structure cristalline proche de la glace, par exemple de l'iodure d'argent (environ 100 à 1000 grammes par nuage). Autour de ces particules, on observe la formation de cristaux de glace, ce qui permet, on l'espère, de déclencher ou d'augmenter les précipitations. Il s'agit de l'ensemencement des nuages. Signalons que cette méthode est également utilisée pour limiter le risque de grêle.

Il est évident que la possibilité de modifier ainsi les précipitations présente un grand intérêt pour l'agriculture. De nombreuses études ont été et sont encore consacrées à l'étude de l'efficacité de l'ensemencement des nuages dans divers pays. L'étude de cette efficacité est cruciale et délicate. Le débat est encore d'actualité.

1.2 Les données

On dispose des données concernant l'ensemencement par iodure d'argent des nuages en Floride (1975)1.

Les volumes de pluie déversées en $ 10^7 \;$   m$ \quad ^3$ (cf. les deux tableaux ci-dessous) concernent 23 jours similaires dont $ n_1=11$ jours avec ensemencement correspondant aux réalisations des variables aléatoires $ X_1,\ldots ,X_{n_1}$ et $ n_2=12$ jours sans ensemencement correspondant aux réalisations des variables aléatoires $ Y_1,\ldots ,Y_{n_2}$.


Tableau: Volume de pluie en $ 10^7 \;$   m$ \quad ^3$ déversée avec ensemencement
$ i$ 1 2 3 4 5 6 7 8 9 10 11
$ X_i$ 7.45 4.70 7.30 4.05 4.46 9.70 15.10 8.51 8.13 2.20 2.16



Tableau: Volume de pluie en $ 10^7 \;$   m$ \quad ^3$ déversée sans ensemencement
$ j$ 1 2 3 4 5 6 7 8 9 10 11 12
$ Y_j$ 15.53 10.39 4.50 3.44 5.70 8.24 6.73 6.21 7.58 4.17 1.09 3.50 



X=[7.45, 4.70, 7.30, 4.05, 4.46, 9.70, 15.10, 8.51, 8.13, 2.20, 2.16];
Y=[15.53, 10.39, 4.50, 3.44, 5.70, 8.24, 6.73, 6.21, 7.58, 4.17, 1.09, 3.50];
n1 = length(X);
n2 = length(Y);

1.3 Le modèle

On suppose que les volumes de pluies suivent une loi gaussienne et que l'effet de l'ensemencement ne modifie pas la variance des loies gaussiennes.

Ceci revient à dire dans ce contexte paramétrique que les observations sont constituées de deux échantillons gaussiens indépendants

$\displaystyle X_1,\ldots,X_{n_1}$ i.i.d. $\displaystyle {\mathcal N}(\mu_1,\sigma^2),$  
$\displaystyle Y_1,\ldots,Y_{n_2}$ i.i.d. $\displaystyle {\mathcal N}(\mu_2,\sigma^2).$  

On souhaite tester l'hypothèse nulle $ H_0$: ``le procédé n'a pas d'effet'' contre ``le procédé produit une augmentation significative de la quantité de pluie'', autrement dit

$\displaystyle H_0 =\{ \mu_1 = \mu_2 \}$   contre$\displaystyle \quad H_1 =\{ \mu_1 > \mu_2\}. $

Il est indispensable de s'assurer d'abord que les hypothèses de modèle que l'on a faites sont raisonnables:
  1. Les données peuvent-elles être considérées comme des réalisations de lois gaussienne pour les paramètres (moyenne, variance) appropriés?
  2. Peut-on considérer que les variances sont les mêmes?
Des éléments de réponses au point (1) seront abordées au chapitre 3. Le point (2) est abordé dans le paragraphe facultatif 1.5.

Nous admettons donc dans un premier temps ces deux hypothèses.

1.4 Comparaison des moyennes

Afin de se faire une idée des données et de l'écart entre les deux populations, on peut commencer par calculer les moyennes empiriques

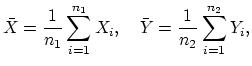
$\displaystyle \bar X = \mathop{\frac{1}{ n_1}}\nolimits \sum_{i=1}^{n_1} X_i, \quad \bar Y = \mathop{\frac{1}{ n_2}}\nolimits \sum_{i=1}^{n_2} Y_i, $

ainsi que les variances empiriques
$\displaystyle S_X^2$ $\displaystyle =$ $\displaystyle \mathop{\frac{1}{ n_1-1}}\nolimits \sum_{i=1}^{n_1} (X_i-\bar X)^... ..._1-1}\left[ \frac{1}{n_1} \sum_{i=1}^{n_1} X_i^2 - \left(\bar X\right)^2\right]$  
$\displaystyle S_Y^2$ $\displaystyle =$ $\displaystyle \frac{1}{n_2-1}\sum_{i=1}^{n_2} (Y_i-\bar Y)^2 = \frac{n_2}{ n_2-1}\left[ \frac{1}{n_2} \sum_{i=1}^{n_2} Y_i^2 - \left(\bar Y\right)^2\right],$  

ou plutôt les écart-types correspondants $ S_X$ et $ S_Y$: 


// calcul des moyennes
mu1=sum(X)/n1
mu2=sum(Y)/n2
// calcul des variances empiriques sans biais
SX2 = n1/(n1-1)*(sum(X.^2)/n1- mu1^2)
SY2 = n2/(n2-1)*(sum(Y.^2)/n2- mu2^2)

    

Question 1   Quelles sont les lois des v.a. $ \bar X$ et $ (n_1-1)S^2_X/\sigma^2$ ? Rappeler la loi de

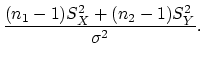
$\displaystyle \frac{(n_1-1)S_X^2 + (n_2-1)S_Y^2}{\sigma^2}. $



    

Question 2   En déduire que sous $ H_0$,

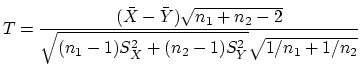
$\displaystyle T = \frac{(\bar X - \bar Y)\sqrt{n_1+n_2-2}}{ \sqrt{(n_1-1)S_X^2 + (n_2-1)S_Y^2} \sqrt{1/n_1 + 1/n_2}} $

suit une loi de Student sous $ H_0$, dont on précisera le paramètre. Quel est le comportement de $ T$ sous $ H_1$, quand $ n_1\rightarrow\infty $, $ n_2\rightarrow\infty $ et $ n_1/n_2\rightarrow \theta\in]0,\infty [$?



    

Question 3   Construire, à partir de la statistique $ T$, un test d'égalité des moyennes. Déterminer la région critique. Calculez la valeur de la statistique de test, la valeur critique, et la $ p$-valeur pour les données de pluie. Conclusion.



On donne les commandes Scilab suivantes concernant la fonction de répartion (``cumulative distribution function'' en anglais) de la loi de Student:

Pour avoir plus d'information sur la fonction cdft, on peut consulter le manuel en utilisant la commande help cdft.


1.5 Comparaison des variances des 2 échantillons gaussiens (FACULTATIF)

Pour s'assurer du point (2), on peut tout d'abord supposer que ces variances sont différentes, i.e.

$\displaystyle X_i$ $\displaystyle \sim$ $\displaystyle {\mathcal N}(\mu_1,\sigma^2_1), \quad i=1,\ldots,n_1,$  
$\displaystyle Y_j$ $\displaystyle \sim$ $\displaystyle {\mathcal N}(\mu_2,\sigma^2_2), \quad j=1,\ldots,n_2,$  

puis construire un test d'égalité des variances, afin de voir si la différence sur les variances (ou les écart-types) observée est significative.

    

Question 4 (Facultatif)   Quelle est la loi de la statistique $ F=S_X^2/S_Y^2$ sous l'hypothèse nulle d'égalité des variances? Quel est son comportement sous $ H_1$, quand $ n_1\rightarrow\infty $ et $ n_2\rightarrow\infty $?



    

Question 5 (Facultatif)   Construire, à partir de la statistique $ F$, un test d'égalité des variances. Déterminer la région critique du test, évaluer la valeur critique et la $ p$-valeur pour les données de pluie? Conclusion.



On donne les commandes Scilab suivantes concernant la fonction de répartion de la loi de Fisher:

Pour avoir plus d'information sur la fonction cdff, on peut consulter le manuel en utilisant la commande help cdff.

2 Analyse de la variance à un facteur

2.1 Les données

On dispose de données (réelles) relatives à 6 jeux de notes pour un même contrôle, corrigé par un unique correcteur, mais concernant six petites classes (et donc six enseignants) différentes. On désire savoir si les résultats des petites classes sont significativement différents.

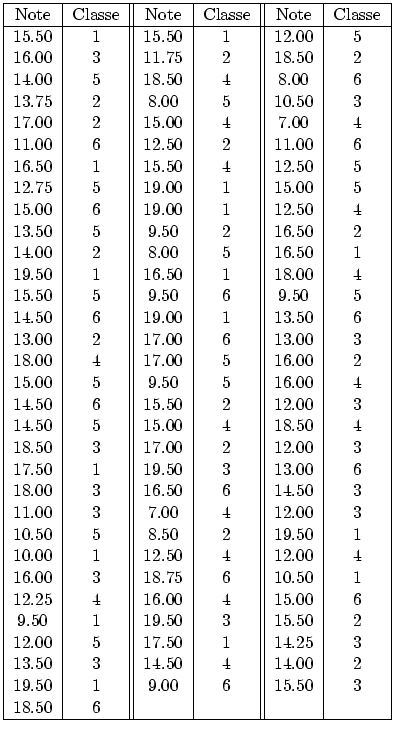
$\displaystyle \begin{tabular}{\vert c\vert c\vert\vert c\vert c\vert\vert c\ver... ....50 & 1 & 9.00 & 6 & 15.50 & 3 \\ 18.50 & 6 & & & & \\ \hline \end{tabular}$

2.2 Le modèle

On fait l'hypothèse que les notes sont distribuées suivant une loi gaussienne de même variance, et de moyenne dépendant de l'enseignant. Le modèle s'écrit donc

$\displaystyle X_{i,j} = m_i + \varepsilon_{i,j},\quad i=1,\ldots,6, \quad j=1,\ldots,n_i, $

où $ m_i$ est la note moyenne (inconnue) liée à l'enseignant $ i$, et les $ \varepsilon_{i,j}$ sont des v.a. indépendantes de loi $ {\mathcal N}(0,\sigma^2)$, où $ \sigma^2>0$ est inconnu également.

    

Question 6   Quelles sont les estimations des $ m_i$, $ i=1,\ldots,6$? Quelle est l'estimation de $ \sigma^2$? 




// données notes
X=[
15.50; 15.50; 12.00; 16.00; 11.75; 18.50; 14.00; 18.50;  8.00; 13.75;
 8.00; 10.50; 17.00; 15.00;  7.00; 11.00; 12.50; 11.00; 16.50; 15.50;
12.50; 12.75; 19.00; 15.00; 15.00; 19.00; 12.50; 13.50;  9.50; 16.50;
14.00;  8.00; 16.50; 19.50; 16.50; 18.00; 15.50;  9.50;  9.50; 14.50;
19.00; 13.50; 13.00; 17.00; 13.00; 18.00; 17.00; 16.00; 15.00;  9.50;
16.00; 14.50; 15.50; 12.00; 14.50; 15.00; 18.50; 18.50; 17.00; 12.00;
17.50; 19.50; 13.00; 18.00; 16.50; 14.50; 11.00;  7.00; 12.00; 10.50;
 8.50; 19.50; 10.00; 12.50; 12.00; 16.00; 18.75; 10.50; 12.25; 16.00;
15.00;  9.50; 19.50; 15.50; 12.00; 17.50; 14.25; 13.50; 14.50; 14.00;
19.50;  9.00; 15.50; 18.50];
// données facteur
Grp=[
1; 1; 5; 3; 2; 2; 5; 4; 6; 2; 5; 3; 2; 4; 4; 6; 2; 6; 1; 4; 5; 5; 1; 5;
6; 1; 4; 5; 2; 2; 2; 5; 1; 1; 1; 4; 5; 6; 5; 6; 1; 6; 2; 6; 3; 4; 5; 2;
5; 5; 4; 6; 2; 3; 5; 4; 4; 3; 2; 3; 1; 3; 6; 3; 6; 3; 3; 4; 3; 5; 2; 1;
1; 4; 4; 3; 6; 1; 4; 4; 6; 1; 3; 2; 5; 1; 3; 3; 4; 2; 1; 6; 3; 6];

N = length(X);
k = max(Grp); // nb de groupes
mg = sum(X)/N; // X..
for i=1:k, n(i) = length(X(Grp==i)); end; // n_i
for i=1:k, moy(i) = sum(X(Grp==i))/n(i); end; // X_i.
[n,moy] // effectif et moyenne de chaque groupe

    

Question 7   Peut-on considérer qu'il existe une différence significative entre les notes des classes, dues aux qualités pédagogiques des enseignants? Effectuer le test de l'hypothèse nulle $ H_0:$ ``les enseignants ne présentent pas de différence'' contre ``c'est faux''. Écrire la table d'analyse de la variance et conclure.



On pourra utiliser les commandes suivantes: 


// calcul des sommes de carres
SSM = sum(n.*(moy-mg).^2); 
SSE = sum((X-moy(Grp)).^2);

    

Question 8 (Facultatif)   Si l'on rejette $ H_0$, il est naturel de déterminer les classes qui sont significativement différentes.
  1. Proposer des intervalles de confiance pour les notes moyennes pour chaque classe.
  2. Proposer un test de l'hypothèse nulle

    $\displaystyle H_0=\{m_i = m_j\}$   contre$\displaystyle \quad H_1=\{m_i \ne m_j\}, $

    fondé sur la loi de Student, et l'utiliser afin de comparer quelques couples de moyennes.



3 Régression linéaire

3.1 Les données

L'exemple utilisé a déjà été proposé dans les exercices sur le chapitre 2. On dispose de données concernant l'âge ($ X_1$), le kilométrage en milliers de kms ($ X_2$), et le prix en milliers d'euros ($ Y$) pour un échantillon de voitures d'occasion d'un même type:

$\displaystyle \begin{tabular}{\vert c\vert c\vert c\vert} \hline $X_1$ & $X_2$ ... ...3& 8.7\\ 2& 13& 15.4\\ 7& 111& 6.4\\ 7& 143& 4.4\\ \hline \end{tabular}$

Si l'on veut étudier la liaison entre les variables potentiellement explicatives et la variable à expliquer (le prix $ Y$), on peut commencer par visualiser les nuages de points $ (X_1,Y)$ et $ (X_2,Y)$: 


clear
donnees = [
5  92  7.8; 4  64  9.5; 6 124  6.4; 5  97  7.5; 5  79  8.1; 5  76  9.0;
6  93  6.1; 6  63  8.7; 2  13 15.4; 7 111  6.4; 7 143  4.4];
// definition des variables
X1=donnees(:,1); X2=donnees(:,2); Y=donnees(:,3);
n=length(Y);
// allures des nuages
xbasc();
subplot(121), plot2d(X1,Y,-2,"111","Age",[1,0,8,16]);
subplot(122), plot2d(X2,Y,-3,"111","Kms",[0,0,150,16]);

    

Question 9   Que suggèrent les deux nuages?



3.2 Régression linéaire simple

On propose tout d'abord le modèle

$\displaystyle Y = \beta + \alpha X_1 + \varepsilon, $

où $ \varepsilon$ est un échantillon de $ {\mathcal N}(0,\sigma^2)$.

    

Question 10   Donner des estimateurs sans biais pour les paramètres $ (\beta,\alpha)$ ainsi que $ \sigma^2$. Ce modèle est-il significatif? (autrement dit, l'âge a-t-il une influence sur le prix?).



On propose ici de définir une fonction qui, à partir de la donnée du modèle sous la forme $ Y = M\theta + \varepsilon$, où $ Y$ est la variable à expliquer et $ M$ la matrice définissant le modèle, calcule les éléments usuels: L'estimateur du paramètre $ \theta$:

$\displaystyle \hat\theta = (M^t M)^{-1} M^t Y, $

et le test portant sur l'hypothèse nulle ``aucun régresseur n'est significatif''. Afin d'imiter les logiciels de statistiques standards, la fonction regression() imprime également la table d'analyse de variance associée au test.

Dans le cas de ce premier modèle à 1 régresseur, la réponse à la question 7 est donc directement donnée par cette fonction, puisque ici elle effectue le test de $ H_0=\{\alpha = 0\}$ contre $ \{\alpha\ne 0\}$. 


function [theta,MSE,pv] = regression(M,Y)
// regression lineaire avec table d'anova
// M = matrice (n,p) des regresseurs, Y = observations (n,1)
// theta = estimateur des parametres
// MSE   = Mean Square Error estimateur de la variance
// pv    = p-valeur du test de Ho : "pas de regresseurs"
[n,p]=size(M);
theta = inv(M'*M)*M'*Y; // estimateur des parametres
// calcul des sommes de carres
YE = M*theta;                 // projete sur E
SSE = sum((Y - YE).^2);       // ||Y-YE||^2
MSE = SSE/(n-p);
SSM = sum((YE - mean(Y)).^2); // ||YE-YH||^2
MSM = SSM/(p-1);
F = MSM/MSE;                      // Fisher
q5 = cdff("F",p-1,n-p,0.95,0.05); // quantile a 5%
[pp,qq] = cdff("PQ",F,p-1,n-p);    
pv=qq; // p-valeur
// Affichage de la table d'anova
printf("\n");
printf("TABLE D''ANALYSE DE LA VARIANCE\n");
printf("Source   SS      DF    MS      Fisher  p-valeur\n");
printf("-----------------------------------------------\n");
printf("Model  %6.1f   %3d  %6.1f    %4.1f    %f\n",...
SSM,p-1,MSM,F,pv);
printf("Error  %6.1f   %3d  %6.1f\n",SSE,n-p,MSE);
printf("-----------------------------------------------\n");
printf("quantile de F(%d,%d) a 95%% : %f\n",p-1,n-p,q5);
endfunction;

Le calcul donne pour notre modèle: 


// MODELE 1 (simple)  Y = b + a X1 + eps
M1 = [ones(n,1) X1]; // matrice des regresseurs
[theta1,MSE1,pv1] = regression(M1,Y);
printf("Estimateurs: b=%f, a=%f\n",theta1(1),theta1(2));
printf("Variance = %f, sigma = %f\n",MSE1,sqrt(MSE1));

On représente enfin la droite de régression sur le nuage: 


xbasc();
// trace de la droite
z=1:0.1:8; t=theta1(1)+theta1(2)*z; xbasc();
plot2d(X1,Y,-2,"111","Age",[1,0,8,16]);
plot2d(z,t,[1],"000");

3.3 Régression linéaire multiple

On propose d'essayer à présent le modèle ``complet''

$\displaystyle Y = \gamma + \alpha_1 X_1 + \alpha_2 X_2 + \varepsilon. $

    

Question 11   Donner des estimations sans biais des paramètres $ (\gamma,\alpha_1,\alpha_2)$ et $ \sigma^2$ (ici, écrire les commandes Scilab nécessaires).



    

Question 12   Test de l'utilité d'un régresseur: Tester, au niveau 5%, l'hypothèse nulle ``le kilométrage n'a pas d'effet sur le prix'' contre ``c'est faux''.



La fonction définie précédemment n'effectue pas le test demandé (quel test effectue-t-elle?). Ecrire les commandes Scilab permettant de calculer la statistique et la $ p$-valeur du test demandé, et conclure.

    

Question 13   Quel modèle explique le mieux le prix?




Notes

... (1975)1
William L. Woodley, Joanne Simpson, Ronald Biondini, Joyce Berkeley, Rainfall results, 1970-1975: Florida Area Cumuls Experiment, Science, Vol 195, pp. 735-742, February 1977.
next_inactive up previous
Jean-Francois Delmas 2003-11-19