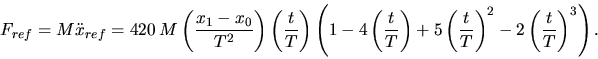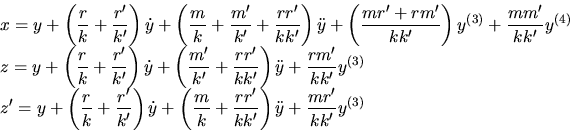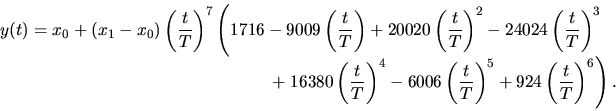


SCILAB à l'École nationale des ponts et chaussées
http://www.enpc.fr/scilab
Modélisation et Commande des Systèmes Non
Linéaires,
ENPC, Département MSPI.
Positionnement de Masses
Reliées Élastiquement à
un Moteur Linéaire
Jean LEVINE
dernière date de mise à jour : 24 avril 2002
On considère dans un premier temps un moteur linéaire de masse 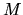 , se
déplaçant le long d'un rail rectiligne, relié à un corps de masse
, se
déplaçant le long d'un rail rectiligne, relié à un corps de masse
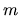 par une tige flexible de masse négligeable que l'on
peut assimiler à un ensemble ressort-amortisseur, le ressort ayant une
raideur
par une tige flexible de masse négligeable que l'on
peut assimiler à un ensemble ressort-amortisseur, le ressort ayant une
raideur 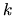 et l'amortisseur un coefficient d'amortissement
et l'amortisseur un coefficient d'amortissement 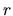 .
L'abscisse du moteur (resp. de la masse) est notée
.
L'abscisse du moteur (resp. de la masse) est notée 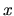 (resp.
(resp. 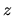 ).
Le moteur produit une force
).
Le moteur produit une force 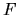 qui est la variable de commande. Le
système s'écrit, en première approximation,
qui est la variable de commande. Le
système s'écrit, en première approximation,
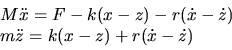 |
(1) |
Figure:
Simple masse reliée élastiquement à un
moteur linéaire.
|
On désire générer des déplacements arrêt-arrêt rapides de l'ensemble
masse-moteur pour positionner la masse de façon précise et par
conséquent sans oscillation. Notons que dès que la force 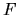 n'est
pas nulle, le moteur se déplace et, à cause de la tige flexible,
engendre une dynamique oscillante de la masse.
n'est
pas nulle, le moteur se déplace et, à cause de la tige flexible,
engendre une dynamique oscillante de la masse.
Dans ce qui suit, nous prenons 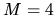 kg pour la masse du moteur,
kg pour la masse du moteur,
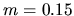 kg pour la masse transportée,
kg pour la masse transportée,
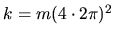 N/m
pour la raideur de la tige (qui correspond à une fréquence propre de
4 Hz),
N/m
pour la raideur de la tige (qui correspond à une fréquence propre de
4 Hz),
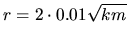 Ns/m pour le coefficient
d'amortissement de la tige (qui correspond à une constante de temps
d'amortissement de
Ns/m pour le coefficient
d'amortissement de la tige (qui correspond à une constante de temps
d'amortissement de
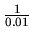 s).
s).
Dans un premier temps, on veut effectuer le
déplacement sans tenir compte de la masse transportée. Pour cela, on
fait comme si le système était donné par
les contributions de la masse transportée étant considérées comme des
perturbations.
Ainsi, pour un déplacement arrêt-arrêt partant de
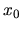 au repos à l'instant 0 et arrivant à
au repos à l'instant 0 et arrivant à 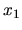 au repos à
l'instant
au repos à
l'instant 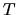 , avec la force et sa dérivée nulles aux instants 0 et
, avec la force et sa dérivée nulles aux instants 0 et
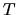 , on peut prendre comme trajectoire de référence
, on peut prendre comme trajectoire de référence
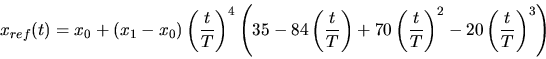 |
(2) |
On vérifie alors que la référence de la force 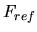 est donnée par
est donnée par
Pour rendre le déplacement du moteur insensible aux perturbations, on
ajoute à la force de référence une boucle PID :
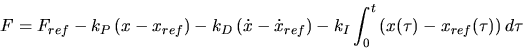 |
(3) |
Exécuter le fichier
Smasse0.sci.
Pour un déplacement de
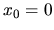 à
à
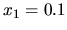 m, régler la durée
m, régler la durée 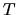 telle que le maximum du module de la force de référence ne dépasse pas
telle que le maximum du module de la force de référence ne dépasse pas
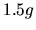 .
Régler les gains
.
Régler les gains 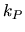 ,
, 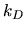 et
et 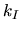 du PID
pour que l'influence de la masse transportée soit presque insensible
sur la position du moteur. Quelle amplitude d'oscillations
de la masse transportée obtient-on ?
Peut-on modifier la fréquence d'oscillation et la
constante de temps d'amortissement de la masse transportée ?
du PID
pour que l'influence de la masse transportée soit presque insensible
sur la position du moteur. Quelle amplitude d'oscillations
de la masse transportée obtient-on ?
Peut-on modifier la fréquence d'oscillation et la
constante de temps d'amortissement de la masse transportée ?
On veut essayer d'empêcher les oscillations de la masse sans
toutefois observer sa position. Pour cela, on va utiliser le
modèle (1) pour chercher des trajectoires de consigne de
déplacement du moteur et de la force telles que le moteur et la masse
transportée arrivent au point final au repos à l'instant 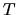 .
.
Exprimer 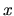 ,
, 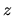 et
et 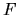 en fonction d'une sortie
plate du système (1) et de ses dérivées.
En déduire une trajectoire arrêt-arrêt pour le moteur
et la masse transportée partant de
en fonction d'une sortie
plate du système (1) et de ses dérivées.
En déduire une trajectoire arrêt-arrêt pour le moteur
et la masse transportée partant de 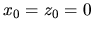 à l'instant
à l'instant 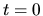 à
à
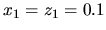 m à l'instant
m à l'instant 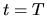 calculé précédemment.
Exécuter le fichier
Smasse1.sci. Régler les
gains
calculé précédemment.
Exécuter le fichier
Smasse1.sci. Régler les
gains 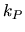 ,
, 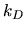 et
et 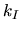 du PID, pour assurer la stabilité et
la robustesse d'erreur de
suivi dans le cas d'une erreur sur les conditions intiales de l'ordre
de 5% sur
du PID, pour assurer la stabilité et
la robustesse d'erreur de
suivi dans le cas d'une erreur sur les conditions intiales de l'ordre
de 5% sur 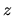 , ou sur les masses, raideurs et amortissements de
l'ordre de 0.01%.
En reprenant la méthode de la première partie, régler
la durée
, ou sur les masses, raideurs et amortissements de
l'ordre de 0.01%.
En reprenant la méthode de la première partie, régler
la durée 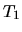 pour que la loi de commande (3) avec
(2), où
pour que la loi de commande (3) avec
(2), où 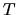 est remplacée par
est remplacée par 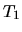 , produise des
oscillations de la masse transportée de même amplitude qu'aux
questions 2.2 et 2.3 avec
, produise des
oscillations de la masse transportée de même amplitude qu'aux
questions 2.2 et 2.3 avec 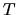 .
.
Reprendre l'étude précédente en ajoutant une seconde masse
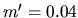 kg reliée au moteur par une seconde tige flexible dont les
caractéristiques sont
kg reliée au moteur par une seconde tige flexible dont les
caractéristiques sont
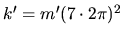 N/m (fréquence propre de
7 Hz) et
N/m (fréquence propre de
7 Hz) et
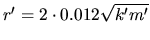 Ns/m (constante de temps
d'amortissement de
Ns/m (constante de temps
d'amortissement de
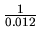 s). L'étude du déplacement du
moteur sans tenir compte des masses transportées se fait à l'aide du
fichier
Dmasses0.sci, et celle tenant compte des masses
transportées
à l'aide du fichier Dmasses1.sci. On pourra modifier
s). L'étude du déplacement du
moteur sans tenir compte des masses transportées se fait à l'aide du
fichier
Dmasses0.sci, et celle tenant compte des masses
transportées
à l'aide du fichier Dmasses1.sci. On pourra modifier  et les gains du PID en faisant exécuter les fichier Scilab.
et les gains du PID en faisant exécuter les fichier Scilab.
Figure:
Deux masses reliées élastiquement à un
moteur linéaire.
|
Dans ce cas, le système est donné par
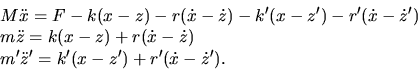 |
(4) |
On pourra se servir des formules
et, pour générer des trajectoires
arrêt-arrêt :



Jean-Philippe CHANCELIER
2002-04-24
![]() , se
déplaçant le long d'un rail rectiligne, relié à un corps de masse
, se
déplaçant le long d'un rail rectiligne, relié à un corps de masse
![]() par une tige flexible de masse négligeable que l'on
peut assimiler à un ensemble ressort-amortisseur, le ressort ayant une
raideur
par une tige flexible de masse négligeable que l'on
peut assimiler à un ensemble ressort-amortisseur, le ressort ayant une
raideur ![]() et l'amortisseur un coefficient d'amortissement
et l'amortisseur un coefficient d'amortissement ![]() .
L'abscisse du moteur (resp. de la masse) est notée
.
L'abscisse du moteur (resp. de la masse) est notée ![]() (resp.
(resp. ![]() ).
Le moteur produit une force
).
Le moteur produit une force ![]() qui est la variable de commande. Le
système s'écrit, en première approximation,
qui est la variable de commande. Le
système s'écrit, en première approximation,
![]() n'est
pas nulle, le moteur se déplace et, à cause de la tige flexible,
engendre une dynamique oscillante de la masse.
n'est
pas nulle, le moteur se déplace et, à cause de la tige flexible,
engendre une dynamique oscillante de la masse.
![]() kg pour la masse du moteur,
kg pour la masse du moteur,
![]() kg pour la masse transportée,
kg pour la masse transportée,
![]() N/m
pour la raideur de la tige (qui correspond à une fréquence propre de
4 Hz),
N/m
pour la raideur de la tige (qui correspond à une fréquence propre de
4 Hz),
![]() Ns/m pour le coefficient
d'amortissement de la tige (qui correspond à une constante de temps
d'amortissement de
Ns/m pour le coefficient
d'amortissement de la tige (qui correspond à une constante de temps
d'amortissement de
![]() s).
s).
![]() au repos à l'instant 0 et arrivant à
au repos à l'instant 0 et arrivant à ![]() au repos à
l'instant
au repos à
l'instant ![]() , avec la force et sa dérivée nulles aux instants 0 et
, avec la force et sa dérivée nulles aux instants 0 et
![]() , on peut prendre comme trajectoire de référence
, on peut prendre comme trajectoire de référence
![]() est donnée par
est donnée par