J.Ph. Chancelier1
On cherche ici à trouver numériquement
![]() tel que
tel que
![]() où
où ![]() est une fonction strictement
croissante donnée et
est une fonction strictement
croissante donnée et ![]() un réel donné.
On suppose par ailleurs que la fonction
un réel donné.
On suppose par ailleurs que la fonction ![]() est donnée par :
est donnée par :
Un algorithme stochastique pour trouver un zéro de
![]() sera le suivant. On se donne
sera le suivant. On se donne ![]() et une suite de variables
aléatoire
et une suite de variables
aléatoire
![]() indépendantes et de même loi que
indépendantes et de même loi que
![]() . On met à jour
. On met à jour ![]() l'estimation de
l'estimation de ![]() par :
par :
Écrire une fonction Scilab qui mets en oeuvre cet algorithme.
La fonction dont on cherche à calculer le zéro sera passée en
argument. Faire tourner l'algorithme sur une fonction de votre
choix (![]() , ou
, ou ![]() , ...).
, ...).
function y=dosage(x)
// on cherche un zéro de dosage(x) + un bruit gaussien
y= exp(x)
y= y + rand(1,1,'n');
endfunction
function x=rob_monro(x0,f,a,n,stop)
x= 0*ones(1,n);
x(1)=x0;
for i=2:n
x(i) = x(i-1) - (1/n)*( f(x(i-1)) -a )
if (abs(x(i)-x(i-1))) < stop*abs(x(i)) then
x(i+1:$)=[];
return
end
end
endfunction
n= 200000;
x=rob_monro(0,dosage,7,n,1.e-8) ;
nr=size(x,'*')
plot2d((1:nr)',x')
plot2d((1:nr)',log(7)*ones(nr,1))
On regarde dans cette section le cas particulier où on cherche à
évaluer un quantile. Soit ![]() la fonction de répartition
d'une loi
la fonction de répartition
d'une loi ![]() . On suppose ici
. On suppose ici ![]() continue.
Calculer un quantile d'ordre
continue.
Calculer un quantile d'ordre ![]() de
de ![]() consiste
à calculer
consiste
à calculer
![]() vérifiant :
vérifiant :
On peut donc utiliser l'algorithme décrit dans la section précédente.
une autre méthode est aussi envisageable. Soient
![]()
![]() tirages indépendants de loi
tirages indépendants de loi ![]() .
On peut les réordonner en ordre croissant
.
On peut les réordonner en ordre croissant
![]() et
estimer le quantile d'ordre
et
estimer le quantile d'ordre ![]() par
par ![]() avec
avec
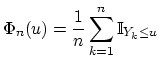
Mettre en oeuvre les deux algorithmes par exemple pour la loi normale
ou pour d'autres loi de votre choix (grand). Pour l'algorithme sur la
fonction de répartition empirique on pourra utiliser dsearch
pour rajouter un élément dans un tableau déjà trié.
Une estimation d'un quantile dans scilab
On estime le quantile a partir de la distribution empirique
a l'etape k xk contiendra le vecteur des xi tries
auquel on rajoute -l'utilisation de dsearch.
alpha = 0.5
xk=[-%inf,+%inf];
n=10000;
q=0*ones(1,n);
// En utilisant le quantile empirique
for i=1:n
xn = grand(1,1,'nor',0,1);
in=dsearch(xn,xk);
xk=[xk(1:in),xn,xk(in+1:i+1)];
// estimation du quantile
j=max(0,floor(alpha*i));
q(i)= xk(1+j); // On rajoute 1 a cause du -%inf
end
plot2d((1:n)',q);
// En utilisant un algorithme stochastique
// que l'on fait tourner par block
n=10000;
qrm(1)=1;
p= 0
function [qrm]=quantile_os(qrm,n,nb)
ns=1
while %t
qrm(1)=qrm($) ;
for i=2:n
xn = grand(1,1,'nor',0,1);
qrm(i)= qrm(i-1) - (1/(i+p))* ( sign(max(0,qrm(i-1) -xn)) -alpha );
end
xbasc();
plot2d((1:n)',qrm);
xclick();
ns = ns+1;
p= p+n;
if ns == nb then return ; end
end
endfunction
// on itere 10 fois par block de 1000 points avec
// un graphique tous les 1000 points
qrm=quantile_os(qrm,1000,10);
Faire une animation graphique montrant l'évolution des deux
algorithme aux cours des itérations. Pour certaines lois
donc la loi normale on peut calculer les quantiles dans Scilab
(cdfnor). On pourra utiliser cela pour superpose sur les
courbes la solution
![]() .
.
driver('X11')
xset('pixmap',1) // on utilise un mémoire graphique pour dessiner
for i=1:n
.......
xset('wwpc') // efface la mémoire graphique
// commande graphiques à introduire ici
xset('wshow') // affiche le contenu de la mémoire graphique à l'écran.
end
On suppose cette fois que l'on veut maximiser une fonction concave
![]() . On pourrait utiliser des méthodes
d'optimisation déjà vue, par exemple une méthode de gradient sur
la fonction
. On pourrait utiliser des méthodes
d'optimisation déjà vue, par exemple une méthode de gradient sur
la fonction ![]() mais cela demanderait à chaque itération
l'évaluation d'une espérance
mais cela demanderait à chaque itération
l'évaluation d'une espérance
![]() .
On va donc plutôt utiliser un algorithme stochastique pour trouver
un zéro de
.
On va donc plutôt utiliser un algorithme stochastique pour trouver
un zéro de
![]() et plutôt que de calculer
explicitement le gradient on va l'évaluer par :
et plutôt que de calculer
explicitement le gradient on va l'évaluer par :
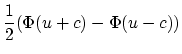
Mettre en oeuvre cet algorithme dans Scilab.
function z=f(x,y)
z= - x^2 + y
endfunction
function z=df(x,y)
z= -2*x
endfunction
function x=kiwolf(x0,f,n)
x= 0*ones(1,n);
x(1)=x0;
alpha=1/4;
for i=2:n
eps1= grand(1,1,'nor',0,1)
eps2= grand(1,1,'nor',0,1)
gn=(1/n)
cn=n^(-alpha)
x(i) = x(i-1) + (gn/cn)*(f(x(i-1)+cn,eps1) - f(x(i-1)-cn,eps2))
end
endfunction
function x=gstoch(x0,f,n)
x= 0*ones(1,n);
x(1)=x0;
alpha=1/4;
for i=2:n
eps1= grand(1,1,'nor',0,1)
gn=(1/n)
cn=n^(-alpha)
x(i) = x(i-1) + (gn/cn)*( df(x(i-1),eps1))
end
endfunction
n= 2000;
x= kiwolf(1,f,n) ;
y= gstoch(1,f,n) ;
plot2d((1:n)',x')
On se propose d'implémenter en Scilab un simulateur de
trajectoire d'un mouvement brownien sur
![]() .
On pourra se reporter sur les pages du cours
cours (p39)
pour retrouver la méthodologie proposée.
Il est proposé dans le polycopié une implémentation récursive par
contre dans Scilab on utilisera une implémentation itérative.
.
On pourra se reporter sur les pages du cours
cours (p39)
pour retrouver la méthodologie proposée.
Il est proposé dans le polycopié une implémentation récursive par
contre dans Scilab on utilisera une implémentation itérative.
k de l'algorithme de la valeur
du Brownien que l'on a simulé aux date tk.
k1+ on decoupe chaque intervalle de temps en
// construction du brownien sur [0,1] vk=[ 0, grand(1,1,'nor',0,1)]; tk=[ 0, 1]; dk= 1; nk = 1; // On rajoute des points entre chaque points de tk n=20; eq=0*ones(1,n); for i=1:10 // nkp1 = 2*nk; dkp1 = dk/2; vkp1 = ones(1,nkp1+1); tkp1 = ones(1,nkp1+1); vkp1(1:2:$) = vk; vkp1(2:2:$) = ( vk(1:$-1)+vk(2:$))/2 + grand(1,nk,'nor',0,1)*(1/2)*sqrt(dk); eqk= vkp1(2:$)-vkp1(1:$-1); eq(i) = norm(eqk)^2; tkp1(1:2:$) = tk; tkp1(2:2:$) = ( tk(1:$-1)+tk(2:$))/2 ; xbasc(); plot2d(tk,vk) xclick(); nk=nkp1; tk=tkp1; dk=dkp1; vk=vkp1; tk=tkp1; end