Décomposition de domaine

J.Ph. Chancelier1

Version pdf de ce document

1 Décomposition de domaine

1.1 conditions de Dirichlet et recouvrement

On cherche ici à mettre en \oeuvre la méthode de décomposition de domaine décrite dans la partie Calcul scientifique du cours Mopsi. On cherche à résoudre une équation de laplace en dimension 1.

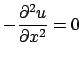
$\displaystyle -\frac{\partial^2 u}{\partial x^2} = 0 $

où $ u$ est une fonction scalaire de la variable d'espace $ x\in [a,b]$ avec les conditions aux limites :

$\displaystyle u(a)= u_a$   et$\displaystyle \quad u(b) = u_b $

Écrire tout d'abord une fonction qui résout par une méthode de différences finies le problème de Dirichlet précédent. N désigne le nombre de points de discrétisation à utiliser. La fonction doit renvoyer deux vecteurs de taille N, u et x et le pas de discrétisation h. u(i) est la solution calculée au point x(i) avec x(1)=a et x(N)=b. 

function [u,x,h]=diri(a,ua,b,ub,N)

Cette fonction peut être utilisée maintenant pour résoudre le problème général (on sait bien sur résoudre le problème à la main dans ce cas simpe 1-D) mais aussi résoudre les problèmes sur les sous domaines.

Supposons ici que $ (a,b)$ soit discrétisé en $ 2*N+1$ points. et soit $ h$ le pas de discrétisation. Les points de discrétisation sont donnés par xx=linspace(a,b,2*N1)+. On décompose le domaine $ (a,b)$ en $ (a,xp)$ et $ (xm,b)$ avec un recouvrement. Soit $ c=(a+b)/2= xx(N+1)$ on utilisera $ xp=xx(N+1+p)$ et $ xm=xx(N+1-p)$.

Programmer l'algorithme itératif de résolution par décomposition de domaine avec recouvrement dans sa version parallèle. Soit $ u_i^k$ les solutions sur chaque domaines à l'itération $ k$, on calcule $ u_i^{k+1}$ par


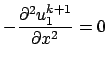$\displaystyle -\frac{\partial^2 u_1^{k+1}}{\partial x^2} = 0$   sur$\displaystyle \quad (a,xp)$     (1)
$\displaystyle u_1^{k+1}(a)= u_a$   et$\displaystyle \quad u_1^{k+1}(xp) = u_2^{k}(xp)$     (2)


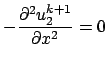$\displaystyle -\frac{\partial^2 u_2^{k+1}}{\partial x^2} = 0$   sur$\displaystyle \quad (xm,b)$     (3)
$\displaystyle u_2^{k+1}(xm)= u_1^{k}(xm)$   et$\displaystyle \quad u_2^{k+1}(b) = u_b$     (4)

On choisira le nombre de points de discrétisation de chaque sous problème de façon à ce que les points de discrétisation coincident avec les points $ xx$.

On dessinera au cours des itérations les solutions $ u_1^k$ et $ u_2^k$ et on calculera la norme de l'erreur que l'on tracera aussi en fonction des itérations.

On regardera par simulation l'influence de $ p$ qui contrôle l'a longueur de la zone de recouvrement.

1.2 conditions de Dirichlet et Neumann sans recouvrement

On utilise cette fois une condition de Dirichlet pour le calcul de $ u_1^k$ :


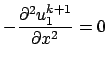$\displaystyle -\frac{\partial^2 u_1^{k+1}}{\partial x^2} = 0$   sur$\displaystyle \quad (a,c)$     (5)
$\displaystyle u_1^{k+1}(a)= u_a$   et$\displaystyle \quad u_1^{k+1}(c) = \gamma_k$     (6)

et une condition de Neumann pour le calcul de $ u_2^k$ :


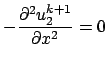$\displaystyle -\frac{\partial^2 u_2^{k+1}}{\partial x^2} = 0$   sur$\displaystyle \quad (c,b)$     (7)
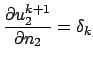$\displaystyle \frac{\partial u_2^{k+1}}{\partial n_2} = \delta_k$   et$\displaystyle \quad u_1^{k+1}(b) = u_b$     (8)

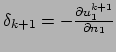$ \delta_k$ et $ \gamma_k$ étant remis à jours par $ \delta_{k+1} = - \frac{\partial u_1^{k+1}}{\partial n_1}$ et $ \gamma_{k+1} = \theta u_2^{k+1}+(1-\theta)\gamma_k$ ;

On choisira ici $ (a,b)=(-1,1)$ et $ c=0$, on que cet algorithme converge pour $ \theta$ tel que :

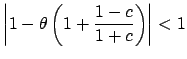
$\displaystyle \left\vert 1- \theta \left(1+ \frac{1-c}{1+c}\right)\right\vert < 1 $

1.3 Utilisation de pvm

On cherche ici à utiliser pvm pour paralléliser la résolution par décomposition de domaine.

Un programme principal decomp-master.sce est utilisé pour lancer deux programmes Scilab esclaves. Chaque esclave est responsable du calcul sur l'un des sous domaines et communique à chaque itération la valeur qui sera utilisée comme condition de Dirichlet par l'autre esclave

On donne ici le code Scilab du programme maître, le code du programme esclave restant à écrire decomp-slave.sce. 

ok=pvm_start()  // je démarre pvm 
if ok<>0 then disp('pvm daemon already active'),end;

N=2; // je lance 2 nouveau scilab 
path=get_absolute_file_path('decomp-master.sce');
[task_id,numt] = pvm_spawn(path+'/decomp-slave.sce',N)
if numt<0 then disp(['pvm_spawn aborts to create a new process']); end 

// nombre d'itérations 
n_step = 50; 

// envois du nombre d'itérations 
// et du numero du sous domaine ŕ résoudre 
for i=1:2
  pvm_send(task_id(i),[i,n_step],0);
end 

// itération avec échange des conditions de dirichlet 
for k=1:n_step 
  bb1= pvm_recv(task_id(1),0);
  bb2= pvm_recv(task_id(2),0);
  pvm_send(task_id(1),bb2,0);
  pvm_send(task_id(2),bb1,0);
end

// les solutions sur chaque domaine 
u1=pvm_recv(task_id(1),0);
x1=pvm_recv(task_id(1),0);

u2=pvm_recv(task_id(2),0);
x2=pvm_recv(task_id(2),0);

// un graphique 
plot2d(x1,u1);
plot2d(x2,u2);

x_message(['Job finished'])
pvm_halt()


Notes

... Chancelier1
Cermics, École Nationale des Ponts et Chaussées, 6 et 8 avenue Blaise Pascal, 77455, Marne la Vallée, Cedex 2