




Next: Équations de complexité
Up: No Title
Previous: La fonction main (2)
Un algorithme diviser pour régner a la structure suivante : pour
résoudre un problème de taille n, l'algorithme consiste à décomposer
le problème en a sous-problèmes ayant tous la taille n/b (peut-être
approximativement), à appliquer l'algorithme à ces sous-problèmes, puis
à construire une solution du problème en composant les solutions des
sous-problèmes. Non seulement cette méthode est naturelle , mais
elle permet souvent une réduction importante de la complexité T(n).
Voici quelques exemples :
, mais
elle permet souvent une réduction importante de la complexité T(n).
Voici quelques exemples :
-
recherche dichotomique dans une table ordonnée (a=1, b=2) :
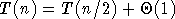 , d'où
, d'où 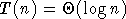 , alors qu'une
recherche séquentielle dans une table ordonnée est en
, alors qu'une
recherche séquentielle dans une table ordonnée est en 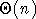
-
tri d'une table par fusion (a=2, b=2) :
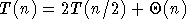 , d'où
, d'où 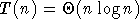 , alors qu'un
tri ordinaire est typiquement en
, alors qu'un
tri ordinaire est typiquement en 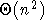
-
transformée de Fourier rapide (a=2, b=2) :
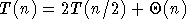 , d'où
, d'où 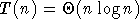 , alors qu'une
évaluation directe des formules est en
, alors qu'une
évaluation directe des formules est en 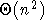
- multiplication de deux matrices par l'algorithme de Strassen
(a=7, b=2) :
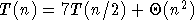 , d'où
, d'où 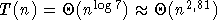 alors que la multiplication
ordinaire est en
alors que la multiplication
ordinaire est en 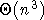
Rene Lalement
Mon Sep 30 18:22:54 MET 1996
![]() , mais
elle permet souvent une réduction importante de la complexité T(n).
Voici quelques exemples :
, mais
elle permet souvent une réduction importante de la complexité T(n).
Voici quelques exemples :