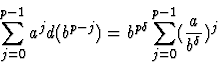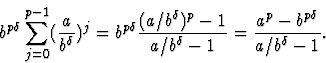Next: La transformée de Fourier
Up: No Title
Previous: Diviser pour régner
Soit T(n) la complexité dans le pire des cas de l'algorithme appliqué
à un problème de taille n. On suppose que la complexité des opérations
de décomposition du problème et de recomposition des solutions des
sous-problèmes a une complexité en d(n). Enfin, on se donne la
complexité T(1) sur un problème de taille 1. La complexité de
l'algorithme est donc déterminée par l'équation de récurrence suivante :
T(n) = aT(n/b) + d(n)
Résolvons ces équations quand n est une puissance de b ; dans ce cas
l'équation s'écrit :
T(bp) = a T(bp-1) + d(bp)
Sa solution est
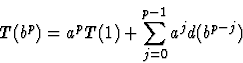
Le premier terme, 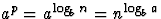 correspond à la
complexité due à la résolution de tous les sous-problèmes ; le second
terme est la complexité due à toutes les opérations de
décomposition/recomposition.
correspond à la
complexité due à la résolution de tous les sous-problèmes ; le second
terme est la complexité due à toutes les opérations de
décomposition/recomposition.
Examinons ce deuxième terme quand 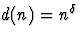 . On a
. On a
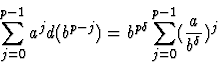
Discutons selon les valeurs relatives de a et 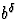 .
.
- Si
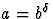 , cette somme vaut
, cette somme vaut 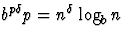 ;
donc
;
donc 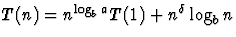 . Ainsi, si
. Ainsi, si 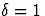 et a=b (cas très usuel, en particulier de la FFT, du tri par fusion
et du tri rapide), on a
et a=b (cas très usuel, en particulier de la FFT, du tri par fusion
et du tri rapide), on a 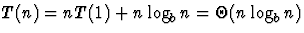 . Si
. Si 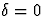 et a=1 (cas de la recherche dichotomique), on
obtient
et a=1 (cas de la recherche dichotomique), on
obtient 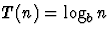 .
. -
Si
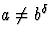 ,
,
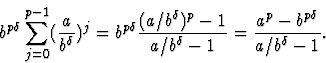
- Si
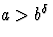 , le terme dominant est
, le terme dominant est 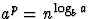 , qui
est indépendant de
, qui
est indépendant de 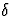 et qui est du même ordre que le premier
terme, donc
et qui est du même ordre que le premier
terme, donc 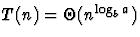 . Ainsi, si
. Ainsi, si 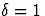 et
a>b (cas de la multiplication matricielle de Strassen, où
a=7 et b=2), on a
et
a>b (cas de la multiplication matricielle de Strassen, où
a=7 et b=2), on a 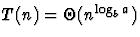 .
. -
Si
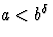 , le terme dominant est
, le terme dominant est 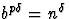 , donc
, donc
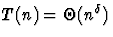 . La décomposition du problème ne conduit
dans ce dernier cas à aucune accélération, les opérations de
décomposition et recomposition étant dominantes. C'est le cas de
l'équation T(n) = 2T(n/2) + n2.
. La décomposition du problème ne conduit
dans ce dernier cas à aucune accélération, les opérations de
décomposition et recomposition étant dominantes. C'est le cas de
l'équation T(n) = 2T(n/2) + n2.





Next: La transformée de Fourier
Up: No Title
Previous: Diviser pour régner
Jean-Philippe Chancelier
9/29/1998
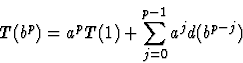
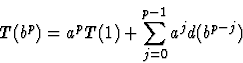
![]() . On a
. On a