Décision dans l'incertain
¶

Un exemple simple de problème de décision
¶

$\newcommand\indi[1]{{\mathbf 1}_{\displaystyle #1}}$ $\newcommand\inde[1]{{\mathbf 1}_{\displaystyle\left\{ #1 \right\}}}$ $\newcommand{\ind}{\inde}$ $\newcommand\E{{\mathbf E}}$ $\newcommand\Cov{{\mathrm Cov}}$ $\newcommand\Var{{\mathrm Var}}$

1. La question à résoudre¶

On place deux oeufs "au hasard" dans une matrice $p\times q$. On considère deux joueurs ($A$ et $B$). Le joueur $A$ parcours la matrice en colonne, le joueur $B$ en ligne. Le gagnant est celui qui atteint le premier l'un des deux oeufs. La question est de savoir si ce jeu est équitable (i.e. les deux joueurs ont ils la même probabilité de gagner ?) et de déterminer, si ce n'est pas le cas, lequel a un avantage.

On trouvera la réponse à cette question lorsque $p=3$ et $q=4$ sur le site de la NSA. Nous verrons que l'on peut répondre très simplement à ces questions à l'aide d'un programme de quelques lignes pour une valeur arbitraire de $p$ et $q$.

Les réponses dépendent des valeurs de $p$ et $q$ de façon surprenante: elles sont différentes pour $(p=3,q=4)$, $(p=4,q=4)$ et $(p=4,q=5)$!

Remarque:
Lorsque vous aurez terminé la partie informatique, les parties en bleu pourront vous servir d'exercices (de révision du cours du premier semestre).

2. Étude de la question posée par une méthode de Monte-Carlo¶

On commence par traiter la question par simulation.

On suppose (ce qui est implicite dans la formulation du problème) que les $2$ oeufs sont placés, indépendamment, uniformément sur les $p\times q$ cases de la matrice. Il peut donc arriver que les $2$ oeufs soient au même endroit (à vrai dire le problème ne précise pas ce détail), mais cela n'a pas d'importance pour la réponse à la question posée.

On doit tirer une ligne au hasard uniformement entre $1$ et $p$ et une colonne au hasard entre $1$ et $q$. Pour cela il faut savoir tirer au hazard une variable aléatoire selon une loi discrête donnée. C'est l'objet de la question 1.

Dans la question 2, on tire au hazard les 2 oeufs et on en déduit les temps d'atteinte par A et B du premier oeuf (notés respectivement $T_A$ et $T_B$).

Dans la question 3, on répond à la question "qui gagne le plus souvent?" en simulant un grand nombre de parties (une méthode de Monte-Carlo).

Simulation d'une loi discrète¶

Rappel:

Il est possible de simuler une variable aléatoire qui prend les valeurs $(x_i)_{i\in \mathbb{N}^*}$ avec probabilités respectives $(p_i)_{i \in \mathbb{N}^*}$ (avec les $p_i \geq 0$ et $\sum\limits_{i \in \mathbb{N}^*} p_i = 1$) à l'aide d'une seule variable aléatoire $U \sim \mathcal{U}([0, 1])$ en posant:

$$ X = x_1 \mathbb{1}_{ \{U \leq p_1 \} } + x_2 \mathbb{1}_{ \{p_1 \leq U \leq p_1 + p_2 \}} + \dots + x_i \mathbb{1}_{ \{p_1 + \dots + p_{i-1} \leq U \leq p_1 + \dots + p_i \}} + \dots $$

On cherche à réaliser un tirage selon la loi d'une variable aléatoire $N$ qui prend ses valeurs dans $\{1,\ldots,n\}$ dont la loi donnée par le vecteur $(P[k-1],1\leq k \leq n)$.

Exercice 1:
Lorsque la loi est uniforme sur $\{1,\ldots,n\}$, on peut vérifier (exercice) que $\E(N)=\frac{n+1}{2}$ et $\Var(N)=\frac{(n+1)(n-1)}{12}$.

In [1]:
import random
import numpy as np
import math

def rand_disc(P):
# P est une loi discrète qui charge les entiers 1,...,p
# le vecteur P[i-1],pour i=1,...,p donne la probabilité d'obtenir i .
# Il est décalé de 1 pour tenir compte de la convention "Python"
# de vecteurs qui débutent en 0.

# Version itérative.
    U=np.random.rand(1) # On tire selon une loi uniforme entre 0 et 1
    # "On inverse la fonction de répartition" : voir cours du premier semestre.

    ######  A vous de jouer  .....
In [2]:
n=12
P=np.ones(n)/n
X=np.zeros(1000,dtype=int) # dtype=int pour indiquer que le tableau est constitué d'entiers
for i in range(1000):
    X[i]=rand_disc(P)
print("moyenne empirique:",np.mean(X)," - moyenne attendue ",(n+1)/2) # np.mean calcule moyenne des tirages
print("variance:",np.var(X)," - variance attendue ",(n+1)*(n-1)/12) # np.var la variance des tirages

moyenne empirique: 6.606  - moyenne attendue  6.5
variance: 11.632764  - variance attendue  11.916666666666666
In [3]:
def test_0():
# Un exemple de tirages uniformes sur |$\{1,2,3\}$|
    p=3;
    P=np.ones(p)/p;# loi uniforme sur |$\{1,2,3\}$|

    N=10;
    X=np.zeros(N,dtype=int)
    for i in range(N): # N tirages uniformes sur |$\{1,2,3\}$|
        X[i] = rand_disc(P)
        print(X[i], end=' ')
        
test_0()

2 2 2 3 3 1 2 3 3 3

Simulation des temps d'atteinte¶

On tire le premier oeuf en $(U_1,V_1)$, $U_1$ (l'indice de ligne) et $V_1$ (l'indice de colonne) étant indépendantes, de loi uniforme respectivement sur $\{1,\ldots,p\}$ et $\{1,\ldots,q\}$. Si le premier oeuf se trouve en $(U_1,V_1)$, le temps d'atteinte de cet oeuf par $A$ (parcours en colonne) est donné par $$ t_1^A=(V_1-1) p+U_1, $$

et, pour $B$ (parcours en ligne), par $$ t_1^B=(U_1-1) q+V_1, $$

avec des formules identiques pour le deuxième oeuf: $$ t_2^A=(V_2-1) p+U_2,\quad t_2^B=(U_2-1) q+V_2, $$ $U_2$ et $V_2$ étant indépendantes, toujours de lois uniformes, indépendantes du couple $(U_1,V_1)$.

Exercice 2:
Noter que l'on peut calculer la loi (commune) de $t_1^A$, $t_1^B$, $t_2^A$, $t_2^B$ (loi uniforme sur $\{1,\ldots,p\times q\}$) et montrer que $t_1^A$ s'obtient comme une permutation déterministe $\sigma$ de $t_1^B$.

Avec ces éléments, il est facile d'écrire une fonction qui réalise le tirage des deux oeufs dans la matrice et d'en déduire les temps que mettent $A$ et $B$ pour trouver le premier oeuf (au sens chronologique).

En d'autres termes:

$$ T_A = \min(t_1^A, t_2^A), \quad T_B = \min(t_1^B, t_2^B) $$

Exercice 3:
Montrer que $T_A$ et $T_B$ ont la même loi et que si $\sigma^2 = id$ alors les couples $(T_A, T_B)$ et $(T_B, T_A)$ ont la même loi (c'est le cas lorsque $p=q$).

In [4]:
def random_times(p,q):
# On simule selon des lois uniformes sur 1:p et 1:q
# On en déduit les tirages de T_A et T_B

    P=np.ones(p)/p;# Loi uniforme sur 1:p
    Q=np.ones(q)/q;# Loi uniforme sur 1:q

    # Calcul de T_A et T_B en fonction de (i_1,j_1) (i_2,j_2)
    
    
    ######  A vous de jouer  .....
    
    
    return [T_A,T_B]
In [5]:
random_times(2,3)
Out[5]:
[1, 1]

Il ne reste plus qu'à faire suffisamment de tirages pour répondre (en partie) à la question posée.

In [6]:
def qui_gagne_MC(p,q,N):
    print("*"*70)
    print("Pour p = {}, q = {}:".format(p, q))
    statA = 0 
    statB = 0
    # Nombre de fois où chaque joueur gagne
    
        ######  A vous de jouer  .....
    for i in range(N):
        [T_A,T_B] = random_times(p,q);

        ### Comment estimer par simulation pA=P(A gagne) et pB=P(B gagne) ?
    

    erreur=1/math.sqrt(N) # erreur maximum probable
       
    print("pA = {:.3f} +- {:.3f}, pB = {:.3f} +- {:.3f}".format(pA, erreur, pB, erreur))

    if (pA+erreur < pB-erreur):
        print("Il est très probable que B gagne en moyenne.")

    elif (pA-erreur > pB+erreur):
        print("Il est très probable que A gagne en moyenne.")

    else:
        print("On ne peut pas conclure (il faut augmenter le nombre de tirages)")


def test_1():
    N=10000;
    qui_gagne_MC(2,3,N)
    qui_gagne_MC(3,4,N)
    qui_gagne_MC(4,5,N)
    qui_gagne_MC(4,4,N)

test_1()

**********************************************************************
Pour p = 2, q = 3:
pA = 0.279 +- 0.010, pB = 0.330 +- 0.010
Il est très probable que B gagne en moyenne.
**********************************************************************
Pour p = 3, q = 4:
pA = 0.394 +- 0.010, pB = 0.413 +- 0.010
On ne peut pas conclure (il faut augmenter le nombre de tirages)
**********************************************************************
Pour p = 4, q = 5:
pA = 0.438 +- 0.010, pB = 0.440 +- 0.010
On ne peut pas conclure (il faut augmenter le nombre de tirages)
**********************************************************************
Pour p = 4, q = 4:
pA = 0.365 +- 0.010, pB = 0.364 +- 0.010
On ne peut pas conclure (il faut augmenter le nombre de tirages)

Exercice 4:
Noter que le théorème de la limite centrale permet (exercice!) de montrer que l'erreur "probable maximale" est de l'ordre de $1/\sqrt{n}$ (C'est le même résultat qui permet d'évaluer approximativement l'erreur d'un sondage d'opinion).

Dans le cas $p=2$, $q=3$ on arrive assez facilement ($N=10000$ suffit largement) à se convaincre que $B$ gagne en moyenne. C'est plus difficile pour $(p=3,q=4)$ ($N=100000$ convient). Ça devient délicat pour $(p=4,q=5)$ (il faut prendre $N\approx 1000000$ pour conclure que c'est $A$ qui gagne). Dans les cas où $p=q$ (où l'on peut prouver qu'il y a égalité des probabilités), une méthode de simulation ne sera jamais concluante.

Il nous faut une méthode exacte de calcul de ces probabilités. C'est ce que nous allons faire maintenant.

3. Un calcul exact par énumération exhaustive¶

L'espace de probabilité $\Omega$ étant fini, il suffit d'énumérer $\Omega$ pour calculer la probabilité: on génère toutes les valeurs possibles pour les positions des oeufs $(i_1,j_1)$ et $(i_2,j_2)$ (tous ces couples (de couples!) sont supposés équiprobables), on calcule $T_A$ et $T_B$ et l'on fait des stats sur celui qui gagne.


On en profite pour calculer la loi du couple $(T_A,T_B)$ et pour vérifier que les lois de $T_A$ et $T_B$ sont identiques (exercice, pour une correction voir la version scilab du sujet).

On vérifie aussi que la loi de $(T_A,T_B)$ n'est pas identique à celle de $(T_B,T_A)$ (sauf si $p=q$). On peut aussi montrer (exercice) que $T_A$ n'est jamais indépendante de $T_B$. </span>

In [7]:
def qui_gagne_elem(p,q):
# On énumère toutes les positions possibles
# et on en déduit lequel des joueurs gagne en moyenne

    Ascore=0;Bscore=0;nbre_cas_egalite=0
 
    # On génère toutes les positions pour les 2 oeufs
    # Attention en Python: range(1,p+1) = {1,2, ...,p}, c'est bien ce que l'on veut
                    
                    ######  A vous de jouer  .....
                    
                    if T_A > T_B :
                        Bscore=Bscore+1
                    elif T_A < T_B:
                        Ascore=Ascore+1
                    else: # T_A == T_B
                        nbre_cas_egalite=nbre_cas_egalite+1

    print('p = ',p,', q = ',q, ': ',end='') # end='' pour eviter le passage à la ligne
    if (Bscore>Ascore): 
      print("c'est B qui gagne")
    elif (Ascore>Bscore): 
      print("c'est A qui gagne")
    else: 
      print("cas d'égalité")

def histo(p,q):
# Calcule la loi du couple (T_A,T_B) par énumération exhaustive des cas

    nbre=p*q;# valeur maximale de T_A ou T_B
    
    # Les tableaux Python sont indicés à partir de 0 -> on rajoute 1
    H_AB=np.zeros([nbre+1,nbre+1]);
    
    # On génère toutes les positions pour les 2 oeufs 
                    
                    ######  A vous de jouer  .....
                    
                    
                    # met à jour le nbre de tirages valant (k,l)
                    H_AB[T_A,T_B] = H_AB[T_A,T_B] + 1
    H_AB = H_AB/(nbre*nbre) 
    return H_AB

p=40;q=45
qui_gagne_elem(p,q)

# On calcule la loi du couple (T_A,T_B)
H_AB=histo(p,q)

# On vérifie que H_AB est bien la loi d'un couple
if np.abs(np.sum(H_AB)-1) <= 1.e-7 :
    print('H_AB est bien de somme 1')

# Verification que les lois marginales sont identiques.

######  A vous de jouer  .....

# Vous pourrez utiliser np.linalg.norm(matrice)
# qui calcule la norme quadratique d'une matrice.

# np.sum(matrice,axis=0) fait la somme des lignes d'une matrice
# np.sum(matrice,axis=1) fait la somme des colonnes d'une matrice

#H_A=...
#H_B=...

# H_A = la loi de T_A est forcément égal à H_B = la loi de T_B : on va vérifier

     ######  A vous de jouer  .....

     #if ... : # H_A ?=? H_B à epsilon près ...
     #    print("Warning: les lois de T_A et T_B doivent être égales.\n")
     #else:
     #    print('Les lois de T_A et T_B sont bien égales.');

# Par contre (T_A,T_B) n'a pas la même loi que (T_B,T_A) lorsque p != q.
# La loi n'est pas symétrique (en particulier T_A et T_B ne peuvent être indépendantes)

# On va vérifier ce point.

    ######  A vous de jouer  .....

    # La loi (T_B,T_A) est donnée par la transposée de la loi de (T_A,T_B)
    # Il faut donc comparer la matrice H_AB et sa transposée.
    # En python pour transposer une matrice : np.transpose(matrice)

    # if np.linalg.norm(...) >= 1.e-7 :
    print("La loi du couple (T_A,T_B) n'est pas symétrique (c'est normal si p!=q) !\n")
else:
    print('La loi du couple (T_A,T_B) est symétrique: p et q sont probablement égaux.');

if p*q <=10:
    print(H_AB[1:p*q+1,1:p*q+1])

p =  40 , q =  45 : c'est A qui gagne
H_AB est bien de somme 1
Les lois de T_A et T_B sont bien égales.
La loi du couple (T_A,T_B) n'est pas symétrique (c'est normal si p!=q) !
In [8]:
def test_2():
    qui_gagne_elem(3,4);
    qui_gagne_elem(4,4);
    qui_gagne_elem(4,5);
  
    #for p in range(2,5): qui_gagne_elem(p,p+1)
    #for p in range(2,9): qui_gagne_elem(p,p+2)
    #for p in range(2,7): qui_gagne_elem(p,p+3)

test_2()

p =  3 , q =  4 : c'est B qui gagne
p =  4 , q =  4 : cas d'égalité
p =  4 , q =  5 : c'est A qui gagne

On retrouve le résultat, un peu surprennant, annoncé au début.

Références¶

Cours probabilités et statistique pour l'ingénieur - Benjamin Jourdain

Corrigés des exercices¶

Exercice 1:
Lorsque la loi est uniforme sur $\{1,\ldots,n\}$, on peut vérifier (exercice) que $\E(N)=\frac{n+1}{2}$ et $\Var(N)=\frac{(n+1)(n-1)}{12}$.

Solution:

Soit $N \sim \mathcal{U}(\{1, \dots, n\})$

On a: $$ \begin{align} \mathbb{E}[N] &= \sum\limits_{k=1}^{n} k \underbrace{\mathbb{P}(N = k)}_{=\frac{1}{n}} \\ &= \frac{1}{n} \sum\limits_{k=1}^{n} k \\ &= \frac{1}{n} \frac{n(n+1)}{2} \\ &= \frac{n+1}{2} \end{align} $$

$$ \begin{align} \mathbb{E}[N^2] &= \sum\limits_{k=1}^{n} k^2 \underbrace{\mathbb{P}(N = k)}_{=\frac{1}{n}} \\ &= \frac{1}{n} \sum\limits_{k=1}^{n} k^2 \\ &= \frac{1}{n} \frac{n(n+1)(2n+1)}{6} \\ &= \frac{(n+1)(2n+1)}{6} \end{align} $$

On en déduit que: $$ \begin{align} \mathbb{V}\text{ar}[N] &= \mathbb{E}[N^2] - \mathbb{E}[N]^2 \\ &= \frac{(n+1)(2n+1)}{6} - \left( \frac{n+1}{2} \right)^2 \\ &= \frac{(n+1)(n-1)}{12} \end{align} $$

Exercice 2:
Noter que l'on peut calculer la loi (commune) de $t_1^A$, $t_1^B$, $t_2^A$, $t_2^B$ (loi uniforme sur $\{1,\ldots,p\times q\}$) et montrer que $t_1^A$ s'obtient comme une permutation déterministe $\sigma$ de $t_1^B$.

Solution:

Les temps aléatoires $t_1^A$ et $t_1^B$ suivent tous les deux une loi uniforme sur $\{1,\ldots,p\times q\}$.

En effet, si $k$ est un nombre entier compris entre $0$ et $p\times q-1$, il s'écrit de façon unique sous la forme $k=i_1\times p + j_1$ avec $i_1\in\{0,1,\ldots,q-1\}$ et $j_1\in\{0,1,\ldots,p-1\}$.

On a donc:

$$ \mathbb{P}(t_1^A=k+1) = \mathbb{P}(V_1=i_1+1,U_1=j_1+1) = \mathbb{P}(V_1=i_1+1)\mathbb{P}(U_1=j_1+1) = 1/(p\times q). $$

Ces temps ne sont pas indépendants. En fait, $t_1^B$ s'obtient par une permutation déterministe à partir de $t_1^A$: il existe une permutation $\sigma$ de $\{1,\ldots,p\;q\}$ telle que $t_1^B=\sigma(t_1^A).$

Il est facile de s'en convaincre, puisque à chaque case $(i,j)$ correspond un temps d'atteinte différent pour chacun des joueurs: pour construite la permutation, il suffit donc de mettre en relation le temps mis par $A$ pour atteindre $(i,j)$ avec le temps mis par $B$ pour atteindre la même case.

On peut aussi voir que, lorsque l'on considère le jeu avec un seul oeuf, on a toujours un problème équitable (i.e. on a $\mathbb{P}(t_1^A < t_1^B) =\mathbb{P}(t_1^B < t_1^A)$).

Pour s'en convaincre, on écrit:

$$ \mathbb{P}(t_1^A<t_1^B) = \mathbb{P}(U'_1 p + V'_1 + 1 < V'_1 q + U'_1 + 1) = \mathbb{P}(U'_1 (p -1) < V'_1 (q-1)), $$

où $U'_1=U_1-1$ suit une loi uniforme sur $\{0,\ldots,q-1\}$ et $V'_1=V_1-1$ suit une loi uniforme sur $\{0,\ldots,p-1\}$, les deux étant indépendants.

Comme $(U'_1,V'_1)$ suit la même loi que $(q-1-U'_1,p-1-V'_1)$, on a:

$$ \begin{align*} \mathbb{P}(t_1^A<t_1^B) &= \mathbb{P}( (q-1-U'_1) (p-1) < (p-1-V'_1)(q-1) )\\ &= \mathbb{P}( U'_1 (p-1) > V'_1 (q-1) )\\ &= \mathbb{P}(t_1^B<t_1^A). \end{align*} $$

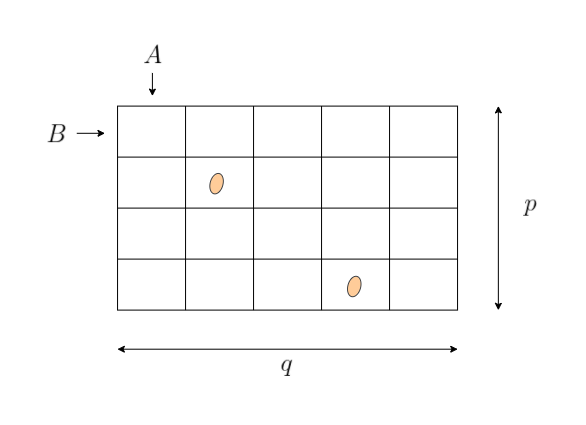
Exercice 3:
Montrer que $T_A$ et $T_B$ ont la même loi et que si $\sigma^2 = id$ alors les couples $(T_A, T_B)$ et $(T_B, T_A)$ ont la même loi.

Solution:

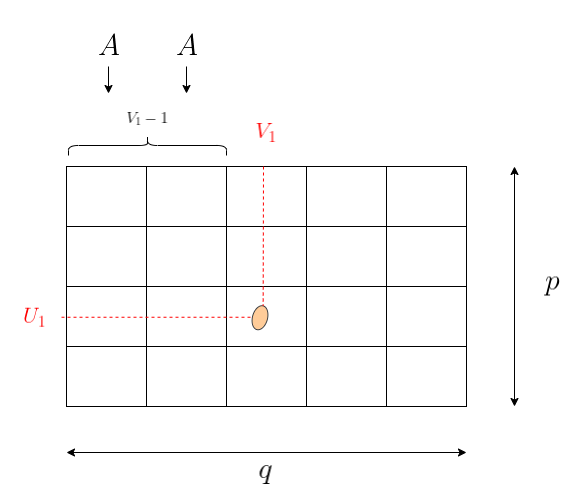
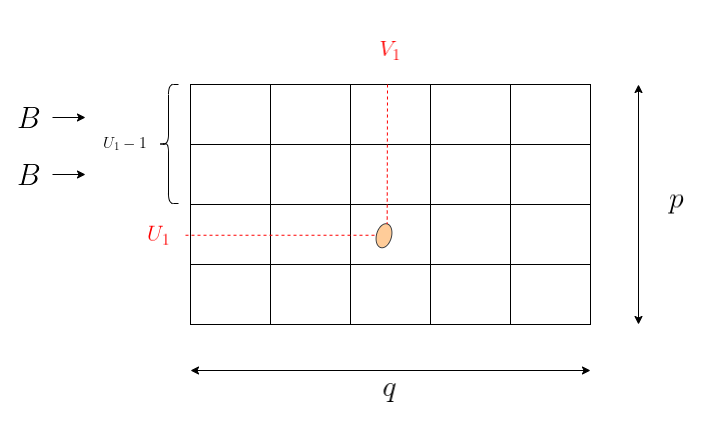
Pour montrer que $T_A$ et $T_B$ suivent la même loi, on commence par remarquer qu'il existe une permutation $\sigma$ de $\{1,\ldots,p\times q\}$ telle que $t^1_B=\sigma(t^1_A)$ et $t^2_B=\sigma(t^2_A)$ (elle est calculée plus tard, mais c'est facile de s'en convaincre).

Comme $t^1_A$ et $t^2_A$ suivent des lois uniformes sur $\{1,\ldots,p \times q\}$, c'est aussi le cas de $t^1_B$ et $t^2_B$ (exercice).

$t^1_B$ et $t^2_B$ sont indépendantes, puisque fonctions de variables aléatoires indépendantes.

Les couples $(t^1_A,t^2_A)$ et $(t^1_B,t^2_B)$ suivent donc la même loi et l'on conclut que $T_A$ et $T_B$ ont même loi puisque:

$$ T_A=\min(t^1_A,t^2_A),\quad T_B=\min(t^1_B,t^2_B). $$

Il convient de noter que les temps aléatoires $T_A$ et $T_B$ ne sont pas indépendants. C'est d'ailleurs ce qui fait l'intérêt de la question posée (Que se passerait-il si $T_A$ et $T_B$ étaient indépendants?).

On peut montrer que si $\sigma^2=Id$, alors la loi du couple $(T_A,T_B)$ est identique à celle du couple $(T_B,T_A)$. En effet on a:

$$ T_A=\min(t^1_A,t^2_A),\quad T_B=\min(\sigma(t^1_A),\sigma(t^2_A)) $$

Donc, en utilisant le fait que la loi de $(t^1_A,t^2_A)$ est identique à celle de $(\sigma(t^1_A),\sigma(t^2_A))$, on obtient:

$$ \begin{align*} \mathbb{P}\left(T_A=k,T_B=l\right) & = \mathbb{P}\left(\min(t^1_A,t^2_A)=k,\min(\sigma(t^1_A),\sigma(t^2_A))=l\right)\\ & = \mathbb{P} \left(\min(\sigma(t^1_A),\sigma(t^2_A))=k, \min(\sigma^2(t^1_A),\sigma^2(t^2_A))=l\right). \end{align*} $$

Et lorsque $\sigma^2=Id$, on en déduit $\mathbb{P} \left(T_A=k,T_B=l\right) = \mathbb{P}(T_B=k,T_A=l)$.

Ceci permet d'en déduire (exercice simple mais instructif) que $$ \mathbb{P}(T_A<T_B)=\mathbb{P}(T_B<T_A). $$

La relation $\sigma^2=Id$ est vérifiée lorsque $p=q$ (on peut le vérifier à l'aide du code ou le prouver si on est courageux). Ce qui prouve le résultat (attendu !) que lorsque $p=q$ le jeux est équilibré.