4.1 Composition et délégation

On souhaite à présent modéliser plusieurs classes d'objets géométriques : les points, les cercles et les rectangles. Un point du plan est défini par ses deux coordonnées, un cercle est défini par son centre et son rayon, un rectangle est défini par ses points supérieur gauche et inférieur droit. Voici par exemple la construction de deux points, d'un cercle et d'un rectangle, en supposant que les classes correspondantes ont été définies :

package geometrie;

class TestFormes {
  public static void main(String[] args) {
    Point o1 = new Point(), 
          o2 = new Point(), 
          p = new Point(1,1);
    Cercle c = new Cercle(o1, 2);              
    Rectangle r = new Rectangle(o2, p);        
  }
}

Figure: Objets définis par composition.

Il n'y a pas de difficulté pour définir ces classes dans le paquet geometrie (on notera que si ces classes devaient être déclarées publiques, il faudrait les définir dans des unités de compilation distinctes, chacune portant le nom de sa classe) :

package geometrie;

class Cercle {
  Point centre;
  double rayon;
  Cercle(Point centre, double rayon) {
    this.centre = centre;
    this.rayon = rayon;
  }
  // ...
}

class Rectangle {
  Point sg, id;
  double rayon;
  Rectangle(Point sg, Point id) {
    this.sg = sg;
    this.id = id;
  }
  // ...
}

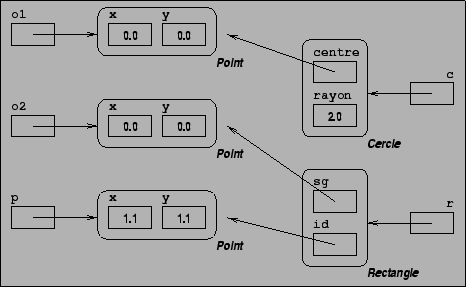
On notera que la classe Cercle a un champ centre dont le type, Point est une classe. Ceci ne signifie pas qu'un objet de type Cercle contienne un objet de type Point. La valeur d'un champ est toujours une valeur, ce ne peut pas être un objet ; la valeur de centre est une référence à un objet (figure ). De la même façon, la classe Rectangle a deux champs sg et id de type Point qui désignent les sommets « supérieur gauche » et « inférieur droit » du rectangle. Les instances des classes Cercle et Rectangle sont des exemples d'objets composés à partir d'autres objets (ici, des points). Il est fréquent qu'une classe soit définie par composition à partir d'autres classes.

Nous allons définir une méthode de translation pour ces objets. Pour translater un cercle, il suffit de translater son centre ; pour translater un rectangle, il suffit de translater ses sommets. On dit que l'on délègue une méthode à d'autres objets, ici ses composants.

package geometrie;

class Cercle {
  // ...
  void translater(double dx, double dy) {
    centre.translater(dx, dy);
  }
}

class Rectangle {
  // ...
  void translater(double dx, double dy) {
    sg.translater(dx, dy);
    id.translater(dx, dy);
  }
}

Ces deux techniques, de composition et de délégation, sont très utilisées. Par exemple, on définit une « interface graphique » à partir de plusieurs « composants graphiques » (des boutons, barres de menus, menus, etc.) et on délégue à des « observateurs » le soin de traiter certains événements (presser un bouton, choisir un item dans un menu, etc.).

Voici un autre exemple. Nous devons définir une classe PointColore, dont les instances sont des points colorés^4.1, que l'on peut translater. Une solution consiste à procéder par composition des classes java.awt.Color (la classe Color du paquet java.awt) et Point et à déléguer la translation au composant de type Point :

package geometrie;

class PointColore {
 Point point;
 java.awt.Color couleur;

 PointColore(double x, double y, java.awt.Color couleur) {
   point = new Point(x, y);
   this.couleur = couleur;
 }
 void translater(double dx, double dy) {
   point.translater(dx, dy);
 }
}

Cette classe utilise la classe Point, un de ses constructeurs et une de ses méthodes. On peut l'utiliser ainsi :

package geometrie;

class Test {
 public static void main(String[] args) {
   PointColore pointRouge = 
     new PointColore(1, 2, java.awt.Color.red);
   pointRouge.translater(1, 1);
 }
}