Cryptographie à clé publique : RSA

La cryptographie a pour but d'assurer la sécurité des données, en les chiffrant afin de les rendre incompréhensibles sans l'usage d'une clé de déchiffrement. L'exponentielle modulaire intervient dans les algorithmes de la cryptographie à clé publique, car l'exponentielle modulaire est considérablement plus facile à calculer que son inverse, le logarithme modulaire. Le système de chiffrement à clé publique RSA a été proposé en 1977 par Ron Rivest, Adi Shamir et Leonard Adleman.

Pour construire ses clés, chaque utilisateur de RSA

• choisit deux grands nombres premiers $p$ et $q$
• calcule $n=pq$
• choisit un entier $e<n$ qui est premier avec $(p-1)(q-1)$
• calcule l'inverse $d$ de $e$ modulo $(p-1)(q-1)$
• publie sa clé publique, qui est formée des deux entiers $e$ et $n$
• conserve sa clé privée $d$
• détruit les entiers $p$ et $q$ qui ne doivent pas être divulgués.

Les fonctions de chiffrage et de déchiffrage sont respectivement:

$$\begin{eqnarray*} C(m) &= &m^e \mathop{\normalfont\mathrm{mod}}\nolimits n \\ D(m) &= &m^d \mathop{\normalfont\mathrm{mod}}\nolimits n \end{eqnarray*}$$

Quand $A$ veut communiquer un entier $m$ ($0<m<n$) à $B$, il calcule $C_B(m)$ à l'aide de la clé publique de $B$, qu'il envoie à $B$ ; à la réception d'un message chiffré $c$, $B$ calcule $D_B(c)$ à l'aide de sa clé privée. Il s'agit bien d'un déchiffrage car $D(C(m)) = C(m)^d \mathop{\normalfont\mathrm{mod}}\nolimits n = m^{ed}\mathop{\normalfont\mathrm{mod}}\nolimits n = m$, grâce au théorème d'Euler $m^{\phi(n)} = 1 \mathop{\normalfont\mathrm{mod}}\nolimits n$ si $m$ est premier avec $n$, et au fait que $\phi(n)=(p-1)(q-1)$.

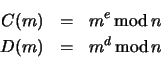
La sécurité provient de la difficulté à factoriser de grands entiers. En effet, déterminer $d$ à partir de $e$ demande la connaissance de $(p-1)(q-1)$; or la publication de $n=pq$ n'est en aucune façon une aide pour calculer $(p-1)(q-1)$, qui ne peut être obtenu qu'à partir de $p$ et $q$. D'autre part, on ne sait pas calculer efficacement des racines $e$-ièmes, ce qui permettrait d'avoir le texte clair $m$ à partir du texte chiffré $C(m)$.