On veut déplacer, à l’aide d’un système de levage par câble (grue ou pont roulant), une charge d’un endroit à un autre en évitant les oscillations résiduelles à l’arrivée.
L’objectif est de proposer une stratégie de commande simple et réaliste qui repose sur une structure de commande hiérarchisée, composée de régulateurs de bas niveau rapides, simples et découplés et d’une commande de haut niveau lente et prenant en compte les couplages.
En outre, on mesure la position et la vitesse du chariot ainsi que la position et la vitesse du treuil, mais la position de la charge n’est pas mesurée. C’est pourquoi nous ne considérons dans tout ce TP que des bouclages qui ne dépendent que des positions et vitesses du chariot et du treuil.
Un chariot de masse M roule sur l’axe OX, supposé représenter la flèche de la grue ou le pont s’il s’agit d’un pont roulant. Sa position est notée x. Un moteur exerce sur lui une force horizontale d’intensité F. Le chariot porte en outre un treuil de rayon ρ autour duquel s’enroule un câble assurant le levage de la charge située à son extrêmité. La position de la charge dans le repère XOZ est notée (ξ,ζ) et sa masse est égale à m. Le couple exercé sur le treuil par un second moteur est noté C. La longueur du câble, sa tension et l’angle par rapport à la verticale sont notés R, T et 𝜃 respectivement. On se place dans la configuration où R < R0 pour éviter que la charge ne traîne par terre, et on suppose que la tension du câble T est toujours positive. On adopte en outre la convention de signe pour 𝜃 : 𝜃 ≤ 0 si ξ ≤ x et 𝜃 > 0 sinon.
Les équations du mouvement sont les suivantes :
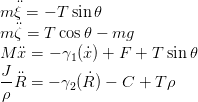 | (1) |
et les contraintes géométriques entre les coordonnées des deux corps sont données par :
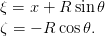 | (2) |
Pour les simulations, nous aurons besoin de la forme explicite de (1), donnée (voir le polycopié section 7.1) par
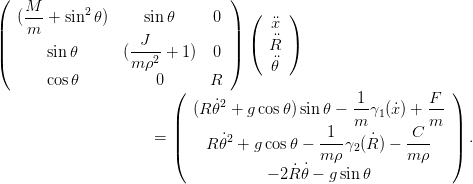 | (3) |
Posons
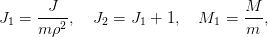
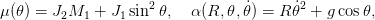
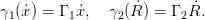
![[ ( ) ]
¨x = --1-- J α (R,𝜃, ˙𝜃)sin 𝜃 + sin𝜃- C + Γ R˙ + J2-(F − Γ ˙x)
μ (𝜃) [ 1 m ρ 2 m 1
1 (M1 + sin2 𝜃)( )
¨R = ----- M1 α(R, 𝜃, ˙𝜃) −------------- C + Γ 2R ˙
μ(𝜃) m ρ ]
− sin-𝜃-(F − Γ 1˙x)
[ m ]
¨ -cos𝜃- ˙ sin-𝜃( ˙) J2-
𝜃 = − R μ(𝜃) J1α(R, 𝜃,𝜃)sin𝜃 + m ρ C + Γ 2R + m (F − Γ 1˙x)
1 ( )
− -- 2 ˙R𝜃˙+ g sin 𝜃 .
R](grue7x.png) | (4) |
Pour les simulations, on utilise les valeurs suivantes :
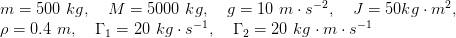
Comme annoncé à la section précédente, on mesure les positions x et R ainsi que leurs vitesses
ẋ et Ṙ mais on ne mesure ni 𝜃 ni 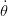 . Les bouclages ne devront donc dépendre que de x, ẋ, R et
Ṙ.
. Les bouclages ne devront donc dépendre que de x, ẋ, R et
Ṙ.
Pour le problème de manutention qui nous intéresse, nous ne considèrerons que des déplacements arrêt-arrêt, c’est-à-dire partant du repos et arrivant au repos, avec des durées de transfert assez courtes. Pour cela, on dispose de moteurs suffisamment puissants, ce qui évite d’imposer des limitations sur la force et le couple que le moteur et le treuil sont capables de produire.
Par contre, les coefficients Γ1 et Γ2 sont très mal connus (les frottements sont des phénomènes difficiles à décrire quantitativement) et seront ignorés pour la mise au point de lois de commande. Par contre, ils sont pris en compte par le programme de simulation.
On suppose dans un premier temps que l’angle 𝜃 varie suffisamment peu autour de 0, de
même que la vitesse angulaire 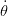 , ce qui permet, d’après (2), de considérer que x ≈ ξ et
z ≈−R.
, ce qui permet, d’après (2), de considérer que x ≈ ξ et
z ≈−R.
On se propose alors de déplacer la charge en ligne droite depuis la position initiale ξi = xi,
ζi = −Ri à l’instant ti, avec 𝜃(ti) = 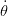 (ti) = 0,
(ti) = 0, 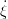 (ti) = ẋ(ti) = 0, Ṙ(ti) = −
(ti) = ẋ(ti) = 0, Ṙ(ti) = −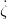 (ti) = 0, jusqu’à la
position finale ξf = xf, ζf = −Rf à l’instant tf, avec 𝜃(tf) =
(ti) = 0, jusqu’à la
position finale ξf = xf, ζf = −Rf à l’instant tf, avec 𝜃(tf) = 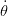 (tf) = 0,
(tf) = 0, 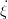 (tf) = ẋ(tf) = 0,
Ṙ(tf) = −
(tf) = ẋ(tf) = 0,
Ṙ(tf) = −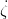 (tf) = 0 (voir figure 2), avec des vitesses ẋ et Ṙ suffisamment faibles (déplacement
quasi-statique).
(tf) = 0 (voir figure 2), avec des vitesses ẋ et Ṙ suffisamment faibles (déplacement
quasi-statique).
La trajectoire de référence de la charge est donnée par :
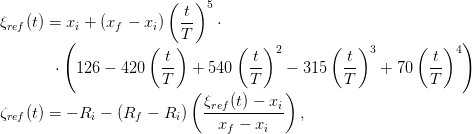 | (5) |
celle du chariot par xref(t) = ξref(t) et celle de la longueur de câble par Rref(t) = −ζref(t).
On peut choisir la durée T pour assurer que l’écart entre x et ξ et entre ζ et −R soit suffisamment petit.
Dans tout ce qui suit, le déplacement est caractérisé par
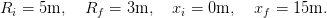
On introduit en outre les deux bouclages suivants pour assurer le suivi de trajectoire : l’un sur F de façon à asservir la position x et la vitesse ẋ à leur consigne xref et ẋref, l’autre sur C de façon à asservir R et Ṙ à leur consigne Rref et Ṙref :
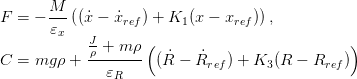 | (6) |
où K1 et K3 sont des gains et 𝜀x et 𝜀R des constantes de temps, qu’il s’agit de régler pour assurer le suivi désiré.
À la place des approximations de la question précédente, on calcule la trajectoire de référence exacte de x et R, donnée par (voir cours)
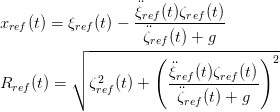 | (7) |
avec ξref et ζref toujours donnés par (5).
On veut maintenant éviter un obstacle situé vers le milieu de la trajectoire de la charge
comme indiqué figure 3. Plus précisément, on veut que la charge passe par le point
(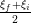 , 2ζf − ζi) qui doit être le maximum de la courbe suivie par la charge entre ξi et
ξf.
, 2ζf − ζi) qui doit être le maximum de la courbe suivie par la charge entre ξi et
ξf.
On vérifie (voir cours) que la trajectoire polynômiale suivante :
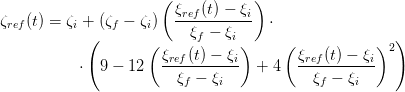 | (8) |
avec ξref donné par (5), satisfait les conditions posées.
On recalcule alors les références de x et R en utilisant (7) et la commande (6).
Question 3 Reprendre la même étude que précédemment en exécutant le fichier Grue2.sci. Que constate-t-on si l’on cherche à diminuer T ? Expliquer.