Décision optimale en économie :
problème de consommation-investissement
Les questions

Luc Doyen
(last modiﬁcation date: October 10, 2017)

Version pdf de ce document
Version sans bandeaux

1 Présentation du problème
2 Cas déterministe: rendement certain
3 Cas aléatoire: rendement incertain

1 Présentation du problème
2 Cas déterministe: rendement certain
2.1 Solution analytique dans le cas exponentiel
2.2 Application numérique sous Scilab
3 Cas aléatoire: rendement incertain
3.1 Le cas isoélastique
3.2 Application numérique Scilab

1 Présentation du problème

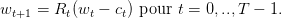
On considère un consommateur souhaitant utiliser de manière optimale sa richesse sur T périodes. Sa richesse à l’instant t est notée w_t et sa consommation sur la période [t,t + 1[ est notée c_t. On suppose que la richesse non consommée à l’instant t est investie dans un portefeuille ﬁnancier de rendement R_t ce qui donne la dynamique suivante:

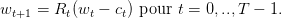wt+1 = Rt(wt − ct) pour t = 0,..,T − 1.

(1)

Le bien-être du consommateur est représenté par la somme actualisée des utilités de ses consommations successives et de la richesse ﬁnale:

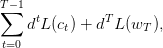
T∑ −1 dtL(ct) + dTL (wT ), t=0

où d est un facteur d’actualisation et L(.) une fonction d’utilité.

2 Cas déterministe: rendement certain

On suppose tout d’abord que le portefeuille est constitué d’un actif sans risque ou de rendement certain R:

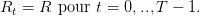
Rt = R pour t = 0,..,T − 1.

Le consommateur souhaite optimiser son bien-être soit

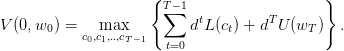
{ } T∑ −1 t T V (0,w0) = c ,cma,.x.,c d L(ct) + d U (wT) . 0 1 T−1 t=0

2.1 Solution analytique dans le cas exponentiel

On suppose maintenant que l’utilité est de type exponentielle

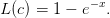
− x L (c) = 1 − e .

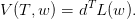
Que vaut la fonction valeur à l’instant ﬁnal V (T,w) ? $V (T,w ) = dTL (w ).$
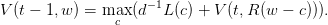
Quelle est la relation de récurrence liant les fonctions valeurs V (t − 1,.) et V (t,.)? $V (t − 1,w ) = max (d−1L (c) + V (t,R (w − c))). c$
Montrer que, si on dispose au temps t d’une richesse w, la consommation optimale c^∗(t,w) et la fonction valeur V (t,w) satisfont
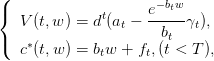$( −btw { V (t,w ) = dt(a − e----γ ), t bt t ( c∗(t,w ) = btw + ft,(t < T ),$ (2)

où les paramètres a_t,b_t,f_t,γ_t sont déﬁnis par la récurrence

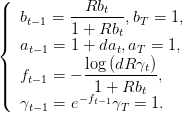$( || b = --Rbt--,b = 1, ||| t− 1 1 + Rbt T { at− 1 = 1 + dat,aT = 1, | log (dR γt) ||| ft− 1 = − ----------, |( −f1t− +1 Rbt γt− 1 = e γT = 1.$ (3)
En déduire que les consommations optimales en boucle fermée c_t^∗ satisfont la relation:
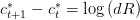$c∗t+1 − c∗t = log(dR )$ (4)

Donner alors des conditions sur d et R pour que les consommations optimales soient croissantes dans le temps.
$dR ≥ 1.$
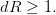
Que se passe-t-il en particulier si dR = 1 ?

2.2 Application numérique sous Scilab

Question 1 Ouvrir un ﬁchier nom_de_fichier.sce et y recopier les paramètres suivant.

Construire les vecteurs B et F donnés par l’équation (3).

 
  //paramètres 
  Horizon=4; 
  R=1.1;// rendement certain 
  w0=10;// richesse initiale 
  d=0.8;// facteur d'actualisation 
   
  // Construction de B et F 
   
  B(Horizon + 1)=1; 
  F(Horizon + 1)=0; 
   
  for t=Horizon :  -1 :  1 do 
    B(t)=R * B(t + 1) / (1 + R * B(t + 1)); 
    F(t)=(-log(d * R) + F(t + 1)) / (1 + R * B(t + 1)); 
  end;

Question 2 Créer alors les vecteurs de richesses et consommations optimales Wopt et Copt en utilisant la dynamique (1) et l’équation (2) du feedback.

Tracer trajectoire et décisions optimales en fonction du temps, à l’aide des commandes Scilab plot et plot2d2.

 
  // Consommation et richesse optimales 
   
  Wopt(1)=w0; 
  for t=1 : Horizon do 
    Copt(t)=B(t) * Wopt(t) + F(t); 
    Wopt(t + 1)=R * (Wopt(t) - Copt(t)); 
  end; 
   
  // Affichage 
  xbasc(); 
  plot(Copt);plot(Wopt);

Question 3 Répéter l’opération précedente pour diﬀérentes valeurs du facteur d’actualisation d entre 0.5 et 1. Quel résultat retrouvez-vous ?

On retrouve le lien entre dR et la croissance de consommation.

Question 4 Charger dynoptim et consulter le help. Déﬁnir la dynamique f et ses dérivées partielles f_w par rapport à l’état et f_c par rapport à la commande. Faire de même avec le coût instantané et le coût ﬁnal. Écrire les contraintes sur les commandes.

 
  exec "SCI/contrib/dynoptim-1.3/loader.sce" 
  // salle élèves ENPC 
  exec("/home/s/scilab-contrib/dynoptim-1.2/loader.sce"); 
  // CERMICS 
  help "dynoptim" 
   
  //dynamique 
  function z=f(c,w,t) z=R * (w - c),endfunction; 
  function D=f_w(c,w,t) D=R,endfunction; 
  function D=f_c(c,w,t) D=-R,endfunction; 
   
  // contrainte controles 
   
  c_min=zeros(1,Horizon); 
  c_max=zeros(1,Horizon) + exp(100);

 
  // Fonction utilité 
   
  function z=Utilite(x) z=1 - exp(-x),endfunction; 
  function D=DUtilite(x) D=1 * exp(-x),endfunction; 
   
  // cout intégral 
  function z=L(c,w,t) z=-(d ^ t) * Utilite(c),endfunction; 
  function D=L_w(c,w,t) D=0,endfunction; 
  function D=L_c(c,w,t) D=-(d ^ t) * DUtilite(c),endfunction; 
   
   
  // cout final 
  function z=g(w,t) z=-(d ^ t) * Utilite(w),endfunction; 
  function D=g_w(w,t) D=-(d ^ t) * DUtilite(w),endfunction;

Question 5 Choisir une richesse initiale w0. Initialiser l’algorithme d’optimisation dynamique dynoptim avec un vecteur c_init. Faire un appel à dynoptim et tracer les solutions. Vériﬁer que les solutions coïncident avec celles des Questions précédentes.

 
  //conditions initiales 
  w0=[10]; 
  c_init=w0 / (Horizon + 1) + zeros(1,Horizon); 
   
  // Appel dynoptimsc 
   
  L_noms=["L","L_c","L_w"]; 
  f_noms=["f","f_c","f_w"]; 
  g_noms=["g","g_w"]; 
   
  [c_opt,w_opt]=dynoptim(L_noms,f_noms,g_noms,c_min,c_init,c_max,w0), 
   
  //xbasc() 
  plot2d(c_opt); 
  plot2d(w_opt)

Question 6 Que constatez-vous en faisant varier le facteur d’actualisation d entre 0.5 et 1 ?

On retrouve le lien entre dR et la croissance de consommation.

3 Cas aléatoire: rendement incertain

On suppose maintenant que le portefeuille de rendement R_t est constitué d’un actif risqué dont le rendement est noté A et d’un actif sans risque de rendement B. On appelle α_t la proportion d’actif non risqué dans le portefeuille à la période t:

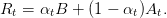
Rt = αtB + (1 − αt)At.

Pour simpliﬁer, on suppose que les variables aléatoires (A_t) sont indépendantes et de même loi.

On suppose que le consommateur optimise l’espérance de la somme actualisée des utilités de ses consommations successives et de la richesse ﬁnale :

{T −1 } V (0,w ) = sup 𝔼 ∑ dtL (c) + dTL (w ) . 0 ({ t T c0,c1,..,cT−1 t=0 ( α0,α1,..,αT−1

où c_t et α_t correspondent à une stratégie.

3.1 Le cas isoélastique

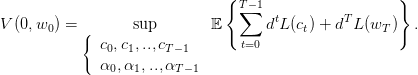
On suppose que L(x) = x^γ.

Montrer que l’équation de Bellman s’écrit
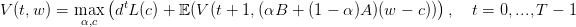$( ) V (t,w ) = max dtL (c) + 𝔼 (V(t + 1,(αB + (1 − α)A )(w − c)) , t = 0,...,T − 1 α,c$ (5)

où A est une variable aléatoire de même loi que la loi commune des (A_t).
Montrer, par récurrence, que la consommation optimale c^∗(t,w), le portefeuille optimal α^∗(t) et la fonction valeur V (t,w) satisfont à
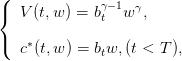$({ γ−1 γ V(t,w ) = bt w , ( ∗ c(t,w ) = btw, (t < T),$ (6)

et

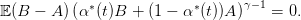$∗ ∗ γ−1 𝔼(B − A) (α (t)B + (1 − α (t))A ) = 0.$ (7)
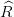Donner l’équation de récurrence satisfaite par b_t. On utilisera l’équivalent certain du portefeuille optimal obtenu précédemment c’est à dire
$L(R^) := 𝔼 [L(R ∗)] avec R∗ = α ∗B + (1 − α ∗)A.$ (8)

et le terme
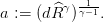
$^ γ -1- a := (dR )γ−1.$

3.2 Application numérique Scilab

Question 7 Ouvrir un ﬁchier nom_de_fichier.sce et y recopier les paramètres suivants. Écrire une fonction Scilab util pour la fonction d’utilité puissance x^γ.

  //paramètres
  puis=0.5;
  // exposant gamma de la fonction d'utilité
  Horizon=10;
  B=1.1; d=1/B;
  w0=10;

Question 8 On suppose que le rendement risqué A suit une loi du type

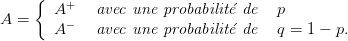
{ A+ avec une probabilitˊe de p A = A− avec une probabilitˊe de q = 1 − p.

Montrer alors que la solution de (7) est donnée par

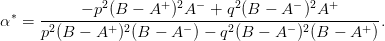
∗ -----−-p2(B-−--A+-)2A−-+-q2(B--−-A−-)2A+------- α = p2(B − A+ )2(B − A− ) − q2(B − A − )2(B − A+ ).

Sous Scilab, choisir les paramètres suivants pour p,q,A⁺,A⁻. Calculer la proportion optimale d’actif non risqué α^∗.

  // Données sur la variable aléatoire A
  p=0.5; q=1-p;
  Aplus=1.3;Amoins=1;

Question 9 Construire alors le vecteur b donné par l’équation (6) en utilisant l’équivalent certain du portefeuille optimal 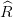et le paramètre a. On déﬁnira pour cela une fonction Scilab Ropt qui à un rendement A associe le rendement optimal du portefeuille.

Question 10 Écrire une fonction Scilab dyn-opt qui, à une richesse w et à une valeur A du rendement risqué, associe la richesse au pas de temps suivant résultant de l’application de la commande optimale (c^∗(t,w),α^∗).

Pour cela, on écrira une fonction Scilab cons-opt qui, à une richesse w, associe la consommation optimale c^∗(t,w) en boucle fermée.

Question 11 Écrire une procédure de simulation de la variable aléatoire A. Réﬂéchir à une écriture vectorielle (plus rapide), sans test, utilisant la fonction Scilab sign.

Question 12 À partir de w₀, générer une trajectoire optimale stochastique w^∗(t) de richesses. Tracer les trajectoires t(w^∗(t),c^∗(t)) pour une réalisation de A.

Question 13 Écrire une procédure Scilab fournissant N réalisations des variables aléatoires J(u^∗(.)), w^∗(t) et c^∗(t). En déduire des valeurs approchées pour leur moyenne et variance. Donner un histogramme de J(u^∗(.)).

Décision optimale en économie : problème de consommation-investissement Les questions

Contents