Minimisation de coûts d’abattement de gaz à eﬀet de serre
Optimisation dynamique
Les questions

Sébastien Berthaud
(last modiﬁcation date: October 10, 2017)

Version pdf de ce document
Version sans bandeaux

1 L’optimisation dynamique sans contrainte
2 Analyse économique de mesures de prévention du changement climatique
3 L’optimisation dynamique avec contrainte de borne sur l’état

1 L’optimisation dynamique sans contrainte
2 Analyse économique de mesures de prévention du changement climatique
2.1 Coûts et contraintes
2.2 Coûts d’abattement
2.3 Coûts des dommages
2.4 Équation d’état
2.5 Données
2.6 Un problème d’optimisation dynamique
3 L’optimisation dynamique avec contrainte de borne sur l’état

1 L’optimisation dynamique sans contrainte

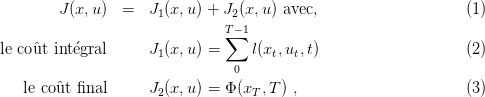
On veut résoudre ici un problème, appelé problème d’optimisation de Bolza, et qui se présente sous la forme suivante :

Soit T > 0 (éventuellement T = +∞), on minimise en x₀,…,x_T ∈ ℝⁿ,
et en u₀,…,u_T−1 ∈ ℝ^p, le critère

J(x,u ) = J1(x,u ) + J2(x, u) avec, (1) T−1 ∑ le coˆut int´egral J1(x,u ) = l(xt,ut,t) (2) 0 le couˆt ﬁnal J2(x,u ) = Φ(xT ,T) , (3)

en tenant compte de la dynamique

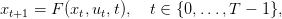xt+1 = F (xt,ut,t), t ∈ {0,...,T − 1},

(4)

et éventuellement d’un domaine d’admissibilité

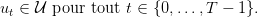ut ∈ 𝒰 pour tout t ∈ {0,...,T − 1 }.

(5)

La variable u est la commande, c’est la variable sur laquelle on peut agir. La variable x est l’état : si l’on ﬁxe l’état initial x₀, et si l’on connaît la commande u_t à chaque instant t, alors on peut retrouver l’état x_t à tout instant via la dynamique F.

Question 1 Résoudre le problème suivant grâce à la fonction dynoptim.

On cherche

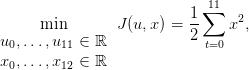
11 1∑ 2 min J(u,x ) = 2 x , u0,...,u11 ∈ ℝ t=0 x0,...,x12 ∈ ℝ

en tenant compte de la dynamique

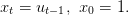
xt = ut−1, x0 = 1.

2 Analyse économique de mesures de prévention du changement climatique

2.1 Coûts et contraintes

Une politique de réduction des émissions de co₂ (gaz à eﬀet de serre) doit arbitrer entre diﬀérents coûts et contraintes :

le coût des dommages futurs des changements climatiques, supposé être une fonction d(M_t,t) de la seule concentration M_t en co₂ ;
le coût des mesures de réduction des émissions, supposé être une fonction C(a_t,t) du seul abattement a_t ;
d’éventuelles contraintes imposées à la concentration M_t, du type M_t ≤M.

Cet arbitrage est réalisé sur un certain nombre T (également appelé horizon) de pas de temps (années ou dizaines d’années, qui va ici de 1990 à 2110).

On suppose que les émissions de référence E_t, c’est à dire l’évolution des émissions si aucune mesure n’est prise, sont connues. On dispose de moyens pour réduire à l’instant t les émissions d’une fraction a_tE_t : a_t est appelé abattement. On note M_t la concentration de gaz à eﬀet de serre à l’instant t.

L’objectif consiste à minimiser la somme actualisée (à un taux ρ > 0) des coûts sur l’horizon T, qui forme un critère J, fonction de l’état M_t et de la commande a_t, qui s’écrit de la manière suivante :

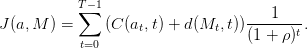T∑− 1 1 J (a,M ) = (C (at,t) + d(Mt, t))-------t. t=0 (1 + ρ)

(6)

2.2 Coûts d’abattement

Le coût d’abattement s’écrit

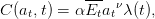--- C (at,t) = αEtat νλ(t),

(7)

et il est composé de trois facteurs

un terme dépendant de a_t en αE_ta_t^ν qui est le coût d’abattement ¡¡brut¿¿ ;
un terme de progrès technique λ(t), où λ est une fonction décroissante vériﬁant λ(0) = 1 et lim _t→∞λ(t) = λ (0 < λ < 1).

On prend ici

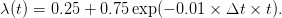λ (t) = 0.25 + 0.75exp (− 0.01 × Δt × t).

(8)

Cette fonction simule les conséquences du progrès technique en faisant décroître le coût des mesures de réductions des émissions avec le temps : on considère que les méthodes utilisées s’améliorent avec le temps, d’où des baisses de coût.

2.3 Coûts des dommages

On déﬁnit la fonction dommage comme suit :

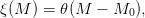ξ (M ) = 𝜃(M − M0 ),

(9)

où 𝜃 est un réel ﬁxé et M₀ désigne la concentration en CO₂ à l’instant initial.On prendra 𝜃 = 0.0 000 526 unité par ppm.

On rappelle que κ(t) désigne le pib du pays à l’instant t ; il est déﬁni de la manière suivante :

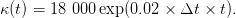κ (t) = 18 000 exp(0.02 × Δt × t).

(10)

Le terme correspondant au coût des dommages s’écrit comme le produit du pib κ(t) de référence et d’un indicateur de dommage ξ(M) variant entre 0 et 1, soit :

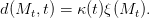d(Mt, t) = κ(t)ξ(Mt).

(11)

2.4 Équation d’état

L’évolution de la concentration en co₂ dans l’atmosphère au cours du temps est modélisée par la dynamique d’accumulation du CO₂ suivante :

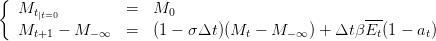{ Mt = M0 |t=0 --- Mt+1 − M − ∞ = (1 − σΔt )(Mt − M − ∞) + Δt βEt(1 − at)

(12)

où

M_−∞ est la concentration en co₂ présent dans l’atmosphère avant l’ère industrielle ;
M₀ est la concentration initiale en co₂, supposée supérieure à la concentration pré-industrielle (M₀ > M_−∞) ;
β représente la fraction (0 < β < 1) du co₂ stockée dans l’atmosphère ;
σ est une fraction (0 < σ < 1) du co₂ réabsorbée par le sol et les océans ;
E_t représente les émissions de référence, c’est-à-dire l’évolution des émissions si aucune mesure n’est prise, suposées connues (ce sont des données exogènes fournies par des scénarios) ;
E_t(1 − a_t) représente les émissions restantes après abattement.

2.5 Données

Les valeurs des paramètres utilisés par défaut sont résumées dans le tableau (2.5).


E_t	Gigatonnes par an	5.9623, 6.998, 8.4363, 9.9111,
		11.018, 12.126, 13.233, 14.541,
		15.848, 17.156, 18.463, 19.771

α	dollars par tonne de carbone et par an	1 000

ν	sans dimension	3

M₀	ppm	360

M_−∞	ppm	274

ρ	sans dimension	0.05

σ	unité par an	0.01

Δt	an	10

β	ppm par gigatonne par an	0.38

Table 1: Unités et valeurs par défaut des paramètres

2.6 Un problème d’optimisation dynamique

On est donc amené à considèrer le problème suivant : minimiser le critère

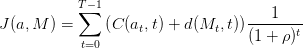T∑−1 ---1---- J(a,M ) = (C (at,t) + d(Mt, t))(1 + ρ )t t=0

(13)

avec

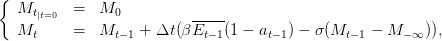
{ Mt |t=0 = M0 M = M + Δt (βE---(1 − a ) − σ(M − M )), t t−1 t−1 t−1 t−1 −∞

Question 2 Mettre en forme le problème et le résoudre grâce à la fonction dynoptim.

3 L’optimisation dynamique avec contrainte de borne sur l’état

On veut résoudre ici un problème, semblable au problème étudié précèdemment, mais avec une contrainte de borne sur l’état :

Soit T > 0 ( éventuellement T = +∞), on minimise en x₀,…,x_T ∈ ℝⁿ, et en u₀,…,u_T−1 ∈ ℝ^p, le critère

J (x,u) = J1(x,u) + J2(x,u) avec, (14) T∑− 1 le coˆut int´egral J1(x,u) = l(xt,ut,t), (15) 0 le coˆut ﬁnal J (x,u) = Φ (x ,T ) , (16) 2 T

en tenant compte de la dynamique

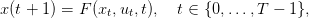x(t + 1) = F(x ,u ,t), t ∈ {0,...,T − 1}, t t

(17)

éventuellement d’un domaine d’admissibilité

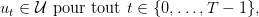ut ∈ 𝒰 pour tout t ∈ {0,...,T − 1},

(18)

et surtout de la contrainte de borne sur l’état

x ≤ x ≤ x. --

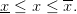(19)

La fonction dynoptimsc permet de traiter ce genre de problème.

Question 3 Reprendre le problème de politique environnementale en remplacant le coût des dommages D(M_t,t) par la contrainte explicite :

--- ∀t Mt ≤ M .

(20)

On prendra M = 600 ppm.

Minimisation de coûts d’abattement de gaz à eﬀet de serre Optimisation dynamique Les questions

Contents

1 L’optimisation dynamique sans contrainte

2 Analyse économique de mesures de prévention du changement climatique

2.1 Coûts et contraintes

2.2 Coûts d’abattement

2.3 Coûts des dommages

2.4 Équation d’état

2.5 Données

2.6 Un problème d’optimisation dynamique

3 L’optimisation dynamique avec contrainte de borne sur l’état

Minimisation de coûts d’abattement de gaz à eﬀet de serre
Optimisation dynamique
Les questions