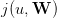Contents
1 The newsvendor problem (integer formulation)
Now, we introduce a random variable W, where W : Ω →{1, 2,…,w♯}. Here, Ω is an underlying
probability space, equipped with a probability ℙ. We suppose that the newsvendor knows the
probability distribution ℙW of the demand W.
Thus equipped, we consider the stochastic optimization problem of expected costs
minimization:
![min J(u) = 𝔼 [j(u, W )].
u∈{1,2,...,u♯} ℙ](newsvendor2x.png) | (2) |
wsharp=100;
wflat=1; demand=[wflat:wsharp]; control=[demand,1+demand($)];
cc=1;pp=10*cc;
costs=cc*control'*ones(demand)-pp*mini(ones(control')*demand,control'*ones(demand));
We will consider different demand distributions.
1.1 The demand distribution is uniform
First, we suppose that the demand distribution ℙW is uniform as follows.
probab=ones(demand); probab=probab/sum(probab);
Question 1
-
a)
- [1] Draw a histogram of the random demand W.
-
b)
- [1+1] In the scilab code above, what does the matrix costs represent? (What do
you find at the intersection of a row and of a column?) Explain in detail why we have that
criterion = probab*costs’ is a row vector made of the values of
![J (u) = 𝔼ℙ[j(u,W )]](newsvendor3x.png) for u ∈{1, 2,…,u♯}?
for u ∈{1, 2,…,u♯}?
-
c)
- [1+1] Draw the mapping u ∈ {1, 2,…,u♯}
 J(u). Thanks to the scicoslab macro
mini (that provides the minimum and the argmin index of a vector), give the numerical
value of the decision u⋆ (optimal order) that minimizes u
J(u). Thanks to the scicoslab macro
mini (that provides the minimum and the argmin index of a vector), give the numerical
value of the decision u⋆ (optimal order) that minimizes u J(u).
J(u).
-
d)
- [1+1] What does the vector decumprobab=1-cumsum(probab) represent? Explain
your answer. Check that, in agreement with the theory, we numerically have that

-
e)
- [2+1] For a given value of u, explain why the random variable
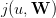 can at
most take the values
can at
most take the values 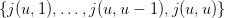 . Give, for each of the u elements
of this list, the corresponding probability that
. Give, for each of the u elements
of this list, the corresponding probability that 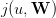 takes this value in the list. In
the end, you will provide an expression of the probability distribution of
takes this value in the list. In
the end, you will provide an expression of the probability distribution of 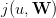 , using
probab and decumprobab.
, using
probab and decumprobab.
-
f)
- [1+2] Draw histograms of the probability distribution of the random payoff (the
opposite of the costs)
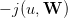 for u = u⋆ (the optimal decision) and for u = 𝔼ℙ[W]
(the naive deterministic solution consisting in ordering the mean demand 𝔼ℙ[W]). Draw
the two histograms on the same picture, so that they have the same scale. Comment on
the differences between the two histograms.
for u = u⋆ (the optimal decision) and for u = 𝔼ℙ[W]
(the naive deterministic solution consisting in ordering the mean demand 𝔼ℙ[W]). Draw
the two histograms on the same picture, so that they have the same scale. Comment on
the differences between the two histograms.
-
g)
- [1+1+1+2] The vector
grand(365,"markov",ones(probab’)*probab,1) represents a sequence of realizations
of 365 i.i.d. random variables having the same distribution than the demand W. Simulate
and draw the trajectory of the cumulated payoffs of the newsvendor during one year if,
every day, he orders the optimal quantity u = u⋆. Do the same for u = 𝔼ℙ[W] and draw
it on the same picture. In what sense does the the optimal decision u = u⋆ does better
than u = 𝔼ℙ[W]? Justify in detail why the two trajectories are approximately straight
lines; to what correspond the slopes?
-
h)
- Now, we study if the results are robusts to changes in the the ratio between the unitary
purchasing cost c and the selling price p.
-
1)
- [2] Take c < p with c ≈ p. Find the optimal decision u⋆. Draw histograms of
the probability distribution of the random payoff
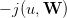 for u = u⋆ and for
u = 𝔼ℙ[W]. Simulate and draw trajectories of the corresponding cumulated payoffs.
for u = u⋆ and for
u = 𝔼ℙ[W]. Simulate and draw trajectories of the corresponding cumulated payoffs.
-
2)
- [2] Same question with c << p.
-
3)
- [2] Discuss. In particular, how does the optimal solution u⋆ vary with the ratio
c∕p?
xset("window",1);clf();plot2d2(demand,probab) xtitle("Histogram of the demand")
criterion=probab*costs';
xset("window",3);clf();plot2d2(control,criterion)
xtitle("The expected costs as function of the decision")
[lhs,optcont]=mini(criterion); disp("The optimal decision is "+string(optcont))
meandemand=probab*demand';
disp("The expected demand is "+string(round(meandemand)))
cumprobab=cumsum(probab); decumprobab=1-cumprobab;
xset("window",4);clf();plot2d2(demand,decumprobab,rect = [demand(1)-1,0,demand($),1]);
plot2d(demand,cc/pp*ones(decumprobab),style = 5); xtitle("The decumulative distribution of the demand")
disp("Is it true that "+string(cc/pp)+" lies between "+string(decumprobab(optcont))+ ...
" and "+string(decumprobab(optcont-1))+"?") NS=365;
DD=grand(NS,'markov',ones(probab')*probab,1); time=[1:NS];
xset("window",8);clf(); plot2d2(time,cumsum(-costs(round(meandemand),DD)),style = 3);
plot2d2(time,cumsum(-costs(optcont,DD)),style = 5); legends(["optimal solution "+string(optcont);
"naive deterministic solution "+string(round(meandemand))],[5,3],"lr");
xtitle("The cumulated payoffs as function of the number of days","time","payoff")
xset("window",10);clf(); uu=optcont; ss=5; plot2d2([costs(uu,[wflat:(uu-1)]),costs(uu,uu)], ...
[probab([wflat:(uu-1)]),decumprobab(uu-1)],style = ss, ...
rect = [mini(costs),0,maxi(costs),1]); uu=round(meandemand);
ss=3; plot2d2([costs(uu,[wflat:(uu-1)]),costs(uu,uu)], ...
[probab([wflat:(uu-1)]),decumprobab(uu-1)],style = ss, ...
rect = [mini(costs),0,maxi(costs),1]); legends(["optimal solution "+string(optcont);
"naive deterministic solution "+string(round(meandemand))],[5,3],"ur");
xtitle("Histograms of the costs")
1.2 The demand distribution is a mixture of two truncated Poisson distributions
Second, we suppose that the demand distribution ℙW is a mixture of two truncated Poisson
distributions as follows:
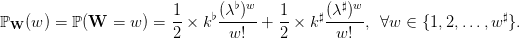 | (3) |
Question 2 [6] Same questions as in Question ?? when the demand W follows a
mixture of two truncated Poisson distributions.
lambdaflat=wsharp/4;lambdasharp=3*wsharp/4;
probabflat=(lambdaflat .^demand) ./(factorial(demand)); probabflat=probabflat/sum(probabflat);
probabsharp=(lambdasharp .^demand) ./(factorial(demand));
probabsharp=probabsharp/sum(probabsharp); probab=0.5*probabflat+0.5*probabsharp;
1.3 The demand distribution is triangular
Question 3 [6] Same questions as in Question 1 when the demand W follows a
triangular distribution over {1, 2,…,w♯}.
lambda=floor(wflat+0.3*(wsharp-wflat));
probab=[cumsum(ones([wflat:lambda]))/sum(ones([wflat:lambda])), ...
1-cumsum(ones([(lambda+1):wsharp]))/sum(ones([(lambda+1):wsharp]))]; probab=probab/sum(probab);
2 The newsvendor problem (continuous formulation)
Here, we consider that the decision can take continuous values: ![♯
u ∈ [0, u ]](newsvendor14x.png) .
.
We also adopt new notations. We suppose that the demand W can take a finite number S of
possible values Ds, where s denotes a scenario in the finite set 𝕊 (S=card(𝕊)). We denote πs the
probability of scenario s ∈ 𝕊, with
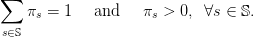 | (4) |
Notice that we do not consider scenarios with zero probability.
We consider the stochastic optimization problem
![min♯ J(u) = 𝔼 ℙ[j(u, W )].
u∈[0,u ]](newsvendor16x.png) | (5) |
We now show how to rewrite this problem as a linear program. First, we write:
Second, we deduce
Third, we conclude
This is a linear program.
Question 4 Suppose that W follows a uniform distribution over {1, 2,…,w♯}.
-
a)
- [2] Write the linear program (8) under the form adapted to the scicoslab macro
linpro.
-
b)
- [1] Solve (8) with linpro and obtain the solution to the stochastic optimization
problem (5).
-
c)
- [1] Compare with the optimal solution of Question 1.
-
d)
- [2] Increase the number w♯ of values taken by the demand W. When can you no
longer solve numerically? Compare with the result of Question 1.
3 The newsvendor problem with risk (continuous formulation)
Let λ ∈]0, 1[, that plays the role of a risk level. The Value at Risk of the cost X at level λ ∈]0, 1[
is
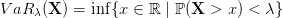
The Tail Value at Risk of the cost X at level λ ∈]0, 1[ is
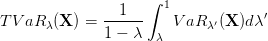
We have the limit cases:
The Rockafellar-Uryasev formula establishes that
![{ + }
T VaR λ[X ] = inf 𝔼[(X-−--s)-]+ s , λ ∈ [0, 1[
s∈ℝ 1 − λ](newsvendor23x.png)
We consider the risk averse stochastic optimization problem
![min J (u) = T VaR λ[j(u,W )].
u∈[0,u♯]](newsvendor24x.png) | (9) |
We rewrite this problem as a linear program.
Question 5 Suppose that W follows a uniform distribution over {1, 2,…,w♯}.
-
a)
- [2] Write the linear program (10) under the form adapted to the scicoslab macro
linpro.
-
b)
- [1] Solve (10) with linpro and obtain the solution to the stochastic optimization
problem (9).
-
c)
- [1] Compare with the optimal solution of Question 4.
4 The newsvendor problem with backorder (continuous formulation)
Now, we suppose that the newsvendor
- pays the unitary purchasing cost c per copy, when he orders stock;
- sells a copy at price p; we have that c > p;
- can buy extra copies at the unitary backorder cost b, after he observes a demand w
larger than the initial order u; we have that b > c
- pays the unitary holding cost h for each unsold copy, when the demand w is less than
the initial order u.
Therefore, the newsvendor’s costs are
![j (u, w) = c ◟u◝◜◞+b [w-− u]+ +h [u-− w-]+ − p◟w◝◜◞ ,
order ◟ba◝ck◜orde◞r ◟ h◝o◜lding ◞ sold](newsvendor26x.png) | (11) |
where we recall that 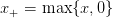 .
.
cc=0.1;pp=10*cc;bb=10*cc;hh=10*cc;
Question 6 We suppose that the demand W follows a uniform distribution over {1, 2,…,w♯}.
-
a)
- [1] Write a row vector criterion made of the values of
![J(u) = 𝔼 ℙ[j(u, W )]](newsvendor28x.png) for
u ∈{1, 2,…,u♯}.
for
u ∈{1, 2,…,u♯}.
-
b)
- [1+1] Draw the mapping u ∈ {1, 2,…,u♯}
 J(u). Thanks to the scicoslab macro
mini (that provides the minimum and the argmin index of a vector), give the numerical
value of the decision u⋆ (optimal order) that minimizes u
J(u). Thanks to the scicoslab macro
mini (that provides the minimum and the argmin index of a vector), give the numerical
value of the decision u⋆ (optimal order) that minimizes u J(u).
J(u).
-
c)
- [1] Check that, in agreement with the theory, we numerically have that
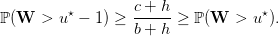
-
d)
- [1+1] For a given value of u, what is the set of values taken by the random variable
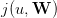 ? Give a scicoslab formula for the probability distribution of
? Give a scicoslab formula for the probability distribution of 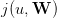 , using
probab and decumprobab.
, using
probab and decumprobab.
-
e)
- [1+1] Draw a histogram of the probability distribution of the random payoff (the
opposite of the costs)
 for u = u⋆ (the optimal decision) and for u = 𝔼ℙ[W]
(the naive deterministic solution consisting in ordering the mean demand 𝔼ℙ[W]). Draw
the two histograms on the same picture, so that they have the same scale. Comment on
the differences between the two histograms.
for u = u⋆ (the optimal decision) and for u = 𝔼ℙ[W]
(the naive deterministic solution consisting in ordering the mean demand 𝔼ℙ[W]). Draw
the two histograms on the same picture, so that they have the same scale. Comment on
the differences between the two histograms.
-
f)
- [1+1+1] Simulate the trajectory of the cumulated payoffs of the newsvendor during
one year if, every day, he orders the optimal quantity u = u⋆. Do the same for u = 𝔼ℙ[W].
Compare.
-
g)
- [4] Multiply the unitary holding cost h by a factor 5. Comment on the changes that
you observe.
-
h)
- [4] As in Section 2, write the new optimization problem as a linear program. Then,
write this latter under the form adapted to the scicoslab macro linpro. Solve with linpro
and compare with the optimal solution found above by the direct method.
-
i)
- [4] Increase the number w♯ of values taken by the demand W. When can you no
longer solve numerically? Compare with the direct method.
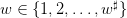 .
The variable w is called uncertainty.
.
The variable w is called uncertainty.
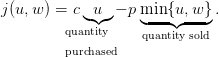
![min J(u) = 𝔼 [j(u, W )].
u∈{1,2,...,u♯} ℙ](newsvendor2x.png)
![J (u) = 𝔼ℙ[j(u,W )]](newsvendor3x.png)

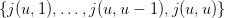
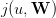
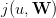
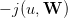
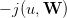
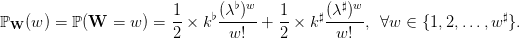
![♯
u ∈ [0, u ]](newsvendor14x.png) .
.
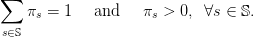
![min♯ J(u) = 𝔼 ℙ[j(u, W )].
u∈[0,u ]](newsvendor16x.png)
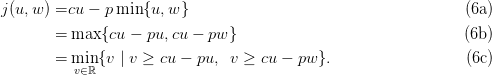
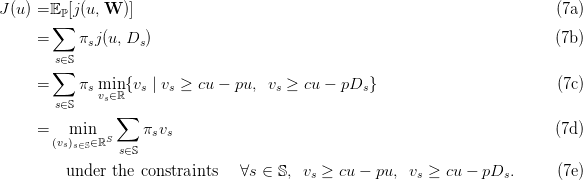
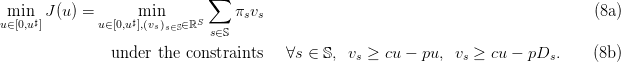
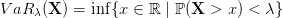
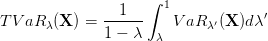
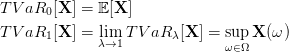
![{ + }
T VaR λ[X ] = inf 𝔼[(X-−--s)-]+ s , λ ∈ [0, 1[
s∈ℝ 1 − λ](newsvendor23x.png)
![min J (u) = T VaR λ[j(u,W )].
u∈[0,u♯]](newsvendor24x.png)
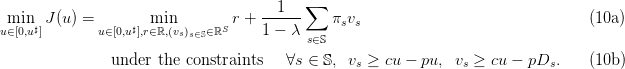
![j (u, w) = c ◟u◝◜◞+b [w-− u]+ +h [u-− w-]+ − p◟w◝◜◞ ,
order ◟ba◝ck◜orde◞r ◟ h◝o◜lding ◞ sold](newsvendor26x.png)
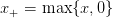 .
.
![J(u) = 𝔼 ℙ[j(u, W )]](newsvendor28x.png)