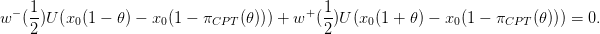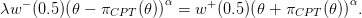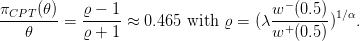Contents
We consider uncertainty modelled here by a set Ω, containing issues or scenarios. We present
some classical measures attached to a scalar prospect (random variable) X : Ω → ℝ. Here, X
represents a gain, a profit, a position, the value of a portfolio, etc., in a word a prospect while −X
represents a loss.
When focusing on situations of risk, we shall suppose that Ω carries a probability ℙ (defined on
a σ-field ℱ, so that (Ω,ℱ, ℙ) is a probability space). The expectation under probability ℙ is
denoted by 𝔼.
1 Value at Risk
The Value at Risk of a prospect X at level λ ∈]0, 1[ is
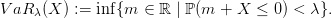 | (1) |
Intuitively, saying that the V aR5% of a portfolio is 100 means that the loss −X will be larger than
100 with probability at most 5%. However, V aR5% does not inform on the size of the
loss.
1.1 Value at Risk of a log-normal prospect
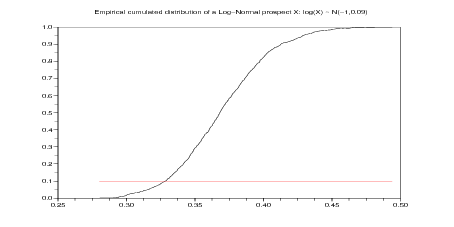
Question 1 Compute the Value at Risk at different levels (1 %, 5 %, 10 %) of a
log-normal prospect. Draw the empirical cumulated distribution of a log-normal prospect.
A prospect X is said to be log-normal if X > 0 and log X ∼𝒩(μ,σ2).
stacksize(2*10^8);
N=10^8; // number of simulations
mean=-1;
variance=0.09;
Y=grand(1,N,'nor',mean,variance) ; // simulation of a Normal r.v.
Z=sort(exp(Y));
// decreasing sort of the simulated realizations of a Log-Normal r.v.
values= Z($:-1:1) // increasing sorting
// the VaR is -quantile
lambda=0.01;
quantile=values(int(lambda*N));
disp('VaR_('+string(lambda) +')(Z)='+string(-quantile))
lambda=0.05;
quantile=values(int(lambda*N));
disp('VaR_('+string(lambda) +')(Z)='+string(-quantile))
lambda=0.10; // level
quantile=values(int(lambda*N));
disp('VaR_('+string(lambda) +')(Z)='+string(-quantile))
xset('window',10) ; xbasc(); plot2d(values,linspace(0,1,N));
plot2d(values,lambda*ones(values),style=5);
xtitle('Empirical cumulated distribution of a Log-Normal prospect X: ...
log(X) ~ N(' +string(mean) +',' +string(variance)+ ')')
xset('window',11) ; xbasc(); histplot(10,Z);
xtitle('Empirical histogram of a Log-Normal prospect X: ...
log(X) ~ N(' +string(mean) +',' +string(variance)+ ')')
1.2 Value at Risk and portfolio diversification
(Frey and McNeil, 2002)
Corporate bonds are sold at 95 $ and return 100 $ except in 2 % of cases where they lose all
value. The prospect Xi provided is thus Xi = 100𝜀i − 95 ∈{5,−95}, where ℙ(𝜀i = 1) = 0.98 and
ℙ(𝜀i = 0) = 0.02.
First, let us consider a fully concentrated portfolio C = 100X1, consisting of 100 units of the
first bond. Second, let us consider a fully diversified portfolio D = 2 ∑
i=150X
i, consisting of
2 units of each bond. The 𝜀1, …, 𝜀50 are supposed to be independent.
Question 2 Using the fact that V aR5%(𝜀1) = −1, and positive homogeneity and
translation-invariance of V aR5%, compute V aR5%(X1), then V aR5%(C). Estimate
V aR5%(D) by simulation. Conclude that withdrawing up to 500 $ from the fully concentrated
portfolio C makes it acceptable, while you need to add a capital of at least 100 $ to the fully
diversified portfolio D to make this latter acceptable.
N=1000;
bb=50; // 50 independent couples of bonds
A=rand(bb,N);
EPS= 0.5 * ( 1 + sign(A-0.02) ) ;
// an array where each column contains
// bb independent realizations of the r.v. epsilon
DD=sum( 2 * (100 * EPS - 95 ) , 'r') ;
// N realizations of the diversified portfolio D
// xset('window',12) ; xbasc(); histplot(10,DD);
// xtitle('Empirical histogram of the diversified portfolio D')
SDD=sort(DD);
values= SDD($:-1:1);
lambda=0.05;
xset('window',13) ; xbasc(); plot2d(values,linspace(0,1,N));
plot2d(values,lambda*ones(values),style=5);
xtitle('Empirical cumulated distribution ...
of the diversified portfolio DD')
VaR=-values(int(lambda*N));
disp('The Value at Risk of the diversified portfolio D is ')
disp('VaR_('+string(lambda) +')(DD)='+string(VaR))
2 Expected utility theory
The lottery  describes a hazard situation where
describes a hazard situation where
- the outcome w1 may appear with probability p1,
- …
- wn with probability pn,
where all probabilities are greater than or equal to zero and sum up to one (100% chance).
Suppose that the outcomes  are scalar. Let us be given a utility function
are scalar. Let us be given a utility function
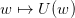 . The value of the lottery is the expectation of the utilities
. The value of the lottery is the expectation of the utilities  :
:
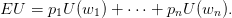
In a choice situation between two lotteries, the expected utility maximizer will select the one with
the highest EU.
2.1 Expected utility of a simple lottery
3 $
50%
-1 $50%
Question 3 Compute the expected utility of the lottery 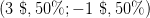 for the
utility function
for the
utility function  .
.
function v=EU(lottery,utility)
values=utility(lottery(1,:));
probabilities=lottery(2,:);
v=sum(probabilities.*values) ;
endfunction
lottery=...
[3 -1; // outcomes
0.5 0.5] ; // probabilities
function u=utility(w)
u=-%e^{-2*w};
endfunction
v=EU(lottery,utility)
2.2 Allais’ paradox
Experiment 1
Lottery 1Y 1 000 000 $ 100% versus Lottery 1Z 1 000 000 $
89%
0 $1%
5 000 000 $10%
lottery_1Z=...
[1000000 0 5000000; // outcomes
0.89 0.01 0.1] ; // probabilities
A=1;
function u=CARA(w)
u=-%e^{-A*w};
endfunction
v_1Z=EU(lottery_1Z,CARA)
gama=0.5;
function u=CRRA(w)
u= w^{1-gama}/(1-gama) ;
endfunction
v_1Z=EU(lottery_1Z,CRRA)
Experiment 2
Lottery 2Y 1 000 000 $
11%
0 $89%
versus Lottery 2Z 5 000 000 $
10%
0 $90%
Question 5 Same questions as in Question 5 for the lotteries
 and
and 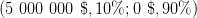 .
.
Question 6 What do you conclude from your own preferences, compared to the expected
utility evaluations of Questions 4 and 5? What is the relation with Allais’ paradox?
2.3 Bank questionnaire
In a bank questionnaire, the customer answers a series of questions ranging from 8 to 13. In
question k, he is asked which lottery he prefers between a certain lottery LOTTERY_C(k) and a
50%-50% risky lottery LOTTERY_R(k).
LOTTERY_C=list();
LOTTERY_R=list();
LOTTERY_C(8)=...
[20000; // outcomes
1] ; // probabilities
LOTTERY_R(8)=...
[40000 13400; // outcomes
0.5 0.5] ; // probabilities
LOTTERY_C(9)=...
[20000; // outcomes
1] ; // probabilities
LOTTERY_R(9)=...
[40000 10000; // outcomes
0.5 0.5] ; // probabilities
LOTTERY_C(10)=...
[20000; // outcomes
1] ; // probabilities
LOTTERY_R(10)=...
[40000 16000; // outcomes
0.5 0.5] ; // probabilities
LOTTERY_C(11)=...
[3000; // outcomes
1] ; // probabilities
LOTTERY_R(11)=...
[6000 2000; // outcomes
0.5 0.5] ; // probabilities
LOTTERY_C(12)=...
[3000; // outcomes
1] ; // probabilities
LOTTERY_R(12)=...
[6000 1500; // outcomes
0.5 0.5] ; // probabilities
LOTTERY_C(13)=...
[3000; // outcomes
1] ; // probabilities
LOTTERY_R(13)=...
[6000 2400; // outcomes
0.5 0.5] ; // probabilities
Question 7 Load the function EU following Question 3. Test wether lottery LOTTERY_C(k)
is prefered to the 50%-50% risky lottery LOTTERY_R(k) for k = 8,…, 13, for the CARA utility
functions 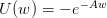 , A > 0. Compute the Arrow-Pratt coefficient of absolute risk
aversion
, A > 0. Compute the Arrow-Pratt coefficient of absolute risk
aversion 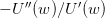 . Select a proper range of values for the parameter A. How do you
explain what you observe when the parameter A varies?
. Select a proper range of values for the parameter A. How do you
explain what you observe when the parameter A varies?
TEST_CARA=[];
for k=8:13
lottery_C=LOTTERY_C(k);
lottery_R=LOTTERY_R(k);
v_C=[];
v_R=[];
rangeA=10^(-4)*[0.3:0.5:4];
for A=rangeA
function u=CARA(w)
u=-%e^{-A*w};
endfunction
v_C=[v_C,EU(lottery_C,CARA)];
v_R=[v_R,EU(lottery_R,CARA)];
end
TEST_CARA=[TEST_CARA;v_C-v_R];
end
Question 8 Same question for the CRRA utility functions 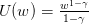 , γ > 0, γ ⁄= 1,
w > 0. Compute the Arrow-Pratt coefficient of relative risk aversion
, γ > 0, γ ⁄= 1,
w > 0. Compute the Arrow-Pratt coefficient of relative risk aversion 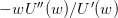 .
How do you explain what you observe when the parameter γ varies? Compare your results
with the one in the document Lettre à S. by the economist Laurent Denant-Boemont. Do you
agree with all his comments?
.
How do you explain what you observe when the parameter γ varies? Compare your results
with the one in the document Lettre à S. by the economist Laurent Denant-Boemont. Do you
agree with all his comments?
TEST_CRRA=[];
for k=8:13
lottery_C=LOTTERY_C(k);
lottery_R=LOTTERY_R(k);
v_C=[];
v_R=[];
// for gama=[0.5 1.5] //
for gama=0.05:0.2:2 // to avoid gama=1
function u=CRRA(w)
u= w^{1-gama}/(1-gama) ;
endfunction
v_C=[v_C,EU(lottery_C,CRRA)];
v_R=[v_R,EU(lottery_R,CRRA)];
end
TEST_CRRA=[TEST_CRRA;v_C-v_R];
end
TEST_CRRA
Question 9 Same question for the power-expo utility functions 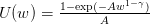 ,
1 > γ > 0, w > 0.
,
1 > γ > 0, w > 0.
TEST_SAHA=[];
for k=8:13
lottery_C=LOTTERY_C(k);
lottery_R=LOTTERY_R(k);
v_C=[];
v_R=[];
A=0.08;
// for gama=0.8
for gama=0.05:0.2:1
function u=SAHA(w)
u=(1-%e^{-A*w^(1-gama)})/A;
endfunction
v_C=[v_C,EU(lottery_C,SAHA)];
v_R=[v_R,EU(lottery_R,SAHA)];
end
TEST_SAHA=[TEST_SAHA; v_C-v_R ];
end
TEST_SAHA
2.4 Test your own relative risk aversion
(from (Gollier, 2001, p. 30)).
Suppose that you are a decision-maker who evaluates any prospect X by
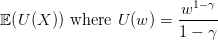 | (2) |
is a CRRA (constant relative risk aversion) utility function. The parameter γ > 0 is the relative
risk aversion parameter.
Consider the situation where you face the risk of gaining or losing a share 𝜃 of your
wealth w0 with equal probability. The relative risk premium πγ(𝜃) is implicitely defined
by
![1 1
U (w0(1 − π γ(𝜃 ))) = 𝔼 [U (w0X )] = -U (w0(1 − 𝜃)) + -U (w0 (1 + 𝜃))
2 2](risk_preferences22x.png) | (3) |
where X takes values 1 − 𝜃 and 1 + 𝜃 with equal probability 1∕2. The relative risk premium πγ(𝜃)
is the share of your wealth that you are ready to pay to escape this risk.
Question 10 Give the formula for πγ(𝜃). For each 𝜃 =5 %, 15 %, 25 %, draw the curve
giving the relative risk aversion parameter γ as a function of the relative risk premium. Fill
in the second column of Table 2.4 with your relative risk premium and compute your relative
risk aversion. Comment on what you observe.
//
theta=0.25 ;
gama=0.5:0.9:40; // avoid the value gama=1
premium=1-(0.5*(1-theta).^{1-gama}+...
0.5*(1+theta).^{1-gama}).^{1 ./(1-gama)};
xset('window',20) ; xbasc(); plot2d(premium,gama);
xtitle('Relative risk aversion parameter as function of ...
relative risk premium when theta= '+string(theta))
//=========================================================
disp("=======================================");
// istring=0;
for theta=[0.05:0.10:0.25];
str="for theta="+string(theta)+", " ;
// istring=istring+1;
yourgama=[];
for yourpremium=[0.00:0.025:0.1 0.15 0.20];
deff('y=f(gama)', 'y=1-(0.5*(1-theta).^{1-gama}+...
0.5*(1+theta).^{1-gama}).^{1 ./(1-gama)} - yourpremium' );
yourgama=[yourgama,fsolve(2,f)];
end
// mess(istring)=str+"the relative risk premium is ";
disp(str+ "to your premium")
disp(yourpremium)
disp("corresponds the relative risk aversion parameter")
disp(yourgama)
end
//=========================================================
function yourgama=mygamma(theta,yourpremium)
yourgama=[];
for j=1:(prod(size(theta)))
deff('y=f(gama)', 'y=1-(0.5*(1-theta(j)).^{1-gama}+...
0.5*(1+theta(j)).^{1-gama}).^{1 ./(1-gama)} - yourpremium(j)' );
yourgama=[yourgama,fsolve(2,f)];
end
endfunction
theta=[0.05:0.10:0.25];
yourpremium=[0.02 0.05 0.15];
disp("My likely relative risk aversion parameters are")
mygamma(theta,yourpremium)
//
|
|
|
| gaining or losing | fraction of your wealth | relative risk aversion |
| a share 𝜃 of your wealth | that you are ready to pay | parameter |
| | (empirical risk premium) | |
|
|
|
| 5 % | | |
|
|
|
| 15 % | | |
|
|
|
| 25 % | | |
|
|
|
| |
Table 1: Fill in the second column with your relative risk premium and compute your
relative risk aversion. Check the range of parameters γ obtained.
3 Cumulative Prospect Theory
3.1 Definition
(From (Kahneman and Tversky, 1979; Tversky and Kahneman, 1992))
Suppose that the prospect X takes a finite number of values
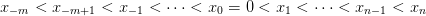 | (4) |
with corresponding probabilities (nonnegative and summing up to one)
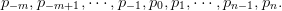 | (5) |
The evaluation of a prospect with null anchor x0 = 0 is given by
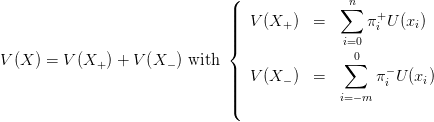 | (6) |
where U is a strictly increasing function such that U(0) = 0. When the anchor x0 is not necessarily
zero, we evaluate the prospect by V (X − x0). The weighting functions for gains and losses are
given by
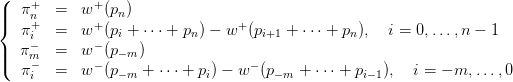 | (7) |
where w+ and w− are increasing functions satisfying w+(0) = w−(0) = 0 and w+(1) = w−(1) = 1.
In (Tversky and Kahneman, 1992), one finds
 | (8) |
with experimental evidence consistent with
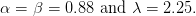 | (9) |
For the weighting functions, (Tversky and Kahneman, 1992) proposes
![+ --------pγ+--------- − ---------pγ−--------
w (p) = γ+ γ+ 1∕γ+ and w (p) = γ− γ− 1∕γ−
[p + (1 − p) ] [p + (1 − p) ]](risk_preferences30x.png) | (10) |
with parameter values
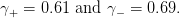 | (11) |
3.2 General Scilab code
Cumulative Prospect Theory: Scilab code
//
function w=distorsion(p,ggamma)
w= p^ggamma ./ ( ( p^ggamma + (1-p)^ggamma )^{1/ggamma} )
endfunction
ggamma_plus= 0.61;
ggamma_minus= 0.69;
function pi=weight(proba,ggamma)
cumul_proba=cumsum(proba);
distort_cumul_proba = distorsion( cumul_proba , ggamma ) ;
ip = distort_cumul_proba - [0 distort_cumul_proba(1:($-1))];
pi=ip($:(-1):1);
endfunction
alpha=0.88;
bbeta=0.88;
lambda=2.25;
function [H] = Heavyside(x)
// Heavyside function
H = bool2s(x>=0)
// notice that Heavyside(0)=1
endfunction
function u=utility(x)
u=Heavyside(x).*x^alpha - lambda* Heavyside(-x).* (-x)^bbeta
endfunction
function v=CPT_eval(lotery,anchor)
values=lotery(1,:)-anchor;
probabilities=lotery(2,:);
//
ind_plus=find(values > 0) ;
values_plus=values(values > 0) ;
proba_plus = probabilities(ind_plus);
aborp_plus=proba_plus($:(-1):1);
utility_plus=utility(values_plus) ;
weighting_plus= weight ( aborp_plus , ggamma_plus) ;
//
ind_minus=find(values <= 0) ;
values_minus=values(values <= 0) ;
proba_minus = probabilities(ind_minus);
utility_minus=utility(values_minus) ;
weighting_minus= weight ( proba_minus , ggamma_minus) ;
//
v= sum(utility_plus .* weighting_plus) + ...
sum(utility_minus .* weighting_minus)
endfunction
//
3.3 Allais’ paradox
Question 11 Same questions as in §2.2, but evaluating lotteries by CPT, with either zero
anchor, or a positive one that you will choose.
anchor=0;
v=CPT_eval(lottery_1Z,anchor)
3.4 Bank questionnaire
Question 12 Same questions as in §3.4, but evaluating lotteries by CPT, with either zero
anchor, or the value of the certain lottery.
v_C=[];
v_R=[];
for k=8:13
lottery_C=LOTTERY_C(k);
lottery_R=LOTTERY_R(k);
//
anchor=0;
anchor=lottery_C(1,:);
//
v_C=[v_C,CPT_eval(lottery_C,anchor)];
v_R=[v_R,CPT_eval(lottery_R,anchor)];
end
TEST_CPT=v_C-v_R
3.5 Relative risk aversion
Let us consider the problem in Sect. 2. Suppose that you face the risk of gaining or losing a share
𝜃 of your wealth x0 with equal probability. The relative risk premium πCPT (𝜃) is the share of your
wealth that you are ready to pay to escape this risk. Expressing indifference between this risk and
the certain prospect x0 1 − 𝜃
1 − 𝜃 gives:
gives:
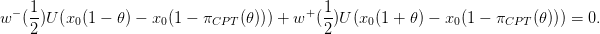 | (12) |
Notice that (8) with α = β implies that the evaluation of a prospect with respect to an anchor
is invariant with respect to a positive scaling factor (of both the prospect and the anchor). We thus
write the above equation with x0 = 1, to obtain:
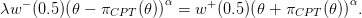 | (13) |
In the end
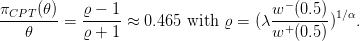 | (14) |
rho = ( lambda * weight(0.5,ggamma_minus) / ...
weight(0.5,ggamma_plus) )^{1/alpha}
factor= (rho-1)/(rho+1)
|
|
| gaining or losing a share 𝜃 of your wealth | CPT relative risk premium |
|
|
| 5 % | 2.3 % |
|
|
| 15 % | 7 % |
|
|
| 25 % | 11.6 % |
|
|
| |
Table 2: Relative risk premium evaluated by Cumulative Prospect Theory (CPT)
3.6 Compte d’épargne MMmax by Mutuelles du Mans
(From (Pfiffelmann and Roger, 2005))
The compte d’épargne MMmax was launched in November 2003 by Mutuelles du Mans. This
financial product returns 2.5 % for sure every year and, when lucky, additional 5 %, 10 % or
20 % (see details in the Scilab code below). We want to test its success to the public by
comparison with a safe product returning a fixed rate every year (anchor).
Question 13 The values for MMmax are given below. Show that its mean return is slightly
more than 3.5% Draw the evaluation of this product as function of the anchor for an investor
evaluating prospects according to Cumulative Prospect Theory (CPT investor, in short).
Observe that any safe product with return more than 3.3% is prefered to the risky MMmax.
Conclude that a CPT investor is less encline to invest in MMmax than in safe product,
compared to a risk-neutral investor.
//
lotery_MMmax=[1025 1075 1125 1225 ; // return for 1000 euros
0.81 0.171 0.0171 0.0019] ; // probabilities
// Compte d'\'epargne MMmax launched in November 2003 by
// Mutuelles du Mans
disp("=======================================");
disp("This is the MMmax lotery for an investment of 1000 euros")
disp(lotery_MMmax)
//=========================================================
function v=scaling(w)
v=(w-1000)/10; // converts from euros to percents
endfunction
function w=unscaling(v)
w=1000 + 10*v ; // converts from percents to euros
endfunction
function v=RN_eval(lotery,anchor)
// Risk Neutral evaluation in euros
v= sum(prod(lotery,'r')) - anchor ;
endfunction
//=========================================================
exec CPT.sci
mean_MMmax= RN_eval(lotery_MMmax,0) ;
mean_MMmax_percent=scaling(mean_MMmax);
disp("=======================================");
disp('The expected return of the MMmax lotery is '...
+string(mean_MMmax_percent) +'%');
//=========================================================
step=0.01 ;
anchors_percent=[3.0 : step : (mean_MMmax_percent+20*step) ];
anchors=unscaling(anchors_percent) ; // return for 1000 euros
CPT_Values=[];RN_Values=[];
// getf('CPT.sci')
for anchor=anchors
CPT_Values=[CPT_Values,CPT_eval(lotery_MMmax,anchor)];
RN_Values=[RN_Values,RN_eval(lotery_MMmax,anchor)];
end
xset('window',30)
xbasc(); plot2d(anchors_percent,...
[ 0*ones(anchors) ; CPT_Values ; RN_Values ]' );
xtitle('CPT and RN evaluation of MMmax ...
as function of the anchor','anchor (%)','')
legends([ 'Cumulative Prospect Theory (CPT)'; 'Risk Neutral (RN)' ] ,...
[2,3], 'ur' );
xstring(2.95,-1.5,["RN and CPT prefer" ; "MMax to safe"],0,0)
xstring(3.3,1.5,["RN prefers MMax to safe but not CPT"],30,1)
xstring(3.55,0.5,["RN and CPT prefer" ; "safe to MMax"],0,0)
//=========================================================
anchor=1033.37;
disp("for annual safe return anchor of " +string(scaling(anchor)) +"%, ...
the CPT evaluation is " +string(CPT_eval(lotery_MMmax,anchor)))
anchor=1033.38;
disp("for annual safe return anchor of " +string(scaling(anchor)) +"%, ...
the CPT evaluation is " +string(CPT_eval(lotery_MMmax,anchor)))
//
References
Rudiger Frey and Alexander J. McNeil. Var and expected shortfall in portfolios of
dependent credit risks: Conceptual and practical insights. Journal of Banking and Finance,
26:1317–1334, 2002.
C. Gollier. The Economics of Risk and Time. MIT Press, Cambridge, 2001.
Daniel Kahneman and Amos Tversky. Prospect theory: An analysis of decision under
risk. Econometrica, 47(2):263–292, 1979.
Marie Pfiffelmann and Patrick Roger. Les comptes d’épargne associés à des loteries:
approche comportementale et étude de cas. Banque & Marchés, septembre 2005.
Amos Tversky and Daniel Kahneman. Advances in prospect theory: Cumulative
representation of uncertainty. Journal of Risk and Uncertainty, 5(4):297–323, October
1992.
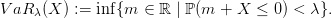
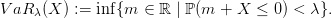
 describes a hazard situation where
describes a hazard situation where  are scalar. Let us be given a utility function
are scalar. Let us be given a utility function
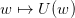 . The value of the lottery is the expectation of the utilities
. The value of the lottery is the expectation of the utilities  :
:
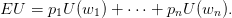
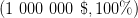 and
and
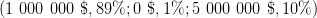 for different utility functions:
for different utility functions: 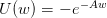 , A > 0;
, A > 0;
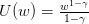 , γ > 0, γ ⁄= 1, w > 0.
, γ > 0, γ ⁄= 1, w > 0. and
and 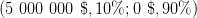 .
.
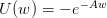 , A > 0. Compute the Arrow-Pratt coefficient of absolute risk
aversion
, A > 0. Compute the Arrow-Pratt coefficient of absolute risk
aversion 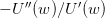 . Select a proper range of values for the parameter A. How do you
explain what you observe when the parameter A varies?
. Select a proper range of values for the parameter A. How do you
explain what you observe when the parameter A varies?
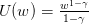 , γ > 0, γ ⁄= 1,
w > 0. Compute the Arrow-Pratt coefficient of relative risk aversion
, γ > 0, γ ⁄= 1,
w > 0. Compute the Arrow-Pratt coefficient of relative risk aversion 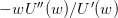 .
How do you explain what you observe when the parameter γ varies? Compare your results
with the one in the document Lettre à S. by the economist Laurent Denant-Boemont. Do you
agree with all his comments?
.
How do you explain what you observe when the parameter γ varies? Compare your results
with the one in the document Lettre à S. by the economist Laurent Denant-Boemont. Do you
agree with all his comments?
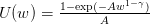 ,
1 > γ > 0, w > 0.
,
1 > γ > 0, w > 0.
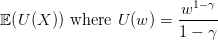
![1 1
U (w0(1 − π γ(𝜃 ))) = 𝔼 [U (w0X )] = -U (w0(1 − 𝜃)) + -U (w0 (1 + 𝜃))
2 2](risk_preferences22x.png)
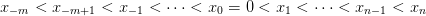
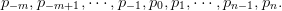
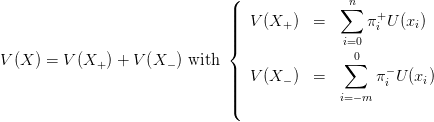
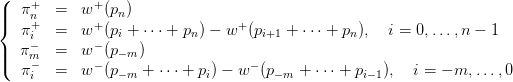

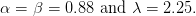
![+ --------pγ+--------- − ---------pγ−--------
w (p) = γ+ γ+ 1∕γ+ and w (p) = γ− γ− 1∕γ−
[p + (1 − p) ] [p + (1 − p) ]](risk_preferences30x.png)
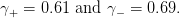
 1 − 𝜃
1 − 𝜃 gives:
gives: