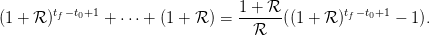Investing in bonds or in stock market?

Michel De Lara
(last modiﬁcation date: October 10, 2017)

Version pdf de ce document
Version sans bandeaux

1 A look at annual data from stock French market
2 Perception of the risk of stock market on diﬀerent investment durations
3 Perception of the risk of regular investment in stock market

1 A look at annual data from stock French market
1.1 Annual historical returns
1.2 Equivalent annual historical returns
1.3 Regular investment
1.4 Equivalent annual historical returns for yearly investment strategy
2 Perception of the risk of stock market on diﬀerent investment durations
2.1 Historical returns on ﬁxed investment duration
2.2 CPT evaluation of risky historical returns on ﬁxed investment durations
3 Perception of the risk of regular investment in stock market
3.1 Historical returns for regular investment in stock market
3.2 CPT evaluation of historical returns for regular investment in stock market

1 A look at annual data from stock French market

1.1 Annual historical returns

Here are data from http://www.euronext.com

Indice CAC40 Performance

Fin année Indice prix % Indice prix Rentabilité nette % Rentabilité nette

31/12/1987 1000,00 - 1000,00 -
30/12/1988 1573,94 57,39% 1606,82 60,68%
29/12/1989 2001,08 27,14% 2082,58 29,61%
28/12/1990 1517,93 -24,14% 1609,91 -22,70%
31/12/1991 1765,66 16,32% 1916,19 19,02%
31/12/1992 1857,78 5,22% 2060,31 7,52%
31/12/1993 2268,22 22,09% 2570,48 24,76%
30/12/1994 1881,15 -17,06% 2176,64 -15,32%
29/12/1995 1871,97 -0,49% 2213,92 1,71%
31/12/1996 2315,73 23,71% 2795,90 26,29%
31/12/1997 2998,91 29,50% 3684,87 31,80%
30/12/1998 3942,66 31,47% 4908,03 33,19%
30/12/1999 5958,32 51,12% 7515,81 53,13%
29/12/2000 5926,42 -0,54% 7550,48 0,46%
28/12/2001 4624,58 -21,97% 5975,25 -20,86%
31/12/2002 3063,91 -33,75% 4032,77 -32,51%
31/12/2003 3557,90 16,12% 4785,01 18,65%
31/12/2004 3821,16 7,40% 5268,31 10,10%
30/12/2005 4715,23 23,40% 6669,63 26,60%
29/12/2006 5541,76 17,53% 8061,85 20,87%

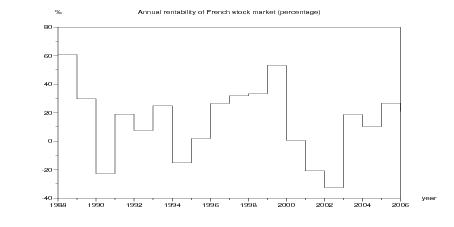
Question 1 Draw diﬀerent graphical representations of the historical annual rentability of French stock market (in percentage).

years=1988:2006 ;

cac40_perf_percent=[60.68 29.61 -22.70 19.02 7.52 ...
24.76 -15.32 1.71 26.29 31.80 33.19 53.13 0.46 -20.86 ...
-32.51 18.65 10.10 26.60 20.87] ;

xset('window',40) ; xbasc();
plot2d2(years,cac40_perf_percent);
xtitle('Annual rentability of French stock market (percentage)',...
'year','%')

xset('window',41) ; xbasc();
plot2d(sort(cac40_perf_percent));
xtitle('Sorted annual rentability of French stock market (percentage)')

xset('window',42) ; xbasc();
histplot((-40):20:70,cac40_perf_percent);

//

Figure 1: Annual rentability of French stock market (percentage)

1.2 Equivalent annual historical returns

Suppose that you choose an investment duration of T years. You invest at the beginning of any year between 1988 and 2006 − T + 1, and you compare the ﬁnal value with what an investment with safe return would have given on the same duration T. We shall call the return for which both are equivalent the historical equivalent annual rentability. Letting the year between 1988 and 2006 − T + 1 vary, we obtain, for each investment duration T, an array of historical equivalent annual rentabilities.

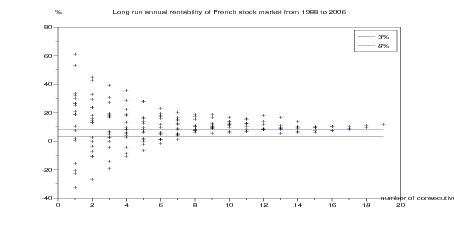
Question 2 Compute the historical equivalent annual rentabilities of French stock market over 1,2, …, 19 consecutive years. Draw a graphic with the number of consecutive years as horizontal axis and the historical rentabilities as vertical axis.

t0=years(1);
tf=years($);
duration=1:(tf-t0+1);
cac40_equi_returns=list();
// cac40_equi_returns(k) is the vector of
// equivalent annual returns over k consecutive years

xset('window',43) ; xbasc() ;
for i=duration;
  loc_vec=[];
  for j=1:(tf-t0-i+2);
loc=cumprod(1 + 0.01 *cac40_perf_percent(j:(j+i-1)));
loc_vec=[loc_vec,(loc($))^{1/i}-1];
  end
  plot2d(i*ones(loc_vec),100*loc_vec,style=-1)
  cac40_equi_returns(i)=100*loc_vec;
end
xtitle('Long run annual rentability of French stock market from '...
+string(t0) +' to ' +string(tf) ,...
   'nb consecutive years','%')
plot2d([0 duration], ones([0 duration]') * [3 8] ); // ,style=[2 3]);
legends([ '3%'; '8%' ] , [1,2], 'ur' );

//

Figure 2: Historical equivalent annual rentabilities (percentage) of French stock market as function of the duration of investment

1.3 Regular investment

Consider t_f − t₀ + 1 periods t₀, t₀ + 1, …, t_f (which will be years in this context). Investing a unitary amount of money at the beginning of period t is supposed to return 1 + ℛ(t) at the beginning of period t + 1. Thus, if your planning strategy is to invest ℐ(t) at the beginning of every period t ∈{t₀,t₀ + 1,…,t_f}, you can evaluate your fortune at the horizon T = t_f + 1.

function [capital,plus_values]=reg_invest(invest_tab,return_tab)
periods=cumsum(ones(invest_tab)) ;
cumul_invest=cumsum(invest_tab);
// invest_tab : array of regular investment amounts
// return_tab : array of returns
// capital : at last period 1+periods($)
capital=[];
plus_values=[];
for t=periods
  capital_loc= ( capital($) + invest_tab(t) ) * (1+return_tab(t))  ;
  capital=[capital capital_loc];
  plus_values=[plus_values capital_loc-cumul_invest(t) ] ;
end
endfunction

//

Question 3 Suppose now that the same strategy is applied with a ﬁxed return ℛ, giving fortune at the horizon T = t_f + 1

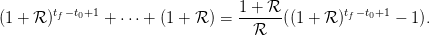
1 + ℛ (1 + ℛ )tf−t0+1 + ⋅⋅⋅ + (1 + ℛ ) =------((1 + ℛ )tf−t0+1 − 1). ℛ

Which is the ﬁxed rate ℛ_s which gives the same ﬁnal fortune than with a time-varying return ℛ(⋅)?

function retour=equi_return(nb_periods,fortune)
function y=f(rate)
y=( 1 + (1 ./rate) ) .* ( (1+rate).^(nb_periods) -1 ) - fortune ;
endfunction
retour=fsolve(0.03,f)
endfunction

//

1.4 Equivalent annual historical returns for yearly investment strategy

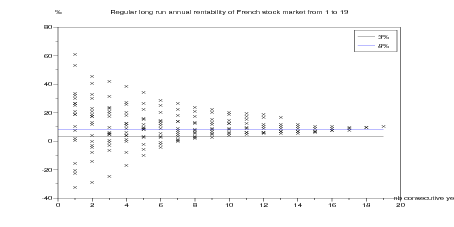
Question 4 Suppose you invest a unitary amount of money at the beginning of every year in the stock market. Evaluate the equivalent ﬁxed rates, on diﬀerent horizons, of the strategy consisting of investing the same amount every year on the stock market.

t0=years(1);
tf=years($);
duration=1:(tf-t0+1);
cac40_equi_yearly_returns=list();
// cac40_equi_returns(i) is the vector of
// equivalent annual returns for regular annual investment
// over i consecutive years

xset('window',63) ; xbasc() ;
for i=duration;
  loc_vec=[];
  for j=1:(tf-t0-i+2);
// loop when the investment horizon i is fixed
return_tab=0.01*cac40_perf_percent(j:(j+i-1));
invest_tab=ones(return_tab);
// unitary amount of regular annual investment
[capital,plus_values]=reg_invest(invest_tab,return_tab);
nb_periods=sum(ones(invest_tab));
fortune=capital($);
retour=equi_return(nb_periods,fortune);
loc_vec=[loc_vec,retour];
  end
  plot2d(i*ones(loc_vec),100*loc_vec,style=-2);
  cac40_equi_yearly_returns(i)=100*loc_vec;
end
xtitle('Yearly investment in French stock market from '...
+string(t0) +' to ' +string(tf) ...
   +': annual rentability',...
'nb consecutive years','%')
plot2d([0 duration], ones([0 duration]') * [3 8] );
legends([ '3%'; '8%' ] , [1,2], 'ur' );

//

Figure 3: Historical equivalent annual rentabilities (percentage) of French stock market as function of the duration of investment in case of yearly investment

2 Perception of the risk of stock market on diﬀerent investment durations

2.1 Historical returns on ﬁxed investment duration

Suppose that you choose an investment duration of T years and an initial capital of 1 000 euros. Consider that the investment may have started at the beginning of any year between 1988 and 2006 − T + 1. Letting the year between 1988 and 2006 − T + 1 vary, we obtain, for each investment duration T, an array of historical returns. For T = 1 year, we obtain 2006 − 1988 + 1 = 19 historical returns; for T = 2 years, 18 years; …; for T = 19, only 1 historical return.

Question 5 Draw graphics for T = 1, T = 2, T = 10 with years between 0 and T in abcisse and a straight line joining 1 000 euros to the diﬀerent historical returns. The straight lines ignore the variability during the investment period to focus only on the ﬁnal return.

t0=years(1);
tf=years($);
duration=1:(tf-t0+1);
cac40_hist_returns=list();
// cac40_hist_returns(i) is the vector of
// returns over i consecutive years for 1000 euros investment

for i=duration;
  loc_vec=[];
  for j=1:(tf-t0-i+2);
loc=1000*cumprod(1 + 0.01 *cac40_perf_percent(j:(j+i-1)));
// for 1000 euros investment
loc_vec=[loc_vec,loc($)];
  end
  cac40_hist_returns(i)=loc_vec;
end

for i=[1 2 5 8 12]
  xset('window',70+i) ; xbasc() ;
  plot2d([0 i],[1000*ones(cac40_hist_returns(i)')...
cac40_hist_returns(i)' ]')
  xtitle('Stock market historical returns after ' +string(i) +...
   ' investment years','years')
xpoly([0 i],[1000 1000*(1+.03)^i] ,"lines",0)
  p=get("hdl"); //get handle on current entity (here the polyline entity)
  p.thickness=6;
  p.line_style=5;
end

//

(a) 1 year

(b) 2 years

(d) 12 years

Figure 4: French stock market historical returns for same initial investment under diﬀerent sequences of consecutive years

2.2 CPT evaluation of risky historical returns on ﬁxed investment durations

For each number T of consecutive years, one has an array of historical returns, supposed to be the values taken by a prospect X(T) with equal probabilities. We shall evaluate X(T) with the so called Cumulative prospect theory or CPT (see [KT79, TK92]), presented in Risk and Decision.

Question 6 Draw the evaluation of the prospect X(T) as a function of investment duration T. Where do you see that the stock market is not chosen if its returns are only perceived on an annual basis? What is the investment time needed to prefer stock market to a safe investment between 2% and 3% [BT95]?

// exec Code/CPT.sci

anchors_percent=0:0.25:10 ;
Values=zeros(anchors_percent'*duration);

for i=duration;
values=cac40_hist_returns(i);
lotery=[ values ; (1/sum(ones(values)))*ones(values) ] ;
// deff('y=f(x)','y=CPT_eval(lotery,x)');
// indif_anch(i)=fsolve(3,f);
loc_Values=[];
for k=1:prod(size(anchors_percent));
anchor=1000* (1+0.01*anchors_percent(k))^i ;
  loc_Values=[loc_Values;CPT_eval(lotery,anchor)];
end
// Values(k,:)=loc_Values;
Values(:,i)=loc_Values;
end

xset('window',65) ; xbasc() ;
plot2d(duration,[zeros(duration)' Values([1 9 13],:)']);
xtitle('CPT evaluation of historical stock market returns', ...
'investment length (years)');
legends([ 'anchor '+string(anchors_percent(1))+'%'; ...
'anchor '+string(anchors_percent(9))+'%' ; ...
  'anchor '+string(anchors_percent(13))+'%'],...
[2 3 4], 'ul');

[lhs,ind]=mini(abs(Values),"r");
CPT_indif=anchors_percent(ind);

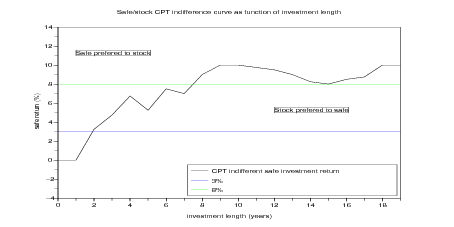
xset('window',66) ;  xbasc() ;
plot2d([0 duration], ...
   [ [0 CPT_indif]' ones([0 duration]') * [3 8] ],...
rect=[0,-4,duration($),14]);
legends([ 'CPT indifferent safe investment return' ; '3%'; '8%' ] , ...
[1,2,3], 'lr' );
xstring(1,11,["Safe prefered to stock"],0,1)
xstring(12,5,["Stock prefered to safe"],0,1)
xtitle('Safe/stock CPT indifference curve ...
as function of investment length','investment length (years)',...
'safe return (%)');

//

Figure 5: CPT indiﬀerence curve between safe or historical stock market rentability as function of investment length. For instance, a CPT investor is indiﬀerent between investing 5 years in stock markets or 5 years at 6% safe return; a CPT investor prefers investing 10 years in stock markets than 10 years at 9% safe return.

3 Perception of the risk of regular investment in stock market

3.1 Historical returns for regular investment in stock market

Suppose that you choose an investment duration of T years and a regular investment of 1 000 euros at the beginning of each year. Consider that the investment may have started at the beginning of any year between 1988 and 2006 − T + 1. Letting the year between 1988 and 2006 − T + 1 vary, we obtain, for each investment duration T, an array of historical returns. For T = 1 year, we obtain 2006 − 1988 + 1 = 19 historical returns; for T = 2 years, 18 years; …; for T = 19, only 1 historical return.

Question 7 Draw graphics for T = 1, T = 2, T = 10 with years between 0 and T in abcisse and a straight line joining 1 000 euros to the diﬀerent historical returns. The straight lines ignore the variability during the investment period to focus only on the ﬁnal return.

t0=years(1);
tf=years($);
duration=1:(tf-t0+1);
cac40_yearly_invest_returns=list();
// cac40_yearly_invest_returns(i) is the vector of
// returns for regular annual investment
// over i consecutive years

for i=duration;
  loc_vec=[];
  for j=1:(tf-t0-i+2);
// loop when the investment horizon i is fixed
return_tab=0.01*cac40_perf_percent(j:(j+i-1));
invest_tab=ones(return_tab);
// unitary amount of regular annual investment
[capital,plus_values]=reg_invest(invest_tab,return_tab);
loc_vec=[loc_vec,capital($)];
  end
  cac40_yearly_invest_returns(i)=1000*loc_vec;
   // for 1000 euros annual investment
end

for i=[1 2 5 8 12]
  xset('window',90+i) ; xbasc() ;
  plot2d([0 i],[1000*ones(cac40_yearly_invest_returns(i)')  ...
cac40_yearly_invest_returns(i)' ]')
  xtitle('Regular investment returns after ' +string(i) +...
   ' investment years','years')
  return_tab=0.03*ones(1:i);
  // investment of length i
  invest_tab=ones(return_tab);
  // unitary amount of regular annual investment
  [capital,plus_values]=reg_invest(invest_tab,return_tab);
xpoly([0 i],[1000 1000*capital($)] ,"lines",0)
  p=get("hdl"); //get handle on current entity (here the polyline entity)
  p.thickness=6;
  p.line_style=5;
end

//

(a) 1 year

(b) 2 years

(d) 12 years

Figure 6: French stock market historical returns for same initial investment under diﬀerent sequences of consecutive years

3.2 CPT evaluation of historical returns for regular investment in stock market

Suppose that you choose an investment duration of T years and a regular investment of 1 000 euros at the beginning of each year. For each number T of consecutive years, one has an array of historical returns, supposed to be the values taken by a prospect Y (T) with equal probabilities. We shall evaluate X(T) with the CPT.

Question 8 Draw the evaluation of the prospect Y (T) as a function of investment duration T. Where do you see that the stock market is not chosen if its returns are only perceived on an annual basis? What is the investment time needed to prefer stock market to a safe investment between 2% and 3% [BT95]?

Figure 7: CPT indiﬀerence curve between safe or historical stock market rentability as function of investment length for yearly investment strategy. For instance, a CPT yearly investor is indiﬀerent between investing 4 years in stock markets or 4 years at 5% safe return; a CPT investor prefers investing 10 years in stock markets than 10 years at 8% safe return.

// exec Code/CPT.sci

anchors_percent=0:0.25:10 ;
Values=zeros(anchors_percent'*duration);

for i=duration;
values=cac40_yearly_invest_returns(i);
lotery=[ values ; (1/sum(ones(values)))*ones(values) ] ;
// deff('y=f(x)','y=CPT_eval(lotery,x)');
// indif_anch(i)=fsolve(3,f);
loc_Values=[];
for k=1:prod(size(anchors_percent));
  return_tab=0.01*anchors_percent(k)*ones(1:i);
  // investment of duration i
  invest_tab=ones(return_tab);
  // unitary amount of regular yearly investment
  [capital,plus_values]=reg_invest(invest_tab,return_tab);
  anchor=1000* capital($);
  // for 1000 euros annual investment
  loc_Values=[loc_Values;CPT_eval(lotery,anchor)];
end
// Values(k,:)=loc_Values;
Values(:,i)=loc_Values;
end

xset('window',105) ; xbasc() ;
plot2d(duration,[zeros(duration)' Values([1 9 13],:)']);
xtitle('CPT evaluation of stock market returns ...
   with yearly investment', ...
'investment duration (years)');
legends([ 'anchor '+string(anchors_percent(1))+'%'; ...
'anchor '+string(anchors_percent(9))+'%' ; ...
  'anchor '+string(anchors_percent(13))+'%'],...
[2 3 4], 'ul');

[lhs,ind]=mini(abs(Values),"r");
CPT_indif_yearly=anchors_percent(ind);

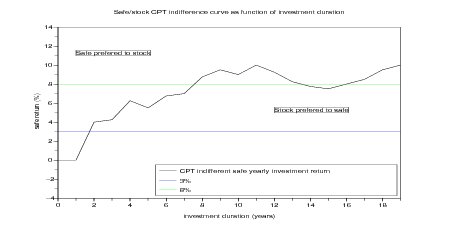
xset('window',106) ;  xbasc() ;
plot2d([0 duration], ...
   [ [0 CPT_indif_yearly]' ones([0 duration]') * [3 8] ],...
rect=[0,-4,duration($),14]);
legends([ 'CPT indifferent safe yearly investment return' ; '3%'; '8%' ] , ...
[1,2,3], 'lr' );
xstring(1,11,["Safe prefered to stock"],0,1)
xstring(12,5,["Stock prefered to safe"],0,1)
xtitle('Safe/stock CPT indifference curve ...
as function of investment duration','investment duration (years)',...
'safe return (%)');

xset('window',166) ;  xbasc() ;
plot2d([0 duration], ...
   [ [0 CPT_indif]' [0 CPT_indif_yearly]' ...
ones([0 duration]') * [3 8] ],...
rect=[0,-4,duration($),14]);
legends([ 'CPT indifferent safe investment return' ; ...
  'CPT indifferent safe yearly investment return' ; '3%'; '8%' ] , ...
[1,2,3,4], 'lr' );
xtitle('Safe/stock CPT indifference curves ...
as function of investment duration','investment duration (years)',...
'safe return (%)');

//

References

[BT95] Shlomo Benartzi and Richard H Thaler. Myopic loss aversion and the equity premium puzzle. The Quarterly Journal of Economics, 110(1):73–92, February 1995. available at http://ideas.repec.org/a/tpr/qjecon/v110y1995i1p73-92.html.

[KT79] D. Kahneman and A. Tversky. Prospect theory: an analysis of decision under risk. Econometrica, 47:263–291, 1979.

[TK92] Amos Tversky and Daniel Kahneman. Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5(4):297–323, October 1992. available at http://ideas.repec.org/a/kap/jrisku/v5y1992i4p297-323.html.