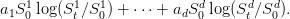Contents
Préliminaires
- Ecrire une fonction Scilab qui calcule la moyenne empirique (moyenne, la variance
empirique Variance empirique d’un tableau de nombre.
Vérifiez qu’elles coïncident avec les fonctions prédéfinies de Scilab : mean, variance.
- Ecrire une fonction permettant de simuler un vecteur consituer de variables aléatoires
gaussiennes centrées réduites indépendantes.
Tracer l’histogramme du vecteur obtenu et verifier qu’il correspond bien à la loi gaussienne
centrée réduite.
Cette fonction existe dans Scilab (x=rand(1,n,’’gauss’’)).
- On cherche à calculer par simulation 𝔼(eβG) où G est une gaussienne centrée réduite. On
rappelle que 𝔼(eβG) = exp(β2∕2).
Calculer par simulation 𝔼(eβG) pour β = 2, 4, 6, 8, 10…. Précisez à chaque fois une intervalle
de confiance. Pour quelles valeurs de β peut on utiliser une méthode de Monte-Carlo
?
Le modèle de Black et Scholes
On considère le modèle de Black et Scholes :
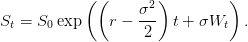
On supposera dans la suite que S0 = 100, σ = 0.3 (volatilité annuelle) et r = 0.05 (taux d’intérêt
exponentiel annuel).
- Tracer l’histogramme de la loi de ST , pour T = 1, σ = 0.3 (volatilité annuelle) et r = 0.05
(taux d’intérêt exponentiel annuel).
- On cherche à calculer le prix d’un call de strike K = 100. Calculer ce prix par une méthode
de Monte-Carlo avec un nombre de tirages égaux à N = 1000,1000,10000. On précisera
l’intervalle de confiance.
- On va chercher à utiliser la variable aléatoire ST comme une variable de contrôle. Vérifiez
que 𝔼(ST ) = ert (pourquoi ?).
Ecrire un programme qui utilise ST comme variable de contrôle. Comparer la
précision de cette méthode avec la précédente suivant les valeur relative de K et
S0.
Se convaincre que l’on a ainsi ramené le calcul du call à un calcul de put.
- On se place dans la cas d’un call de strike K grand devant S0. Montrer par simulation que la
précision relative du calcul au fur et à mesure que K∕S0 décroit. On prendra S0 = 100 et
K = 100, 150, 200, 250. Que se passe t’il pour K = 400 ?
- Montrer en utilisant le théorème de Girsanov que :
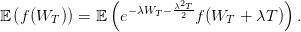
On se place dans le cas du call avec S0 = 100 et K = 150. Proposer une valeur de λ
permettant de réduire la variance de la simulation.
Partie 2 : Modèle de Panier
On s’intéresse à un modèle de panier constitué à partir de d actifs. On suppose que chacun de
ces d actifs de prix Sti suit un modèle de black et Scholes guidé par un mouvement
Wti :
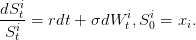
On prendra dans les applications numériques xi = 100 et d = 10.
Pour déterminer complètement le modèle on doit spécifier les corrélation entre les mouvements
browniens. Pour cela on suppose que :
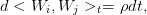
ρ étant une constante donnée que l’on prendra égale à 0.5 dans les simulations.
- Calculer la matrice de corrélation du vecteur (WT 1,…,W
T d). Montrer (à l’aide de
MatLab) qu’elle est définie positive.
- Proposer une méthode de simulation pour le vecteur (WT 1,…,W
T d) et (S
T 1,…,S
T d).
- On s’intéresse maintenant au calcul du prix d’un call sur un indice de prix It donnée
par
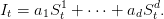
On prendra dans les applications numériques a1 =  = ad = 1∕d. Calculer par
simulation la valeur du call de payoff à l’instant T
= ad = 1∕d. Calculer par
simulation la valeur du call de payoff à l’instant T
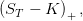
et estimer l’erreur commise dans le cas où K = I0.
- Montrer une relation d’arbitrage call-put et montrer que l’on peut l’utiliser pour mettre
en oeuvre une technique de réduction de variance.
- En utilisant le théorème de Girsanov pour les d mouvement brownien proposer une
technique de réduction de variance dans le cas où I0 est petit devant K.
- En supposant que r et σ tendent vers 0 monter que l’on peut approximer log(It∕I0)
par :
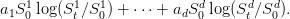
En déduire une variable de contrôle pour le calcul du prix du call. Évaluer par
simulation le gain de la méthode.
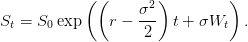
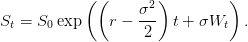
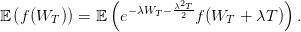
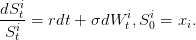
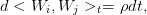
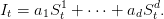
 = ad = 1∕d. Calculer par
simulation la valeur du call de payoff à l’instant T
= ad = 1∕d. Calculer par
simulation la valeur du call de payoff à l’instant T