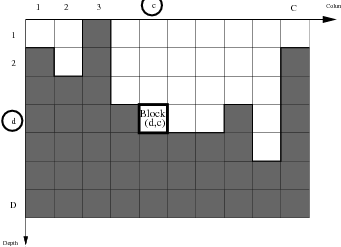
Open pit mines are generally designed with the help of so-called block models, or resource models. These latter represent the material inside the pit using millions of blocks with given shape. Open pit mines extraction is submitted to physical restrictions: only blocks at the surface may be extracted; a block cannot be extracted if the slope made with one of its neighbors is too high, due to geotechnical constraints on mine wall slopes.
In essence, exploiting an open pit mine can be seen as selecting an admissible extraction sequence of blocks where, by admissible, we mean that the above physical restrictions are satisfied. Among all admissible extraction sequences, of particular economic interest are those which are the more profitable.
For simplicity, we shall consider a two-dimensional mine [1] as in Fig. 1. Each block is a two-dimensional rectangle identified by its vertical position d ∈{1,…,D} (d for depth) and by its horizontal position c ∈{1,…,C} (c for column).
We assume that blocks are extracted sequentially under the following hypothesis [2, 1]:
Denote discrete time by t = 0, 1,…,T, where an upper bound for the number of extraction steps is the number C × D of blocks (it is in fact strictly lower due to slope constraints). At time t, the state of the mine is a profile
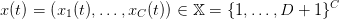
where xc(t) ∈{1,…,D + 1} is the vertical position of the top block with horizontal position c ∈{1,…,C} (see Fig. 1). The initial profile is x(0) = (1, 1,…, 1) while the mine is totally exhausted in state x = (D + 1,D + 1,…,D + 1).
An admissible profile is one that respects local angular constraints at each point, due to physical requirements. A state x = (x1,…,xC) is said to be admissible if the geotechnical slope constraints are respected in the sense that
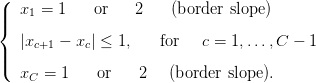 | (1) |
Denote by 𝔸 ⊂{1,…,D + 1}C the set of admissible states satisfying the above slope constraints (1).
A decision is the selection of a column in ℂ = {1,…,C}, the top block of which will be extracted. A decision may also be the retirement option, that we shall identify with an additional fictituous column denoted ∞. Thus, a decision u is an element of the set ℂ = ℂ ∪{∞} = {1,…,C,∞}.
At time t, if a column u(t) ∈{1,…,C} is chosen at the surface of the open pit mine, the
corresponding block is extracted and the profile x(t) =  x1(t),…,xC(t)
x1(t),…,xC(t) becomes
becomes
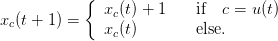 |
In case of retirement option u(t) = ∞, then x(t + 1) = x(t) and the profile does not change. In other words, the dynamics is given by x(t + 1) = DYN(x,u) where
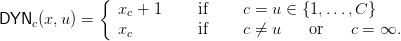 | (2) |
Indeed, the top block of column c is no longer at depth xc(t) but at xc(t) + 1, while all other top blocks remain.
Starting from state x = (2, 3, 1, 4, 3) in Figure 2 and applying control u = 3, one obtains the following state (2, 3, 2, 4, 3) as in Figure 3.
Not all decisions u(t) = c are possible either because there are no blocks left in column c (xc = D + 1) or because of slope constraints.
When in state x ∈ 𝔸, the decision u ∈ℂ is admissible if the future profile DYN(x,u) ∈ 𝔸, namely if it satisfies the geotechnical slope constraints. This may easily be transformed into a condition u ∈ 𝔹(x), where
 | (3) |
The open pit mine optimal scheduling problem consists in finding a path of admissible blocks which
maximizes an intertemporal discounted extraction profit. It is assumed that the value of blocks differs
in depth and column because richness of the mine is not uniform among the zones as well as costs of
extraction. The profit model states that each block has an economic value Rent(d,c) ∈ ℝ, supposed to
be known.1
By convention Rent(d,∞) = 0 when the retirement option is selected. Selecting a column
u(t) ∈ ℂ at the surface of the open pit mine, and extracting the corresponding
block2
at depth xu(t)(t) yields the value Rent xu(t)(t),u(t)
xu(t)(t),u(t) . With discount rate rf ≥ 0 and discount factor
0 ≤
. With discount rate rf ≥ 0 and discount factor
0 ≤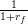 ≤ 1, the optimization problem is sup u(⋅) ∑
t=0+∞(
≤ 1, the optimization problem is sup u(⋅) ∑
t=0+∞(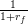 )tRent
)tRent x
u(t)(t),u(t)
x
u(t)(t),u(t) . Notice that
the sum is in fact finite, bounded above by the number T − 1 of blocks. Thus, we shall rather
consider3
. Notice that
the sum is in fact finite, bounded above by the number T − 1 of blocks. Thus, we shall rather
consider3
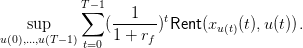 | (4) |
The maximization problem (4) may theoretically be solved by dynamic programming. The value function 𝒱(t,x) solves 𝒱(T,x) = 0 and
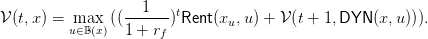 | (5) |
However, due to numerical considerations (curse of dimensionality), we shall have to introduce a new, and more parcimonious, state before applying the dynamic programming algorithm.
To give a flavor of the complexity of the problem, notice that 4 columns (C = 4) each consisting of nine blocks (D = 9) give 10 000 states (𝕏♯ = 104), while this raises to 1020 000 if we assume that the surface consists of 100 × 100 columns (C = 10 000) with ninety-nine blocks (D = 99) .
However, the set 𝔸 of acceptable states has a cardinal 𝔸♯ which is generally much smaller than
𝕏♯. To see this, let us introduce the mapping x = (x
1,…,xC)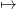 φ(x) = (x1,x2 − x1,…,xC − xC−1).
Let x ∈ 𝔸 and y = φ(x). Since x satisfies the admissibility condition (1), y necessarily satisfies
y1 ∈{1, 2} and sup c=2,…,C
φ(x) = (x1,x2 − x1,…,xC − xC−1).
Let x ∈ 𝔸 and y = φ(x). Since x satisfies the admissibility condition (1), y necessarily satisfies
y1 ∈{1, 2} and sup c=2,…,C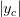 ≤ 1. Hence, card(𝔸) ≤ 2 × 3C−1 and the dynamic programming
algorithm will be released with the new state y = (y1,…,yC) ∈{1, 2}×{−1, 0, 1}C−1 corresponding
to the increments of the state x. Table 2 provides some figures.
≤ 1. Hence, card(𝔸) ≤ 2 × 3C−1 and the dynamic programming
algorithm will be released with the new state y = (y1,…,yC) ∈{1, 2}×{−1, 0, 1}C−1 corresponding
to the increments of the state x. Table 2 provides some figures.
| C | D | 𝕏♯ | 𝔸♯ | 𝔸♯∕𝕏♯ |
| 4 | 9 | 104 | ≤ 270 | ≤ 3 % |
| 10 000 | 99 | 1020 000 | ≤ 2 × 1010 000 | 2×≤ 10−10 000 |
The dynamic programming algorithm will be released with the new state
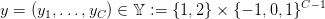 | (6) |
corresponding to the increments of the state x given by the inverse mapping
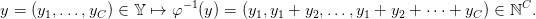 | (7) |
By construction, x = φ−1(y) always satisfies the slope constraints (1). However, it does not always correspond to a mine profile state. Indeed, some y ∈ 𝕐 give x = φ−1(y) ⁄∈ 𝕏 = {1,…,D + 1}C: for instance y = (1,−1,−1,…,−1) yields x = (1, 0,−1,−2,…,C − 2).
The dynamics (x,u)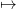 DYN(x,u) now becomes (y,u)
DYN(x,u) now becomes (y,u)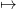 G(y,u) = φ
G(y,u) = φ DYN(φ−1(y),u)
DYN(φ−1(y),u) :
:
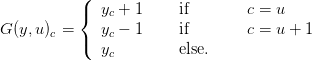 | (8) |
The new state set 𝕐 is a product space: we shall label its elements with integers. Let Q ∈{−1, 0, 1, 2,…} be the unique integer such that
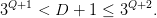 | (9) |
Consider the following labelling mapping4
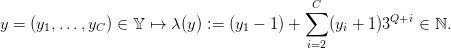 | (10) |
The inverse mapping of λ is given as follows. Any integer z ∈{0, 1,…, 3Q+C+1} may be decomposed in the basis {1, 3Q+2,…, 3Q+C} as
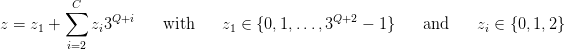 | (11) |
for i = 2,…,C. Thus (y1,…,yC) = λ−1(z) is given by y
1 = z1 + 1 ∈{1,…, 3Q+2} and
yi = zi − 1 ∈{−1, 0, 1} for i = 2,…,C. Denote by ℤa ⊂{0, 1,…, 3Q+C+1} those z to which
corresponds an admissible state x = φ−1 λ−1(z)
λ−1(z) ∈ 𝔸.
∈ 𝔸.
The dynamics (8) is translated in
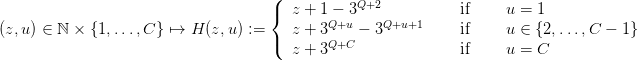 | (12) |
because of the expression (11) for z.
Let z ∈ ℤa. Of course, z′ = H(z,u) corresponds to an admissible state (z′∈ ℤa) if and only if
u is admissible for the state x = φ−1 λ−1(z)
λ−1(z) ∈ 𝔸, property that we shall denote by
u ∈ 𝕌a(z) ⊂{1,…,C}.
∈ 𝔸, property that we shall denote by
u ∈ 𝕌a(z) ⊂{1,…,C}.
Copy the file "marvin_7440_valores.txt" in your local directory. Then, create a file "data.sce" in your local directory containing the following code.
The so called value of the mine is 𝒱(0,x(0)) given by (4).
Question 1 Rearrange the elements of the matrix Rent(d,c) and deduce an upper bound for the value of the mine.
Copy the following code in a file "mine_DP_label.sce"
Copy the following code in a file "mine_DP_algorithm.sce"
Copy the following code in a file "mine_visualize.sce"
Copy the following code in a file "mine_DP_trajectories.sce"
Question 2 Copy the following code in a file "mine_DP.sce", then execute it. Change the economic model and the discount rate.
[1] M. De Lara and L. Doyen. Sustainable Management of Natural Resources. Mathematical Models and Methods. Springer-Verlag, Berlin, 2008.
[2] G.C. Goodwin, M.M. Seron, R.H. Middleton, M. Zhang, B.F. Hennessy, P.M. Stone, and M. Menabde. Receding horizon control applied to optimal mine planning. Automatica, 42(8):1337–1342, 2006.