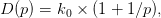
On étudie, en économie, un marché correspondant à un produit donné P. On connaît, pour P, la courbe de demande de l’ensemble des consommateurs en fonction du prix de vente, ainsi que la courbe d’offre de la part des producteurs en fonction du prix d’achat.
La courbe de demande est la suivante :
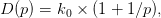 | (1) |
et la courbe d’offre est
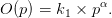 | (2) |
Les allures de ces courbes sont représentées sur les graphiques 1 et 2.
Question 1 Trouver le prix d’équilibre p⋆ du produit P sur le marché étudié. On prendra
k0 = 10, k1 = 150, et α = 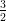 .
.
Voici un petit exemple illustrant ce qu’est la programmation linéaire. Un boulanger fabrique de la brioche et du pain viennois, désignés respectivement par X et Y . Il dispose pour cela de farine A en quantité a, de beurre B en quantité b et de sucre C en quantité c.
On suppose la linéarité de la production : x unités de X et y unités de Y exigent uA = 5x + 4y unités de A, uB = x + 2y unités de B, et uC = 3x + 2y unités de C.
La matrice M suivante résume les quantités de ressources nécessaires pour produire une unité de X ou de Y :
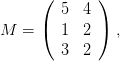
et
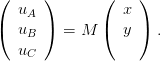
La limitation des ressources se traduit donc par les contraintes
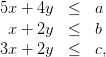
avec a = 80, b = 24, c = 36.
À ces trois contraintes, on peut rajouter les deux contraintes
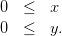
Enfin on suppose que le boulanger vend sa brioche X à un prix p et son pain brioché à un prix q, que l’on supposera tous deux indépendants de la quantité vendue, et on considère qu’il vend tout ce qu’il produit. On prendra p = 40 et q = 50.
Le boulanger veut maximiser son chiffre d’affaire C = px + qy, tout en étant contraint de
n’utiliser que ce qu’il a en stock ; il est donc confronté au problème suivant :
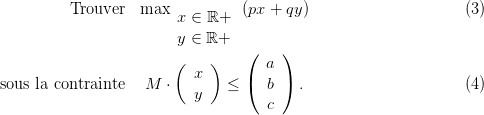
Question 2 En utilisant la fonction linpro de Scilab, résoudre le problème de notre boulanger.
Question 3 Quel sont les constituants limitants ? Quelles sont leurs valorisations marginales respectives ?
On modélise simplement une poutre, soumise à un chargement uniforme, par une succession de 2N + 1 barres rectilignes Bi de longueur r, reliées entre elles par des ressorts Ri exercant un couple de torsion −ki𝜃i. Pour modéliser le chargement, on suppose qu’une masse ponctuelle m est disposée sur chaque noeuds Pi, entre les barres Bi−1 et Bi. Les extrémités de la poutre sont libres.
On suppose le nombre de barres impair, et la symétrie du modèle par rapport à l’axe δ (figure 3).
Le détail du paramètrage est précisé sur la figure 4.
L’énergie du ressort Ri est
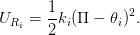
On supposera de plus que la masse étant relativement faible par rapport aux raideurs des couples de torsion, on peut se placer dans l’approximation des petits angles pour les αi pour i ∈{0…N}.
Question 4 En utilisant la fonction quapro de Scilab, déterminer la position de la poutre après chargement, i.e. les αi pour i ∈{0…N}.
On prendra :
On considère le problème suivant :
Un homme de masse m saute dans un gouffre. Il est relié à deux élastiques E1 et E2, de raideurs respectives k1, k2, et de longueurs à vide l1, l2. Les points d’ancrage des élastique sont diamètralement opposés et distants de L.
On suppose le goufre suffisamment profond (pas de borne max en y), on considère que le problème est plan, et on étudie la position d’équilibre de notre cascadeur.
On prendra :
Question 5 En utilisant la fonction optim de Scilab, déterminer la position d’équilibre de notre homme.