Contents
1 Problem data
We consider a dam manager intenting to maximize the intertemporal payoff obtained by selling
power produced by water releases, when the water inflows (rain, outflows from upper dams) are
random. However, the manager must also respect a minimal volume during the Summer months for
tourism reasons.
1.1 Dam dynamics
We model the dynamics of the water volume in a dam by
with
- time t ∈𝕋 := {t0,…,T} is discrete (such as days), and t denotes the beginning of the
period [t,t + 1[,
- S(t) volume (stock) of water at the beginning of period [t,t + 1[, belonging to the
discrete set
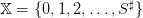 , made of water volumes, where
, made of water volumes, where 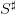 is the maximum
dam volume,
is the maximum
dam volume,
- a(t) inflow water volume (rain, etc.) during [t,t+1[, belonging to
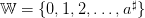
- decision-hazard: a(t) is not available at the beginning of period [t,t + 1[
- q(t) turbined outflow volume during [t,t + 1[, decided at the beginning of period
[t,t + 1[, supposed to depend on S(t) but not on a(t), belonging to the discrete set
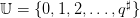 , where q♯ is the maximum which can be turbined by time unit
(and produce electricity),
, where q♯ is the maximum which can be turbined by time unit
(and produce electricity),
![s(t) = [S (t) − q(t) + a(t) − S ♯]
+](dam_viability5x.png) the spilled volume
the spilled volume
The dam manager is supposed to make a decision, here turbining q(t) at time t, before knowing
the water input a(t). Such a case is called decision-hazard. The constraint on the water turbine q(t)
is
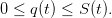 | (1) |
A scenario is a sequence of uncertainties:
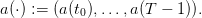 | (2) |
1.2 Criterion: intertemporal payoff
The manager original problem is one of payoff maximization where turbining one unit of water has
unitary price p(t). On the period from t0 to T, the payoffs sum up to
 | (3) |
where
1.3 Constraint: minimal volume during the Summer months
For “tourism” reasons, the following constraint is imposed
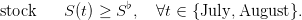
In what follows, we shall be more specific about the sense with which this constraint has to be
satisfied, namely in probability.
1.4 Water turbined strategy
A strategy Rule : 𝕋 × 𝕏 → 𝕌 assigns a water turbined 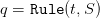 to any state S of dam stock
volume and to any decision period t ∈ 𝕋. Once given, we obtain uncertain volume trajectories
to any state S of dam stock
volume and to any decision period t ∈ 𝕋. Once given, we obtain uncertain volume trajectories
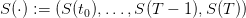 and turbined trajectories
and turbined trajectories 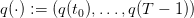 produced by the “closed-loop” dynamics
produced by the “closed-loop” dynamics
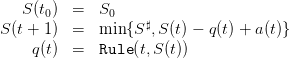 | (5) |
and function of the scenario a(⋅). Thus, in the end, we obtain an uncertain payoff
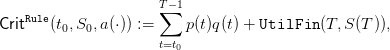 | (6) |
where 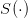 and
and 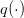 are given by (5).
are given by (5).
1.5 Probabilistic model on water inputs and expected criterion
We suppose that sequences of uncertainties 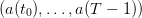 are random variables with a
known probability distribution ℙ on the set
are random variables with a
known probability distribution ℙ on the set 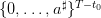 .
.
We suppose that the random variables 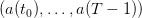 are independent with
distribution
are independent with
distribution 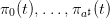 on the set
on the set 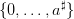 :
:
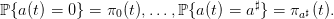 | (7) |
Notice that the random variables 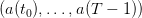 are independent, but that they are not
necessarily identically distributed. This allows us to account for seasonal effects (more rain in
autumn and winter).
are independent, but that they are not
necessarily identically distributed. This allows us to account for seasonal effects (more rain in
autumn and winter).
To each strategy Rule, we associate the expected payoff
![∑T−1
𝔼 [CritRule(t0,S0,a(⋅))] = 𝔼[ p(t)q(t) + UtilFin (T, S(T ))],
t=t0](dam_viability26x.png) | (8) |
where the expectation 𝔼 is taken with respect to the probability ℙ.
2 Maximizing the expected payoff and computing the resulting probability to satisfy the
constraint
2.1 Dynamic programming equation
The dynamic programming equation associated with the problem of maximizing the expected
payoff (8)
![T∑− 1
max 𝔼[ p(t)q(t) + UtilFin (T, S(T ))]
t=t0](dam_viability27x.png) | (9) |
is
![final payoff
◜-------◞◟------◝
V (T,S ) = UtilFin (T, S(T )),
♯
V(t,S ) = max ♯ 𝔼a(t)[ p◟(◝t)◜q◞ +V (t + 1,m◟in-{S-,S-−◝◜-q +-a-(t)}◞ )],
q∈{0,1,2,...,min{S,q }} instant. payoff future stock volume](dam_viability28x.png) | (10) |
where the expectation 𝔼 is taken with respect to the probability in (7).
2.2 Data for the numerical simulations
We know will make numerical simulations, and try different strategies. We shall consider a daily
management over one year
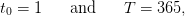 | (11) |
with
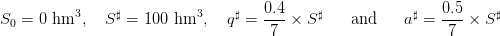 | (12) |
where we say that, during one week, one can turbine at maximum 40% of the dam volume, and
that during one week of full water inflows, an empty dam can be half-filled.
The sequence of prices is known in advance. We shall produce it by one sample from the
expression
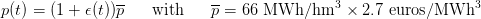 | (13) |
where 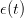 is drawn from a sequence of i.i.d. uniform random variables in
is drawn from a sequence of i.i.d. uniform random variables in ![[− 1∕2,1 ∕2]](dam_viability33x.png) .
.
The probability of water inflows (from zero to the maximum 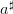 ) is known in
advance.
) is known in
advance.
Copy the following Scilab code into a file DamData.sce.
volume_max=100;
volume_min=0; control_max=0.4/7*volume_max; control_max=control_max+1;
tt0=1; horizon=365; TT=tt0:(horizon-1); bTT=tt0:(horizon);
price=66*2.7; price=price*(1/2+0.5*(rand(TT)-1/2));
uncertainty_max=floor(0.5/7*volume_max); uncertainty=[0:uncertainty_max];
unnormalized_proba=cumsum(ones(uncertainty))-1; proba1=unnormalized_proba/sum(unnormalized_proba);
proba182=proba1($:-1:1);
Simulations=50; WW=zeros(Simulations,horizon-tt0+1); for ss=1:Simulations do
for tt=bTT do proba=(1-sin(%pi*tt/365))*proba1+sin(%pi*tt/365)*proba182;
WW(ss,tt)=dsearch(rand(),cumsum(proba)); end end Scenarios=WW;
xset("window",1);xbasc(); plot2d2(bTT,Scenarios')
Copy the following Scilab macros into the same file DamData.sce.
In the macro trajectories, the output CC is the mean payoff averaged over the scenarios: by
the law of large numbers, CC is an approximation of the expected payoff if the number of scenarios
is large enough (Monte Carlo method).
function ssdot=dynamics(ss,qq,aa) ssdot=max(volume_min,min(volume_max,ss-qq+aa));
endfunction function c=instant_payoff(tt,ss,qq,aa)
c=price(tt)*qq; endfunction
function c=final_payoff(tt,ss) c=0; endfunction
function [SS,QQ,CC]=trajectories(SS0,scenarios,policy) SS=[]; QQ=[]; CC=[];
nb_simulations=size(scenarios,'r'); for simu=1:nb_simulations do ss=SS0; qq=[];
cc=0; aa=scenarios(simu,:); for tt=TT do qq=[qq,policy(tt,ss($))];
ss=[ss,dynamics(ss($),qq($),aa(tt))]; cc=cc+instant_payoff(tt,ss($),qq($),aa(tt));
end cc=cc+final_payoff(TT($),ss($)); SS=[SS;ss]; QQ=[QQ;qq];
CC=[CC;cc]; end disp('The payoff is '+string(mean(CC))); endfunction
2.3 Scilab code for the additive stochastic dynamic programming equation
Copy the following Scilab code into the file Damoptimality.sce.
states=[0:volume_max];
controls=[0:control_max]; cardinal_states=prod(size(states)); cardinal_controls=prod(size(controls));
cardinal_uncertainty=prod(size(uncertainty)); state_min=min(states);
state_max=max(states);
function [FEEDBACK,VALUE]=SDP(FINAL_PAYOFF) VALUE=zeros(bTT'*states);
FEEDBACK=zeros(TT'*states); VALUE(horizon,:)=FINAL_PAYOFF;
for tt=TT($:-1:1) do loc=zeros(cardinal_controls,cardinal_states);
for jj=1:cardinal_controls do hh=controls(jj); loc(jj,:)=0;
for dd=1:cardinal_uncertainty do
ww=uncertainty(dd); loc(jj,:)=loc(jj,:)+ ...
proba(dd)*(-1/%eps*bool2s(states < hh)+bool2s(states >= hh)) .* ...
(instant_payoff(tt,states,hh,ww)+ ...
VALUE(tt+1,dynamics(states,hh,ww)-state_min+1)); end; end
[mmn,jjn]=min(loc,'r'); [mmx,jjx]=max(loc,'r');
VALUE(tt,:)=mmx;
FEEDBACK(tt,:)=controls(jjx); end endfunction
We first consider that the final “value of water” is zero:
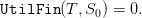 | (14) |
zero_final_payoff_vector=zeros(states);
[FEEDBACK,VALUE]=SDP(zero_final_payoff_vector);
function uu=optimal_rule(tt,xx) uu=FEEDBACK(tt,xx-state_min+1);
endfunction SS0=0;
[SS,HH,CC]=trajectories(SS0,Scenarios,optimal_rule); xset("window",10); plot2d(bTT,SS')
xtitle('Stock volumes in a dam following an optimal strategywith a zero final value of water', ...
'(time)','(volume)') xset("window",20);xbasc();
histplot(100,CC) xtitle('Histogram of the optimal payoff with a zero final value of water')
disp('The minimum of the optimal payoff is '+string(min(CC)));
disp('The mean of the optimal payoff is '+string(mean(CC)));
disp('The maximum of the optimal payoff is '+string(max(CC)));
Question 1 Picture the trajectories of the stocks corresponding to the optimal strategy.
Evaluate the optimal expected payoff, and compare it with the value function 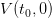 evaluated at the initial time t0 and the initial stock
evaluated at the initial time t0 and the initial stock 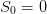 . Explain why these two quantities
should be close. What do you observe for the final stocks? Explain why.
. Explain why these two quantities
should be close. What do you observe for the final stocks? Explain why.
2.4 Optimal strategy when the final “value of water” is not zero
Till now, there was no gain in leaving water in the dam at the ultimate decision period. From now
on, we consider that the “value of water” 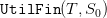 is given by
is given by
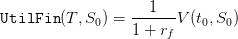 | (15) |
where 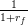 is a discount factor. We shall take
is a discount factor. We shall take 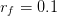 when
when 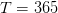 days.
days.
final_payoff_vector=(1/(1+0.1))*VALUE(1,:);
Copy the following Scilab code into the file DamOptimality.sce.
[FEEDBACK,VALUE]=SDP(final_payoff_vector); function uu=optimal_rule(tt,xx)
uu=FEEDBACK(tt,xx-state_min+1); endfunction
[SS,HH,CC]=trajectories(SS0,Scenarios,optimal_rule); xset("window",10); plot2d(bTT,SS')
xtitle('Stock volumes in a dam following an optimal strategy with a final value of water', ...
'(time)','(volume)') xset("window",20);xbasc();
histplot(100,CC) xtitle('Histogram of the optimal payoff with a final value of water')
disp('The minimum of the optimal payoff is '+string(min(CC)));
disp('The mean of the optimal payoff is '+string(mean(CC)));
disp('The maximum of the optimal payoff is '+string(max(CC)));
2.5 Evaluation of the probability to satisfy the tourism constraint
Let 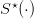 denote an optimal stock trajectory.
denote an optimal stock trajectory.
Question 3 Evaluate the probability
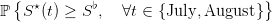 | (16) |
that the water volume 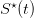 remains above F% of
remains above F% of 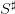 during the months of July and August,
where F% varies between 0% and 100%.
during the months of July and August,
where F% varies between 0% and 100%.
Summer=([1:horizon] >= horizon/2 & [1:horizon] <= horizon/2+2*30*horizon/364); VP=[]
for jj=0:100 do VP=[VP,mean(bool2s(min(SS(:,Summer),'c') >= jj/100*volume_max))];
end xset("window",30);xbasc(); plot(0:100,VP)
xtitle('Probability that the summer tourism constraint is satisfied under the optimal strategy with a final value of water', ...
'(guaranteed fraction of dam volume)','(probability)')
3 Maximizing the viability probability to guarantee jointly payoff and summer water
volume
The payoff at time t ∈ 𝕋 is
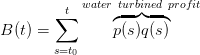
and
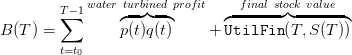
We propose an alternative stochastic viability formulation to (9)-(16) under the
form
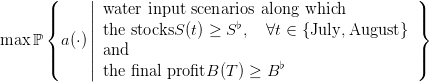 | (17) |
3.1 Multiplicative dynamic programming equation
The dynamic programming equation associated with the problem of maximizing the viability
probability (17) is
![final constraint
◜--◞◟-◝
V (T,S,B ) = 1{B≥B ♭} ,
V (T − 1,S,B ) = max 𝔼a (T− 1)[1 ♭
q∈ {0,1,2,...,min{S,q♯}} {S≥S ,T−1∈{July,August}
×V (t + 1,min {S♯,S − q + a(T − 1)},
B + p(T − 1)q + UtilFin (T,min {S♯,S − q + a(T − 1)})],
instantaneous constraint
◜--------◞◟---------◝
V(t,S,B ) = max ♯ 𝔼a (t)[1{S(t)≥S♭,t∈{July,August}}
q∈ {0,1,2,...,min{S,q}}♯
×V (t + 1,m◟in-{S-,S(t) −◝◜-q(t) +-a(t)}◞, B◟-+◝p◜(t)q◞ )], ∀t = t0,...,T − 2,
future stock volume future payoff](dam_viability57x.png) | (18) |
where the expectation 𝔼 is taken with respect to the probability (7). Notice that the equation for
t = T − 1 takes into account the term 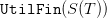 in the payoff.
in the payoff.
3.2 Scilab code for the multiplicative stochastic dynamic programming equation
Copy the following Scilab code into the file DamViability.sce.
horizon=10;
SSmax=volume_max; nb_SS=SSmax+1; state_PP=0:(horizon*SSmax); nb_PP=length(state_PP);
PPmax=max(state_PP); controls=0:nb_SS; nb_CC=length(controls);
volume_max=10; SSmax=volume_max;
nb_SS=SSmax+1; state_PP=0:(horizon*SSmax); nb_PP=length(state_PP); PPmax=max(state_PP);
controls=linspace(0,SSmax+1,10); nb_CC=length(controls);
uncertainties=0:1; nb_WW=length(uncertainties); proba=ones(1,nb_WW)/nb_WW;
function [FEEDBACK,VALUE]=MSDP(SS_min,PP_min)
VALUE=list(); FEEDBACK=list();
VALUE(horizon)=ones(nb_SS,1)*bool2s(state_PP >= PP_min); shift=[(horizon-1):(-1):1];
for tt=shift do VVdot=VALUE(tt+1); VV=zeros(VVdot); for ss=1:nb_SS do
SS=ss-1; if SS >= SS_min(tt) then for pp=1:nb_PP do PP=pp-1;
locext=[]; for cc=1:ss do
UU=cc-1; locint=0; for oo=1:nb_WW do
ww=uncertainties(oo); SSdot=(min(SSmax,SS-UU+ww));
ssdot=SSdot+1; Ppdot=(min(PPmax-1, ...
PP+price(tt)*UU+bool2s(tt==horizon-1)*final_payoff(tt,ssdot)));
ppdot=min(round(ppdot/PPmax)+1,nb_PP);
locint=locint+proba(oo)*VVdot(ssdot,ppdot);
end; locext=[locext,locint];
end; VV(ss,pp)=max(locext);
end; end;
end; VALUE(tt)=VV; end; endfunction
3.3 Maximal viability probability function and viability kernels
Question 4 Compute the maximal viability probability. Deduce the viability kernels with
confidence levels 100%, 95% and 90%.
stacksize('max'); PPmin=0.13*PPmax; SSmin=0.89*SSmax;
[FEEDBACK,VALUE]=MSDP(SSmin*Summer,PPmin)
3.4 Maximal viability probability as a function of guaranteed thresholds
Copy the following Scilab code into the file DamViability.sce.
precision=2; Thresholds_EE=linspace(0.1,0.15,precision)*PPmax;
nb_EE=length(Thresholds_EE); Thresholds_BB=linspace(0.75,0.99,precision)*SSmax;
nb_BB=length(Thresholds_BB); ViabProba=zeros(nb_BB,nb_EE);
for bb=1:nb_BB do SS_min=Thresholds_BB(bb)*Summer; for ee=1:nb_EE do
PP_min=Thresholds_EE(ee); [FEEDBACK,VALUE]=MSDP(SS_min,PP_min);
VV=VALUE(1); ViabProba(bb,ee)=VV(nb_SS-2,1); end
end save("ViabStoch.dat",ViabProba)
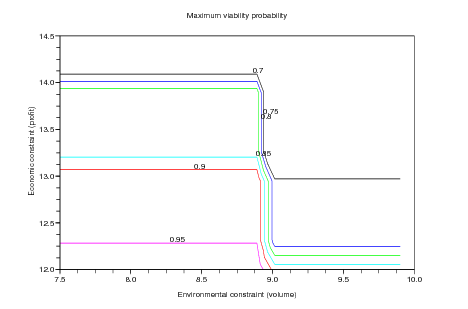
Question 5 Launch the above code (maybe you will have to reduce the time step, or the
horizon, and adapt the code in consequence if the computation takes too much time). Visualize
the maximal viability probability starting from an almost full dam. Draw iso-probability
curves. Comment on what you observe.
SP=10^6; SP=10; SC=10; SC=2; xset('window',1);
xset('colormap',jetcolormap(20));
plot3d1(SC*Thresholds_BB,Thresholds_EE,SP*ViabProba);
xtitle("Maximum viability probability","Environmental constr. (volume)", ...
"Economic constraint (profit)")
xset('window',10);contour(Thresholds_BB,Thresholds_EE,ViabProba,[0.7:0.05:1]);
xtitle("Maximum viability probability","Environmental constraint (volume)", ...
"Economic constraint (profit)")
References
D. P. Bertsekas. Dynamic Programming and Optimal Control. Athena Scientific,
Belmont, Massachusets, second edition, 2000. Volumes 1 and 2.
M. De Lara and L. Doyen. Sustainable Management of Natural Resources. Mathematical
Models and Methods. Springer-Verlag, Berlin, 2008.
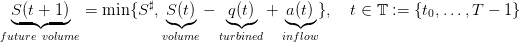
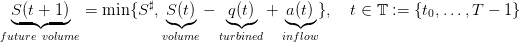
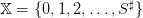 , made of water volumes, where
, made of water volumes, where 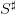 is the maximum
dam volume,
is the maximum
dam volume,
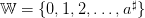
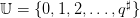 , where q♯ is the maximum which can be turbined by time unit
(and produce electricity),
, where q♯ is the maximum which can be turbined by time unit
(and produce electricity),
![s(t) = [S (t) − q(t) + a(t) − S ♯]
+](dam_viability5x.png) the spilled volume
the spilled volume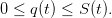
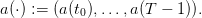

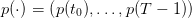
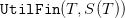 gives value to the water volume in the dam at the horizon
T.
gives value to the water volume in the dam at the horizon
T.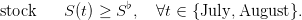
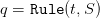 to any state S of dam stock
volume and to any decision period t ∈ 𝕋. Once given, we obtain uncertain volume trajectories
to any state S of dam stock
volume and to any decision period t ∈ 𝕋. Once given, we obtain uncertain volume trajectories
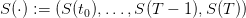 and turbined trajectories
and turbined trajectories 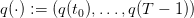 produced by the “closed-loop” dynamics
produced by the “closed-loop” dynamics
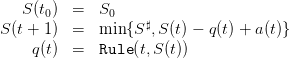
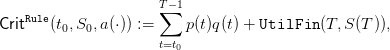
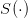 and
and 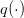 are given by (5).
are given by (5).
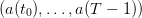 are random variables with a
known probability distribution ℙ on the set
are random variables with a
known probability distribution ℙ on the set 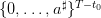 .
.
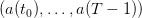 are independent with
distribution
are independent with
distribution 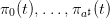 on the set
on the set 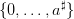 :
:
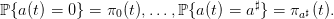
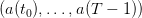 are independent, but that they are not
necessarily identically distributed. This allows us to account for seasonal effects (more rain in
autumn and winter).
are independent, but that they are not
necessarily identically distributed. This allows us to account for seasonal effects (more rain in
autumn and winter).
![∑T−1
𝔼 [CritRule(t0,S0,a(⋅))] = 𝔼[ p(t)q(t) + UtilFin (T, S(T ))],
t=t0](dam_viability26x.png)
![T∑− 1
max 𝔼[ p(t)q(t) + UtilFin (T, S(T ))]
t=t0](dam_viability27x.png)
![final payoff
◜-------◞◟------◝
V (T,S ) = UtilFin (T, S(T )),
♯
V(t,S ) = max ♯ 𝔼a(t)[ p◟(◝t)◜q◞ +V (t + 1,m◟in-{S-,S-−◝◜-q +-a-(t)}◞ )],
q∈{0,1,2,...,min{S,q }} instant. payoff future stock volume](dam_viability28x.png)
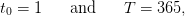
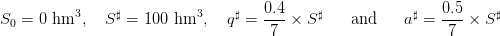
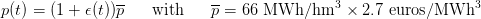
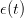 is drawn from a sequence of i.i.d. uniform random variables in
is drawn from a sequence of i.i.d. uniform random variables in ![[− 1∕2,1 ∕2]](dam_viability33x.png) .
.
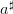 ) is known in
advance.1
) is known in
advance.1
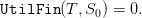
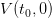 evaluated at the initial time t0 and the initial stock
evaluated at the initial time t0 and the initial stock 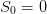 . Explain why these two quantities
should be close. What do you observe for the final stocks? Explain why.
. Explain why these two quantities
should be close. What do you observe for the final stocks? Explain why.
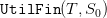 is given by
is given by
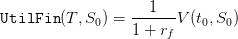
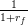 is a discount factor. We shall take
is a discount factor. We shall take 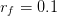 when
when 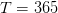 days.
days.
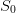 , and
compare them with the value function
, and
compare them with the value function 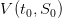 evaluated at the initial time t0 and the
initial stock
evaluated at the initial time t0 and the
initial stock 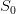 . Display the histogram of the optimal payoff. Compare the mean of the
optimal payoff with the upper and lower bounds of the distribution.
. Display the histogram of the optimal payoff. Compare the mean of the
optimal payoff with the upper and lower bounds of the distribution.
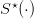 denote an optimal stock trajectory.
denote an optimal stock trajectory. 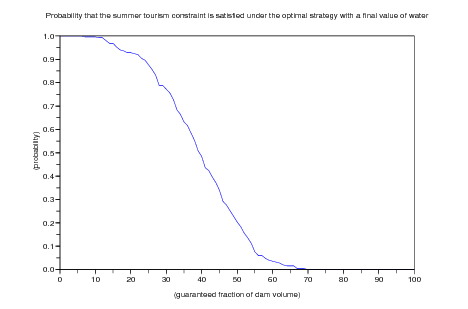
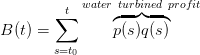
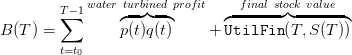
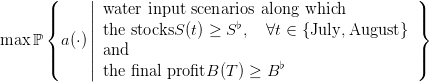
![final constraint
◜--◞◟-◝
V (T,S,B ) = 1{B≥B ♭} ,
V (T − 1,S,B ) = max 𝔼a (T− 1)[1 ♭
q∈ {0,1,2,...,min{S,q♯}} {S≥S ,T−1∈{July,August}
×V (t + 1,min {S♯,S − q + a(T − 1)},
B + p(T − 1)q + UtilFin (T,min {S♯,S − q + a(T − 1)})],
instantaneous constraint
◜--------◞◟---------◝
V(t,S,B ) = max ♯ 𝔼a (t)[1{S(t)≥S♭,t∈{July,August}}
q∈ {0,1,2,...,min{S,q}}♯
×V (t + 1,m◟in-{S-,S(t) −◝◜-q(t) +-a(t)}◞, B◟-+◝p◜(t)q◞ )], ∀t = t0,...,T − 2,
future stock volume future payoff](dam_viability57x.png)
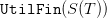 in the payoff.
in the payoff.