Abstract
1
1.1
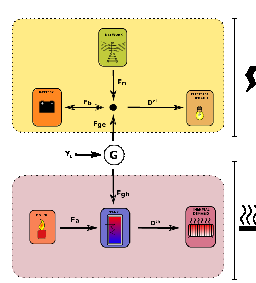
We consider here a house equipped with a thermal hot water tank, a combined heat and power generator (CHP) and a battery. This house has two systems to satisfy its energetical needs: a thermal system for heating, and an electrical system to satisfy its electrical demand. These two systems are coupled together via the CHP, rendering the optimal control difficult to find.
The CHP is a generator which produces both electricity and heat while burning gas. The power of the CHP can not be modulated: it produces always the same amount of heat and electricity.
A battery can store the potential surplus of electricity (especially when demand is low), and the house is connected to the grid to import electricy if necessary. The heat produced by the CHP is stored in a hot water tank. Hot water is withdrawn from this tank to satisfy thermal demand.
We aim to decrease the operational costs while taking into account that:
1.2
We model our system with discrete linear equations, stating the evolution of the system between two timesteps t and t + 1. Controls are computed at the begining of the time interval [t,t + 1[, and are applied all along this interval. That gives a discrete time optimal control problem.
We control here the system during one day, at a 15mn timestep.
1.2.1
Bt is the energy stored inside the battery at time t. The battery’s dynamic is the following:
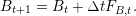 | (1) |
Battery’s constraints The battery’s level must remain greater than a given level otherwise its life expectancy decreases much more quickly. Usually, it is specified that this level remains between 30% and 90% of the maximum level of charge. The charge and discharge are also bounded by a maximum rampage rate ΔB. These two constraints write:
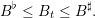 | (2) |
and
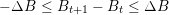 | (3) |
1.2.2
We have two inputs for the hot water tank:
and one output: the thermal demand of the house Dtth.
We denote the tank’s level Ht, denoting the energy stored inside the tank at time t (in kWh). This level is bounded:
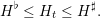 | (4) |
The hot water tank is modelled with:
All these equations are designed so as the constraints 4 are satisfied for all demand Dtth.
The recourse variable Fth,t+1 is penalized afterward in the cost function.
1.3
Electrical exchange We denote FN,t the electricity imported from the grid at time t.
The balance equation between production and demand in the upper electric part in Figure 1.1 writes:
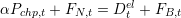 | (6) |
The electricity imported from the network is being paid at a tariff πtel, which
depends upon time. The price scenario  πtiel,…,πTfel
πtiel,…,πTfel is supposed to be known in
advance.
is supposed to be known in
advance.
Operational costs Costs between [t,t + 1[ are:
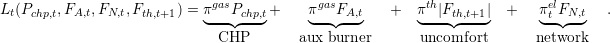 | (7) |
In (7), costs of different devices are considered:
1.4
We can now write the optimization criterion:
![T∑−1
min 𝔼[ Lt(Pchp,t,FA,t,FN,t,Fth,t+1)]
u t=0](domestic_microgrid13x.png) | (8) |
![s.t.
Bt+1 = Bt + ΔtFB,t
B ♭ ≤ Bt ≤ B♯
♭ ♯
ΔB ≤ Bt+1 −thBt ≤ ΔB
Ht+1 = Ht + Δt [(1 − α)Pchp,t + FA,t − Dt♭ + Fth,t+1♯]
H ≤ Ht ≤ H](domestic_microgrid14x.png) |
We recall the different notations we used previously in Table 1.
| State variables
| ||
| Bt | Battery level | kWh |
| Ht | Tank level | kWh |
| Control variables
| ||
| Pchp,t | CHP power | kW |
| FB,t | Energy exchanged with the battery | kW |
| FA,t | Production of auxiliary burner | kW |
| Noises
| ||
| Dtel | Electrical demand | kW |
| Dtth | Thermal demand | kW |
| Parameters
| ||
| πel | Electricity price | euros |
| πgas | Gas price | euros |
| πth | Price of uncomfort | euros |
2
The states, controls and perturbations are now denoted:
We suppose that states belong to a static set xt ∈ 𝕏, so do control ut ∈ 𝕌.
A demand scenarios is a sequence of demands from time t0 up to Tf − 1.
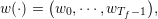 | (10) |
where for all t, wt = (Dtel,Dtth).
w(⋅) is supposed to be the realization of a stochastic process (Wt)t=0Tf.
2.1
An admissible policy γ : 𝕋 × 𝕏 → 𝕌 assigns a control u = γ(t,x) ∈ 𝕌 to any time t ∈ 𝕋 and to any state x ∈ 𝕏,
Given an admissible policy γ and given a demand scenario w(.) we are able to build trajectories x(⋅) for battery and hot water tank: the dynamic is initiate at time t0 by:
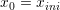 |
and the trajectory is computed step by step with following equation:
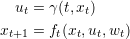
We obtain the payoff associated to the demand scenario w(⋅):
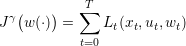 | (11) |
The expected payoff associated with the policy γ is:
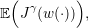 | (12) |
where the expectation 𝔼 is taken with respect to the product probability ℙ. We evaluate
(12) by the Monte-Carlo method using Ns scenarios  w1(⋅),
w1(⋅), ,wNs(.)
,wNs(.) :
:
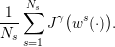 | (13) |
In the next, we will evaluate each algorithm with this method:
The following code generate scenarios that can be used for simulation:
The data used for scenarios generation can be obtained here in zip format code.zip or tgz code.tgz.
2.2
The function simulate is used to simulate a policy:
Question 2
We consider a first policy, given by the echelon-based heuristic:
Question 3
3
We are going to compare two policies to solve the problem (8):
We will assess each policy along the scenarios generated in Question 1. However, these policies need to consider some scenarios as input for their algorithms. To be fair, we will use optimization scenarios distinct from the assessment scenarios considered in Question 1.
As we are considering a real world problem, we do not have that much scenarios recorded. That is why we use only 30 scenarios for optimization and 30 scenarios for assessment.
3.1
As time goes on, MPC computes at the beginning of each period 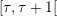 the
control as a function of the current time and state xτ. Here are the details:
the
control as a function of the current time and state xτ. Here are the details:
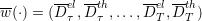 of demands
(forecast) with the optimization scenarios.
of demands
(forecast) with the optimization scenarios.
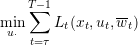 | (14) |
 |
The problem (14) returns a control ut♯ for all time t and state xt. This problem gives the MPC policy:
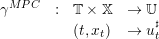 | (15) |
γMPC is implemented in the function policy_mpc:
Question 4
3.2
Dynamic programming works in two stages: an offline stage where value functions are computed, and an online stage where these functions are used to compute a policy.
Offline: computation of value functions

![[ ( )]
Vt(xt) = min 𝔼 Lt(xt,ut,wt)+ Vt+1 ft(xt,ut,wt )
ut∈𝕌](domestic_microgrid31x.png)
Online: construction of the policy
DP policy computes at the beginning of each period 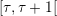 the control as a
function of the current time τ and state xτ:
the control as a
function of the current time τ and state xτ:
![♯ [ ( )]
uτ ∈ arugm∈i𝕌n 𝔼 Lt(xτ,uτ,w τ)+ Vτ+1 ft(xτ,uτ,wτ)
τ](domestic_microgrid33x.png)
xt+1 = ft(xt,ut,wt) is a functionnal relation, lying in the continuous state space 𝕏. As we use a computer we will discretize state and control spaces to implement dynamic programming. We restrict ourself to a subset 𝕏d ⊂ 𝕏 for states and 𝕌d ⊂ 𝕌 for controls.
Implementation The Dynamic Programming solver is already implemented. It is called by the function:
which return the Bellman functions in a multidimensional array Vs.
Question 5 Generate marginal laws with the help of the given optimization scenarios and the function generate_laws.
Question 6
Question 7 Plot different Bellman functions with the help of the function plot_bellman_functions. Comment the evolution of the shape of these functions along time.
Question 8
3.3
We want to compare three different features for each algorithm:
| Policy | Offline computation time | Online computation time | Average Costs |
| Heuristic | |||
| MPC | |||
| DP | |||
Question 9 Fill the Table 2 with the results previously obtained.
A
We have two stocks: a battery and thermal tank. Even if the dynamic programming principle still holds, the numerical implementation is not as straightforward as in the unidimensional case.
A.1
We need to discretize state and control spaces to apply dynamic programming. We restrict ourself to a subset 𝕏d ⊂ 𝕏 for states and 𝕌d ⊂ 𝕌 for controls. The policy find by dynamic programming is then suboptimal.
To iterate upon different states in 𝕏d, we define a bijective mapping between 𝕏d and ℕ. This mapping is written:
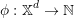 | (16) |
Question 10
A.2
With this discretization, we know the value of Bellman function V only upon the grid 𝕏d, and not upon the whole state 𝕏.
We recall that the next state is given by the state equation: However, even if xt ∈ 𝕏d and ut ∈ 𝕌d, we can not ensure that xt+1 ∈ 𝕏d to compute future cost V t+1(xt+1). That is why we need to use an interpolation scheme to interpolate V t+1(xt+1) with the values of V t+1 in 𝕏d.
Question 11 With the notation introduced in Figure 4, write the linear interpolation of xt+1 w.r.t Xid.