![∑𝜃
S𝜃 := [f(xt,et) − ut].
t=0](english_Plant_alloc_I0x.png)
“ Herbs often flower in their first year and then die, roots and all, after setting seed. Plants that flower once and then die are monocarpic.
Many monocarps are annual but a few species have long lives. Bamboos are grasses but they grow to unusually large size. One Japanese species, Phyllostachys bambusoides, waits 120 years to flower (Janzen, 1976).
Most trees flower repeatedly. However, Foster (1977) has characterized Tachigalia versicolor as a ’suicidal neotropical tree’. After reaching heights of 30-40 m, it flowers once and then dies. ”
(Cited from Mark Kot, Elements of Mathematical Ecology, Cambridge University Press, 2001)
Mammals and other organisms present determinate growth: they stop growth when they become mature and start to reproduce. But many animals and plants, such as fishes, snakes, clams, etc. experience indeterminate growth: they life-history shows trade-offs between growth and reproductiwe havelong their lifetime.
The model of single plant growth of [1] depends on three factors:
The dynamics is a follows.
In the first part of the paper, Amir and Cohen consider one source of stochasticity, namely 𝜃, before introducing also the environment e as random. The dynamics above is randomly aborted at 𝜃 giving the annual reproductive yield per plant:
![∑𝜃
S𝜃 := [f(xt,et) − ut].
t=0](english_Plant_alloc_I0x.png) | (1) |
Note that the constraint 0 ≤ ut ≤ f(xt,et) implies two biological as:
Consider an annual plant which grows and reproduces according to the following dynamics
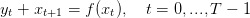 | (2) |
where
Here are the general assumptions on the growth function :
Let us assume that the plant lives for a random number 𝜃 of periods, with the random variable 𝜃 following a geometric law with parameter β, survival probability :
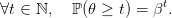 | (3) |
We assume that death occurs at the end of a period. Thus, on the event {𝜃 = t}, the plant dies at the end of period [t,t + 1[, leaving reproductive biomass f(xt) = f(x𝜃) and vegetative biomass xt+1 = x𝜃+1 = 0.
Consider a plant with vegetative biomass xt at the beginning of period [t,t + 1[. It will generate total biomass f(xt) at the end of the period. This biomass will be split between reproductive biomass yt and future vegetative biomass xt+1. What we call here a “decision” for the plant corresponds to the choice of an allocation between reproductive biomass and future vegetative biomass.
Let us introduce the decision variable
![ut = xt+1 ∈ [0,f(xt)].](english_Plant_alloc_I3x.png) | (4) |
We define a strategy for the plant as a sequence of decisions
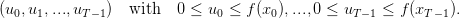 | (5) |
Mathematically speaking, a strategy is a mapping
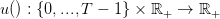 | (6) |
such that u(t,x) ∈ [0,f(x)].
We shall say that a strategy is optimal if it maximizes the mathematical expectation of the fitness (individual contribution to future generations):
![(T−∑ 1)∧𝜃
J (u(.)) = 𝔼 ( [f(xt) − ut]), u(.) = (u0,u1,...,uT− 1).
t=0](english_Plant_alloc_I6x.png) | (7) |
Here, the fitness is defined as the cumulated reproductive biomass at the end of the growing season (the annual reproductive yield for an annual plant).
An optimal trajectory is any sequence (x0,...,xT ) generated by
 | (8) |
where u♯ is an optimal strategy.
Consider various plants with various strategies. At the end of the growing season, those plants with an optimal strategy should, in the mean (because a mathematical expectation is maximized), be relatively more numerous than the others. Season after season, their relative number would grow.
When variability is between individuals within the same season (independent lifetimes) and when the populations are sufficiently large, the law of large numbers applies and this justifies the expected value of the annual reproductive yield as appropriate measure of fitness. Other approaches define an optimal strategy as one not susceptible to be invadable by a mutant.
Here, the expectatiwe above is with respect to the only source of randomness, namely 𝜃.
Thus, identifying optimal strategies amounts to solving
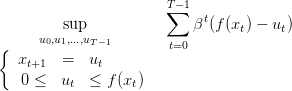 | (10) |
This is a deterministic dynamic optimization problem with additive criterion characterized by
The dynamic programming equation (dpe) is
 | (11) |
Denoting
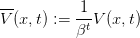 | (12) |
the dpe may equivalently be written as
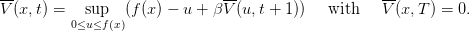 | (13) |
Optimal strategies u♯ are solution of
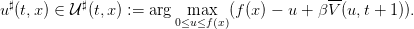 | (14) |
Question 2 Show that (x,T − 1) = f(x) and that the last optimal decision u♯(T − 1,x) consists in allocating all available biomass at the end of period [T − 1,T[ into reproductive biomass, and thus die at T.
There is no gain in terms of offspring to keep vegetative biomass at the end of the last period.
Let us suppose here that
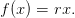 | (15) |
Question 3
Let us suppose here that
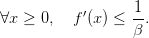 | (16) |
Question 4 Show that, for t = 0,...,T − 1, (t,x) = f(x) and 𝒰t♯(t,x) = {0}. Describe the profile of an optimal trajectory.
Marginalist economic interpretation: whatever the plant size, the expected marginal gain in future biomass (βf′(x)) is always less than the direct gain in offspring (+1 by renouncing to growing by one unit).
Let us suppose here that
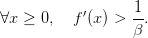 | (17) |
Question 5 Show that, for t = 0,...,T − 1, 𝒰t♯(t,x) = {f(x)}. Describe the profile of an optimal trajectory.
Marginalist economic interpretation: whatever the plant size, the expected marginal gain in future biomass (βf′(x)) is always greater than the direct gain in offspring (+1). An example is given by the ’suicidal neotropical tree’ Tachigalia versicolor.
Let us suppose here that
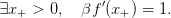 | (18) |
Together with the target x+, let us define the threshold
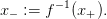 | (19) |
Thus, the function u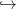 − u + βV (u,t) is nondecreasing up to x+, then nonincreasing.
− u + βV (u,t) is nondecreasing up to x+, then nonincreasing.
Question 6 Show that an optimal decision rule at period T − 2 is
Question 7 Show that
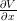 (x+,T − 2) = 1;
(x+,T − 2) = 1;
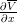 (x,T − 2) is decreasing.
(x,T − 2) is decreasing.Deduce from this that optimal decision rules at periods T − 2 and T − 3 coincide.
Going backward, one may show that, for all t = 0,...,T − 2, growing without reproducing when vegetative biomass is under threshold x− and growing up to the target x+ if not is the optimal strategy (except at the last season).
Marginalist economic interpretation: at the target x+, the expected marginal gain in future biomass (βf′(x+)) is equal to the direct gain in offspring (+1). Examples are given by mammals (including whales and humans).
Let us take
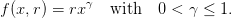 | (20) |
To facilitate computer programming, the control is no longer ut ∈ [0,f(xt)], but
![ut
vt :=------∈ [0,1] (vt = 0 if f(xt) = 0).
f (xt)](english_Plant_alloc_I23x.png) | (21) |
Thus, this control v belongs to a fixed interval [0, 1], contrarily to u ∈ [0,f(x)].
We incorporate the random time 𝜃 directly in a stochastic dynamics as follows
![xt+1 = F (xt,vt,st), t = 0,...,T − 1, vt ∈ [0,1], st ∈ {0, 1}.](english_Plant_alloc_I24x.png) | (22) |
Here, st = 0 means that the plant dies at the end of period [t,t + 1[, while st = 1 corresponds to survival. The sequence s0,...,sT−1 is i.i.d. with binomial distribution ℙ(st = 1) = β.
Open a file plantI1.sci and write a Scilab function dyn_plant representing the growth function, depending on the state x (the value of the parameter r will be given later).
In the file plantI1.sci, write the fonction dyn_plant_control.
In the file plantI1.sci, write the following instantaneous and final costs functions.
In the file plantI1.sci, write the following Scilab macros:
In the file plantI1.sci, write the following Scilab function traj_feedback with arguments
and with outputs the corresponding state and control trajectories after feedback.
In the file plantI1.sci, write the following Scilab function total_cost with arguments
and with output the value of the additive criterion along state and control trajectories.
Open a file plantI1.sce. In this file, we will ask to load the macros in the file plantI1.sci and we will change the values of the following parameters.
Question 8 Compute state and control trajectories in closed loop with the different strategies strategy_X. Use for this Scilab function traj_feedback.
Compute corresponding fitness. Use for this Scilab function total_cost.
Draw state, control and fitness trajectories thanks to Scilab macro plot2d2.
Write these instructions in file plantI1.sce, and execute them by exec(’plantI1.sce’).
Question 9 Compare total fitness for the different strategies.
Question 11 In file plantI1.sci, write a Scilab function strategy_O ( _O for optimal), with arguments a state x and a time t, and with output following feedback rule:
Check, with the above theoretical results, that this strategy is optimal.
Question 12 Do the same questions as above with the following strategy.
Question 13 What do you observe when γ varies in [0, 1]?
We take
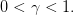 | (23) |
Copy the following parameters in a file plantI2.sce.
Copy the following code in file plantI2.sce. It provides the state and control discretizations, as well as instantaneous cost and final cost. See Programmation dynamique, macros generales.
Note that Scilab functions defined in Section 4 are now redefined.
Get the Scilab functions predec_succes, egal and discretisation from Programmation dynamique, macros generales and copy them in the file plantI2.sci, as well as the following function.
Copy the following code in file plantI2.sce.
Question 14 Check that the list of matrices matrix_transition indeed consists of transition matrices, that is with nonnegative coefficients summing to 1 on each row.
Get the Scilab functions Bell_stoch and trajopt from Programmation dynamique, macros generales and copy them in file plantI2.sci
Copy the following code in file plantI2.sce.
Question 15 Study the trajectories, and compare them with those obtained above.