Contents
Introduction
This pratical work will follow the example worked out in M. De Lara’s first lecture. The
computations will be performed using nsp (a Matlab like simulation language). In order to launch
nsp just use the Nsp entry in the menu Applications/Science. You will need a specific nsp toolbox
called qhull to perform Voronoi tesselation. In order to load it, just type within nsp:
exec('COURSES/qhullnsp/loader.sce');
1 The Problem
Consider two independent random variables 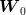 and
and 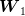 , each with a uniform probability
distribution over
, each with a uniform probability
distribution over ![[− 1,1]](voronoi2x.png) (zero mean, variance
(zero mean, variance 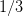 ). The unique decision variable
). The unique decision variable 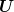 may
only use the observation of
may
only use the observation of 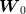 (which we view as the initial state
(which we view as the initial state 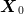 ). The final state
). The final state 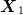 is equal to
is equal to 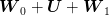 . The goal is to minimize
. The goal is to minimize 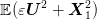 , where
, where  is a given
“small” positive number (“cheap control”). The statement is thus
is a given
“small” positive number (“cheap control”). The statement is thus
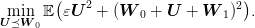 | (1) |
2 Exact Solution
We have that
The
last two terms in the right-hand side yield zero in expectation since 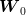 and
and  are centered
independent random variables and since
are centered
independent random variables and since 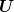 is measurable with respect to
is measurable with respect to 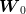 . The first two
terms yield twice the variance
. The first two
terms yield twice the variance 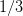 of the noises. Therefore, we remain with the problem of
minimizing
of the noises. Therefore, we remain with the problem of
minimizing
 | (2) |
by choosing  as a measurable function of
as a measurable function of 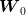 . One can see that the solution is given
by
. One can see that the solution is given
by
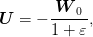
and the corresponding optimal cost is readily calculated to be
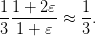 | (3) |
Question 1 Use the following code to recover previous results by both numerical integration
(nsp function intg) and Monte Carlo simulations. Choose and code an other feedback and
compare the associated cost with the optimal cost.
epsilon=1.E-2;
function u=feed(w0) u=-w0/(1+epsilon);endfunction;
function y=fcost(w0,feedback) u=feedback(w0); y=2/3+(1+epsilon)*u .^2+2*u .*w0; endfunction;
[cost,ea_estim]=intg(-1,1,fcost,args = feed,vecteval = %t); cost=cost/2;
W=grand(1,2500,'unf',-1,1); Y=fcost(W,feed); costmc=mean(Y);
3 Naive Monte Carlo Discretization

We now proceed to some discretization of this problem. To that purpose, we first consider 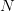 noise trajectories
noise trajectories 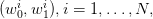 which are
which are 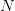 sample of the two-dimensional vector
sample of the two-dimensional vector
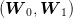 . Those samples will serve to approximate the cost expectation by a usual Monte
Carlo averaging.
. Those samples will serve to approximate the cost expectation by a usual Monte
Carlo averaging.
However, in this process, we must also consider 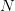 corresponding realizations
corresponding realizations 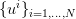 of the random decision variable
of the random decision variable 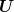 . But we must keep in mind that this random
variable should be measurable with respect to the first component
. But we must keep in mind that this random
variable should be measurable with respect to the first component 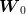 of the previous
vector.
of the previous
vector.
To that purpose, we impose the constraint
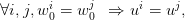 | (4) |
which prevents 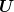 from taking different values whenever
from taking different values whenever 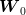 assumes the same value in any
two sample trajectories.
assumes the same value in any
two sample trajectories.
When Constraint (4) is never active, then we have to compute a different control value for each
sample and the cost is:
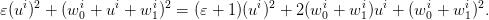 | (5) |
This expression must be minimized in 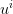 for every
for every 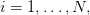 under the constraint (4). This
yields the optimal value
under the constraint (4). This
yields the optimal value
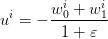 | (6) |
and the corresponding contribution to the cost 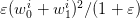 . This is of order
. This is of order  , and so
is the average over
, and so
is the average over 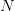 samples
samples
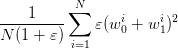 | (7) |
even when 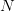 goes to infinity. This is far from the actual optimal cost given by (3).
goes to infinity. This is far from the actual optimal cost given by (3).
Question 2 Use the function grand to obtain a set of N=2500 samples of (W0,W1).
Assuming that the N values that you obtain for W0 are one by one distinct, compute the
optimal cost of the discrete problem.
Optional question: set N=1000000 and check if all the values for W0 are one by one distinct
(use function unique and type help unique to get the online manual). If not, propose a
modification of the code to handle this case in order to compute the discrete optimal cost.
4 What Is the Real Value of this “Solution”?
However, any admissible solution (any 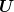 such that
such that 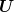 is measurable w.r.t.
is measurable w.r.t.  ) cannot
achieve a cost which is better than the optimal cost (3). The value (7) is just a “fake”
cost estimation. The resolution of the discretized problem derived from the previous
Monte Carlo procedure yielded an optimal value
) cannot
achieve a cost which is better than the optimal cost (3). The value (7) is just a “fake”
cost estimation. The resolution of the discretized problem derived from the previous
Monte Carlo procedure yielded an optimal value 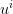 (see (6)) associated with each
sample noise trajectory represented by a point
(see (6)) associated with each
sample noise trajectory represented by a point 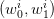 in the square
in the square ![[− 1,1 ]2](voronoi49x.png) . Hence,
before trying to evaluate the cost associated with this “solution”, we must first derive
from it an admissible solution for the original problem, that is, a random variable
. Hence,
before trying to evaluate the cost associated with this “solution”, we must first derive
from it an admissible solution for the original problem, that is, a random variable 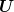 over
over ![Ω = [− 1,1]2](voronoi51x.png) , but with constant value along every vertical line of this square
(since the abscissa represents the first component
, but with constant value along every vertical line of this square
(since the abscissa represents the first component 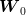 of the 2-dimensional noise
of the 2-dimensional noise
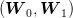 ).
).
A natural choice is as follows:
Since this is an admissible solution for the original (continuous) problem, the corresponding
cost value 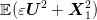 can be evaluated. Here, the expectation is over the argument
can be evaluated. Here, the expectation is over the argument 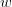 considered as a random variable over the square with uniform distribution (the calculation of this
expectation is done analytically).
considered as a random variable over the square with uniform distribution (the calculation of this
expectation is done analytically).
According to (2), this expected cost is easily evaluated as
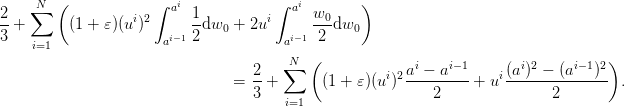 |
(9)
|
epsilon=1.E-2; N=2500; W=grand(2,N,'unf',-1,1); U=-(W(1,:)+W(2,:))/(1+epsilon);
cost=ZZZ,
5 Scenario Tree-based Discretization
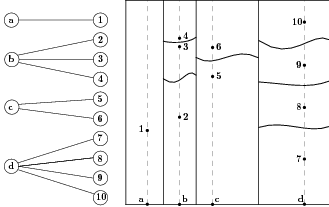 The question is thus: how to
formulate another constraint translating the informational constraint in the discretized problem
more effective than (4)? An obvious answer is that, in our collection of sample trajectories used in
the discrete optimization problem, there should really be distinct samples with the same value of
component
The question is thus: how to
formulate another constraint translating the informational constraint in the discretized problem
more effective than (4)? An obvious answer is that, in our collection of sample trajectories used in
the discrete optimization problem, there should really be distinct samples with the same value of
component 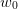 .
.
Admittedly, if the scenarios are produced randomly (according to the joint uniform probability
law of 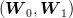 over the square
over the square ![[− 1,1] × [− 1,1]](voronoi86x.png) ), or if they have been recorded from real life
observations, there is a probability zero that a tree shape will pop up spontaneously, for any
arbitrary large but finite
), or if they have been recorded from real life
observations, there is a probability zero that a tree shape will pop up spontaneously, for any
arbitrary large but finite 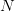 .
.
In the case of our example, since 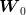 and
and 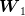 are known to be independent (the white
noise case), any element in a set of
are known to be independent (the white
noise case), any element in a set of 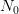 samples of
samples of 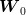 can be combined with the
same, or
can be combined with the
same, or 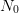 distinct, sets of
distinct, sets of 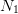 samples of
samples of 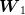 to produce such a tree. Even
if
to produce such a tree. Even
if 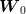 and
and 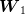 were not independent, one could first generate
were not independent, one could first generate 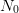 samples of
samples of
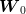 using the marginal probability law of this variable, and then, using each sample
using the marginal probability law of this variable, and then, using each sample
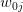 and the conditional probability law of
and the conditional probability law of 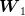 knowing that
knowing that 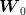 assumes the
value
assumes the
value 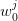 , one could generate
, one could generate 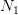 associated samples
associated samples 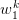 of
of 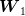 (“sons” of that
(“sons” of that
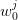 ).
).
To fix notations, we consider scenarios 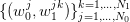 and we introduce the following
additional symbols:
and we introduce the following
additional symbols:
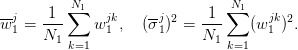 | (10) |
Notice that 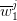 can be interpreted as an estimate of the conditional expectation of
can be interpreted as an estimate of the conditional expectation of 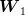 knowing that
knowing that 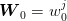 . Likewise,
. Likewise, 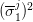 can be interpreted as an estimate of the conditional
second order moment.
can be interpreted as an estimate of the conditional
second order moment.
The cost of the discretized problem is
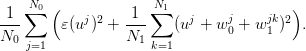
The minimizer is
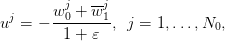 | (11) |
to be compared with (6). This yields the optimal cost
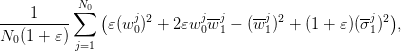 | (12) |
to be compared with (7) and (3). If we assume that the estimates (10) converge towards
their right values (respectively, 0 and 1/3) as 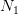 goes to infinity, then (12) gets close
to
goes to infinity, then (12) gets close
to
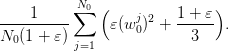
Now, the expression 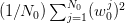 can also be viewed as an estimate of the second order
moment of
can also be viewed as an estimate of the second order
moment of 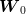 and, if we assume that it converges to the true value 1/3 when
and, if we assume that it converges to the true value 1/3 when 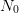 goes to
infinity, then we recover, in the limit, the true optimal cost (3). Therefore, unlike with the previous
naive Monte Carlo method (see (7)), here the optimal cost obtained in the discrete problem
appears to converge to the right value.
goes to
infinity, then we recover, in the limit, the true optimal cost (3). Therefore, unlike with the previous
naive Monte Carlo method (see (7)), here the optimal cost obtained in the discrete problem
appears to converge to the right value.
As we did earlier (see (9)), it is also interesting to evaluate the real cost associated with an
admissible solution derived from the collection of “optimal” values (11) by plugging those values
into the formula (8) (with 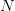 replaced by
replaced by 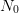 ). Again, we have appealed to a computer
program using 100 experiments, each consisting in:
). Again, we have appealed to a computer
program using 100 experiments, each consisting in:
- drawing
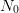 values
values 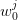 at random;
at random;
- associated with each of those values, drawing a set of
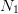 values
values  at random;
at random;
- computing the
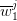 ’s (see (10)), the
’s (see (10)), the 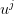 ’s (see (11)) and forming the admissible
solution (8) (
’s (see (11)) and forming the admissible
solution (8) (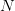 replaced by
replaced by 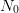 ) with those values after reordering the indices
) with those values after reordering the indices 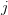 so that
so that 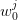 is increasing with
is increasing with 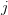 ;
;
- evaluating the true cost
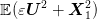 by analytic integration w.r.t. the couple
by analytic integration w.r.t. the couple
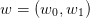 with uniform probability distribution over the square
with uniform probability distribution over the square ![2
[− 1,1]](voronoi136x.png) .
.
Question 4 Compute the optimal cost for the real problem obtained with the feedback (8) for
a given tree sample of (W0,W1). The optimal cost being itself a random variable, compute
by Monte Carlo its mean and standard deviation for different values of N.
epsilon=1.E-2; N0=50; W0=grand(1,N0,'unf',-1,1); N1=50;
W1=grand(N1,N0,'unf',-1,1);
W1m=mean(W1,1);
sig=mean(W1 .*W1,1);
6 Independent Discretizations of Noise and Information
We consider now an alternative approach consisting in independent discretizations of noise
and information. The noise is discretized using a voronoi tesselation (Nc cells) and
the control is discretized using vertical strips (Ns strips). As shown in the slides, we
need to solve Ns optimization problems (one problem for each strip), formulated as
follows :
Question 5
- Draw a sample of size 2500 value of (w0,w1) and plot the Voronoi diagram using the
voronoi function.
- Discretize uniformly the interval (−1, 1) to define the vertical strips (use 100 strips
and use function linspace).
- Find a closed form formula for the optimal uk.
- Use the function SquareBV to obtain the pik and compute the optimal value of uk.
- Draw the obtained feedback, that is, u as a piecewise constant function of w0 and
graphically compare it to the optimal feedback defined at §2.
- compute the real cost associated to the obtained feedback.
Note that you can use the macro SquareBV in order to compute the surfaces of the intersections of
the cells of a voronoi tesselation and of a given rectangle.
Solutions
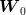 and
and 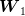 , each with a uniform probability
distribution over
, each with a uniform probability
distribution over ![[− 1,1]](voronoi2x.png) (zero mean, variance
(zero mean, variance 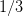 ). The unique decision variable
). The unique decision variable 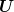 may
only use the observation of
may
only use the observation of 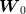 (which we view as the initial state
(which we view as the initial state 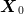 ). The final state
). The final state 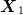 is equal to
is equal to 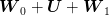 . The goal is to minimize
. The goal is to minimize 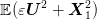 , where
, where  is a given
“small” positive number (“cheap control”). The statement is thus
is a given
“small” positive number (“cheap control”). The statement is thus
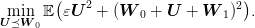
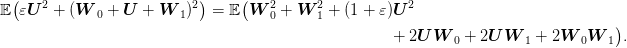
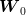 and
and  are centered
independent random variables and since
are centered
independent random variables and since 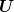 is measurable with respect to
is measurable with respect to 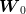 . The first two
terms yield twice the variance
. The first two
terms yield twice the variance 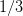 of the noises. Therefore, we remain with the problem of
minimizing
of the noises. Therefore, we remain with the problem of
minimizing

 as a measurable function of
as a measurable function of 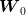 . One can see that the solution is given
by
. One can see that the solution is given
by
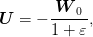
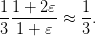

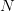 noise trajectories
noise trajectories 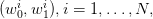 which are
which are 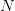 sample of the two-dimensional vector
sample of the two-dimensional vector
 . Those samples will serve to approximate the cost expectation by a usual Monte
Carlo averaging.
. Those samples will serve to approximate the cost expectation by a usual Monte
Carlo averaging.
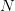 corresponding realizations
corresponding realizations 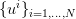 of the random decision variable
of the random decision variable 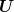 . But we must keep in mind that this random
variable should be measurable with respect to the first component
. But we must keep in mind that this random
variable should be measurable with respect to the first component 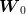 of the previous
vector.
of the previous
vector.
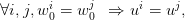
 from taking different values whenever
from taking different values whenever 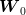 assumes the same value in any
two sample trajectories.
assumes the same value in any
two sample trajectories.
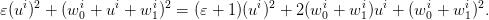
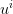 for every
for every 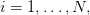 under the constraint (
under the constraint (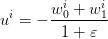
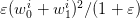 . This is of order
. This is of order  , and so
is the average over
, and so
is the average over 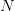 samples
samples
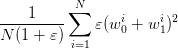
 goes to infinity. This is far from the actual optimal cost given by (
goes to infinity. This is far from the actual optimal cost given by ( such that
such that 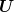 is measurable w.r.t.
is measurable w.r.t.  ) cannot
achieve a cost which is better than the optimal cost (
) cannot
achieve a cost which is better than the optimal cost (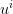 (see (
(see (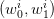 in the square
in the square ![[− 1,1 ]2](voronoi49x.png) . Hence,
before trying to evaluate the cost associated with this “solution”, we must first derive
from it an
. Hence,
before trying to evaluate the cost associated with this “solution”, we must first derive
from it an 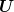 over
over ![Ω = [− 1,1]2](voronoi51x.png) , but with constant value along every vertical line of this square
(since the abscissa represents the first component
, but with constant value along every vertical line of this square
(since the abscissa represents the first component 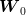 of the 2-dimensional noise
of the 2-dimensional noise
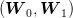 ).
).
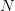 sample points so that the first component
sample points so that the first component 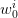 is increasing
with
is increasing
with  ;
;
 vertical strips by drawing vertical lines in the
middle of segments
vertical strips by drawing vertical lines in the
middle of segments ![[wi0,wi0+1]](voronoi58x.png) , that is, the
, that is, the  -th strip is
-th strip is ![[ai−1,ai] × [− 1,1 ]](voronoi60x.png) with
with
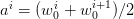 for
for  ,
, 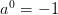 , and
, and 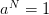 ;
;
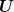 as the function of
as the function of 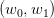 which is piecewise constant
over the square divided into those
which is piecewise constant
over the square divided into those 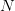 strips, using of course the optimal value
strips, using of course the optimal value 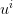 given
by (
given
by ( ; that is, we consider
; that is, we consider
![N
∑ i
U (w ) = u 1[ai−1,ai]×[−1,1](w ),
i=1](voronoi70x.png)
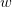 ranges in the square
ranges in the square ![[− 1,1]2](voronoi72x.png) and
and 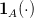 is the function which takes the value 1
in
is the function which takes the value 1
in 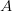 and 0 elsewhere.
and 0 elsewhere.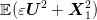 can be evaluated. Here, the expectation is over the argument
can be evaluated. Here, the expectation is over the argument 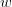 considered as a random variable over the square with uniform distribution (the calculation of this
expectation is done analytically).
considered as a random variable over the square with uniform distribution (the calculation of this
expectation is done analytically).
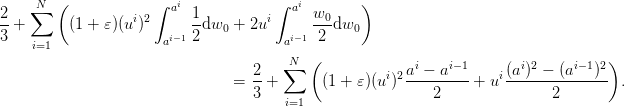
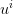
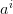
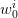
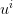
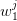
 The question is thus: how to
formulate another constraint translating the informational constraint in the discretized problem
more effective than (
The question is thus: how to
formulate another constraint translating the informational constraint in the discretized problem
more effective than (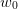 .
.
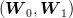 over the square
over the square ![[− 1,1] × [− 1,1]](voronoi86x.png) ), or if they have been recorded from real life
observations, there is a probability
), or if they have been recorded from real life
observations, there is a probability 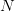 .
.
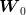 and
and 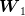 are known to be independent (the white
noise case), any element in a set of
are known to be independent (the white
noise case), any element in a set of 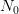 samples of
samples of 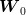 can be combined with the
same, or
can be combined with the
same, or 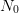 distinct, sets of
distinct, sets of 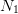 samples of
samples of 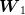 to produce such a tree. Even
if
to produce such a tree. Even
if 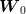 and
and 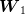 were not independent, one could first generate
were not independent, one could first generate 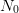 samples of
samples of
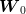 using the marginal probability law of this variable, and then, using each sample
using the marginal probability law of this variable, and then, using each sample
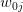 and the
and the 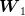 knowing that
knowing that 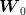 assumes the
value
assumes the
value 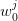 , one could generate
, one could generate 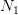 associated samples
associated samples 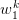 of
of 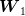 (“sons” of that
(“sons” of that
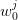 ).
).
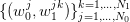 and we introduce the following
additional symbols:
and we introduce the following
additional symbols:
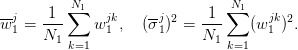
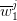 can be interpreted as an estimate of the
can be interpreted as an estimate of the 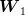 knowing that
knowing that 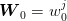 . Likewise,
. Likewise, 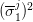 can be interpreted as an estimate of the
can be interpreted as an estimate of the 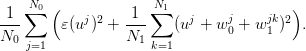
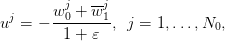
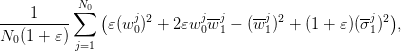
 goes to infinity, then (
goes to infinity, then (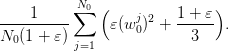
 can also be viewed as an estimate of the second order
moment of
can also be viewed as an estimate of the second order
moment of 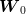 and, if we assume that it converges to the true value 1/3 when
and, if we assume that it converges to the true value 1/3 when 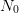 goes to
infinity, then we recover, in the limit, the true optimal cost (
goes to
infinity, then we recover, in the limit, the true optimal cost (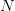 replaced by
replaced by 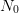 ). Again, we have appealed to a computer
program using 100 experiments, each consisting in:
). Again, we have appealed to a computer
program using 100 experiments, each consisting in: 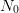 values
values 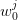 at random;
at random;
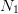 values
values  at random;
at random;
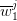 ’s (see (
’s (see (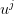 ’s (see (
’s (see (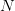 replaced by
replaced by 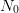 ) with those values after reordering the indices
) with those values after reordering the indices 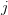 so that
so that 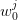 is increasing with
is increasing with 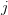 ;
;
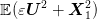 by analytic integration w.r.t. the couple
by analytic integration w.r.t. the couple
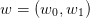 with uniform probability distribution over the square
with uniform probability distribution over the square ![2
[− 1,1]](voronoi136x.png) .
.
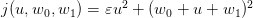
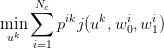
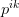 is the probability weight of the intersection of cell
is the probability weight of the intersection of cell  with strip
with strip
 .
.