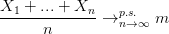
Soit (Xn)n≥1 une suite de variables aléatoires identiquement distribuées, indépendantes et intégrables. Alors les moyennes partielles convergent presque sûrement et en moyenne (dans L1) vers la constante m = 𝔼(X1), soit
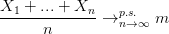
Question 1
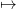
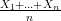 pour n ∈ [1,N].
pour n ∈ [1,N].
Question 2 Reprendre les questions précédentes avec une loi uniforme puis une loi normale à la place d’une loi exponentielle.
Question 3 Reprendre les questions précédentes avec une loi de Cauchy de paramètre a = 1.
Qu’observe-t-on ?
Soit (Xn)n > 1 une suite de variables aléatoires indépendantes identiquement distribuées de carré intégrable. Si m = 𝔼(X1) désigne la moyenne commune des Xn et Sn = ∑ k=1nX k, alors
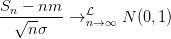
Question 4 Vérifier le théorème de la limite centrale à l’aide d’une procédure Scilab que vous écrirez, et ce pour plusieurs des lois que vues auparavant: loi uniforme, exponentielle...