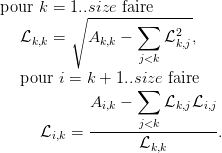+, - addition, soustraction
* ,
 multiplication, puissance (matricielles)
multiplication, puissance (matricielles) .* ,.
 multiplication terme à terme, puissance terme à terme
multiplication terme à terme, puissance terme à terme A\b solution de A*x=b
b/A solution de x*A=b
./ division terme à terme
Scilab (contraction de Scientific Laboratory) est un logiciel libre, développé conjointement par l’INRIA et l’ENPC. Il est téléchargeable gratuitement à partir de
C’est un environnement de calcul numérique qui permet d’effectuer rapidement toutes les résolutions et représentations graphiques couramment rencontrées en mathématiques appliquées.
Scilab (qui ressemble beaucoup à Matlab) est basé sur le principe que tout calcul, programmation ou tracé graphique peut se faire à partir de matrices rectangulaires. En Scilab, tout est matrice : les scalaires sont des matrices, les vecteurs lignes des matrices, les vecteurs colonnes des matrices.
Dans une ligne de commande, tout ce qui suit // est ignoré, ce qui est utile pour les commentaires. Les commandes que nous proposons sur des lignes successives sont supposées être séparées par des retours-chariots.
Ajouter un point virgule en fin de ligne supprime l’affichage du résultat (le calcul est quand même effectué). Ceci évite les longs défilements à l’écran, et s’avère vite indispensable.
Les résultats sont affectés par défaut à la variable ans (“answer”), qui contient donc le résultat du dernier calcul non affecté. Toutes les variables d’une session sont globales et conservées en mémoire. Des erreurs proviennent souvent de confusions avec des noms de variables déjà affectés. Il faut penser à ne pas toujours utiliser les mêmes noms, ou à libérer les variables par clear. Les variables courantes sont accessibles par who et whos.
La commande stacksize permet de connaître la taille de la pile utilisée par Scilab pour stocker les variables. Si cette taille est trop faible, on peut l’ajuster grâce stacksize(n) où n est un entier. Pour plus de détails, faire help stacksize.
L’aide en ligne est appelée par help. La commande apropos permet de retrouver les rubriques d’aide quand on ignore le nom exact d’une fonction.
Toutes les opérations sont matricielles. Tenter une opération entre matrices de tailles non compatibles retournera en général un message d’erreur, sauf si une des matrices est un scalaire. Dans ce cas, l’opération (addition, multiplication, puissance) s’appliquera terme à terme.
Les opérations terme à terme sur les matrices s’effectuent grâce à l’opérateur classique + - et * / ^ précédé d’un point.
En résumé les différentes opérations matricielles sont :
+, - addition, soustraction
* , multiplication, puissance (matricielles)
multiplication, puissance (matricielles)
.* ,. multiplication terme à terme, puissance terme à terme
multiplication terme à terme, puissance terme à terme
A\b solution de A*x=b
b/A solution de x*A=b
./ division terme à terme
Cette brève présentation de Scilab est inspirée des manuels ”Scilab: une introduction” de Jean-Philippe Chancelier et ”Démarrer en Scilab” de Bernard Ycart.
Lire et exécuter les lignes suivantes.
Soit (Y 1,…,Y n) un n-échantillon de variables aléatoires de loi uniforme sur [0, 1]. En regardant
l’aide sur la fonction cumsum (tapez help cumsum), calculez le vecteur = (1,…,n) des
moyennes empiriques où i = 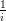 ∑
k=1iY
k et tracez l’évolution de la moyenne empirique i
∑
k=1iY
k et tracez l’évolution de la moyenne empirique i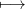 i à
l’aide de la fonction plot2d.
i à
l’aide de la fonction plot2d.
On considère un n-échantillon (Z1,…,Zn) où les variables aléatoires Zi sont i.i.d de même loi que
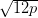
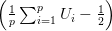 , les variables aléatoires (Ui,i ≤ p) étant i.i.d de loi uniforme sur
[0,1].
, les variables aléatoires (Ui,i ≤ p) étant i.i.d de loi uniforme sur
[0,1].
Utiliser le programme suivant pour tracer l’histogramme à nc classes de (Zi,i ≤ n). Faites varier n, p, nc. Qu’observez-vous pour p = 1, p = 12, nc grand et nc petit? On choisira n de l’ordre de 1000.
On veut simuler des variables aléatoires indépendantes suivant la loi gaussienne centrée réduite 𝒩(0, 1).
 et 𝜃 est
uniformément répartie sur [0, 2π], alors (X,Y ) a pour densité
et 𝜃 est
uniformément répartie sur [0, 2π], alors (X,Y ) a pour densité 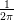 e−
e−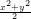 .
.
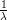 log(U) suit la loi exponentielle
de paramètre λ.
log(U) suit la loi exponentielle
de paramètre λ.
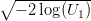 cos(2πU2),
cos(2πU2),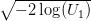 sin(2πU2)) est un couple de
variables aléatoires indépendantes de loi 𝒩(0, 1).
sin(2πU2)) est un couple de
variables aléatoires indépendantes de loi 𝒩(0, 1). On veut maintenant simuler un vecteur gaussien centré de matrice de covariance 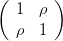 .
Montrer que si
.
Montrer que si 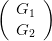 suit la loi 𝒩
suit la loi 𝒩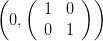 alors
alors
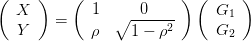
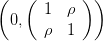 .
.
Remarque. La matrice ℒ = 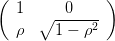 est en fait la décomposition de Cholesky de
M =
est en fait la décomposition de Cholesky de
M = 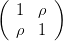 (i.e. ℒℒT = M et ℒ triangulaire inférieure). Cette méthode permet de
simuler un vecteur gaussien dès que l’on a calculé la décomposition de Cholesky de sa
matrice de covariance. Sous Scilab la fonction chol permet de calculer la décomposition de
Cholesky d’une matrice symétrique. Cette fonction renvoie ℒT . Une version de l’algorithme
de Cholesky est proposée en annexe.
(i.e. ℒℒT = M et ℒ triangulaire inférieure). Cette méthode permet de
simuler un vecteur gaussien dès que l’on a calculé la décomposition de Cholesky de sa
matrice de covariance. Sous Scilab la fonction chol permet de calculer la décomposition de
Cholesky d’une matrice symétrique. Cette fonction renvoie ℒT . Une version de l’algorithme
de Cholesky est proposée en annexe.
Utilisez le programme suivant pour simuler un vecteur gaussien centré et faites varier ρ.
On cherche à estimer la densité de la loi d’un échantillon. La première approche est de tracer l’histogramme renormalisé des valeurs obtenues.
Une autre est d’estimer la densité de l’échantillon simulé par la méthode des noyaux décrite ci-après.
Soit f la densité de probabilité à estimer. Soit (X1,...,Xn) un échantillon de la v.a. i.i.d de loi de densité f. La mesure empirique
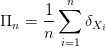
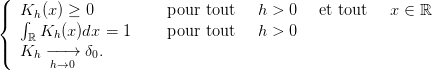
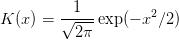
![3- 2
K (x ) = 4(1 − x )I]−1,1[(x).](initiation-proba22x.png)
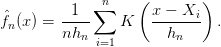
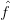 n converge vers f. On admettra qu’un choix judicieux pour la suite (hn)n est de prendre
(hn)n de l’ordre de = n−1∕5.
n converge vers f. On admettra qu’un choix judicieux pour la suite (hn)n est de prendre
(hn)n de l’ordre de = n−1∕5. On considère X et Y deux variables aléatoires gaussiennes centrées, réduites et
indépendantes. On définit une nouvelle variable aléatoire Z telle que Z vaut X avec
probabilité 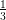 et aY + b avec probabilité
et aY + b avec probabilité 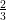 où a > 0 et b ∈ ℝ. Vérifiez que la densité f de Z
s’écrit
où a > 0 et b ∈ ℝ. Vérifiez que la densité f de Z
s’écrit
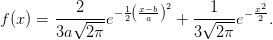
Utilisez le programme suivant pour voir comment évolue l’estimation de la densité en fonction de h. La vraie densité apparaît en rouge sur le graphique.
La méthode de Monte-Carlo permet le calcul de valeurs approchées d’intégrales multiples en utilisant des réalisations i.i.d. de loi uniforme. Si (Xn)n≥1 est une suite de v.a. i.i.d. de loi uniforme sur [0, 1]m et si f : [0, 1]m → ℝ est une fonction mesurable, alors la loi des grands nombres appliquée à la suite de v.a.r. i.i.d. (f(Xn))n≥1 entraîne la convergence presque-sûre suivante :
![1 ∫
--(f(X1 ) + ⋅⋅⋅ + f(Xn )) −→ 𝔼 [f (X1)] = f(x)dx,
n n→+ ∞ [0,1]m](initiation-proba28x.png)
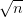 . Cette vitesse est
relativement lente en petite dimension comparée aux méthodes déterministes. En revanche elle
devient très pertinente en dimension élevée. De plus cette méthode ne demande, à priori, aucune
régularité particulière sur f.
. Cette vitesse est
relativement lente en petite dimension comparée aux méthodes déterministes. En revanche elle
devient très pertinente en dimension élevée. De plus cette méthode ne demande, à priori, aucune
régularité particulière sur f.
Vérifiez que les trois intégrales suivantes sont bien égales à π. Utilisez le programme suivant pour comprendre comment approximer la valeur de π. Quelle est selon vous la plus efficace?
![∫ √ -------
4 1 − x2dx
[0,+1]](initiation-proba30x.png)
![∫ ∫
3-
[−1,+1]2 I(x2+y2≤1)dxdy et [−1,+1]34I(x2+y2+z2≤1)dxdydz.](initiation-proba31x.png)
Voici l’algorithme utilisé pour calculer la décomposition de Cholesky ℒ d’une matrice symétrique positive A.