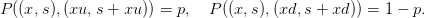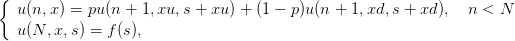Les programmes suivant on été prévu pour être exécutés à l’aide Scicoslab. Ce programme
peut être téléchargé librement sur www.scicoslab.org. Il est disponible sur MacOSX,
Windows ou Linux (Debian, Ubuntu ou Fedora). Noter toutefois qu’il faut installer le server X,
XQuartz sur MacOSX. Ces programmes peuvent aussi fonctionner, moyennant de légère
modification, avec la version officielle de Scilab.
Le fichier source en Scilab correspondant à ce document est accessible. Il est
partiellement mais pas totalement corrigé. Le correction complète sera accessible à la fin du
TD.
1 Un test d’équirépartition
On commence par construire un test d’équirpartition d’une suite de 100 tirages à pile ou
face.
Etude par simulation
On commence par simuler des tirages à pile ou face répétés. On utilise la fonction
scilab, grand avec l’option "bin" (loi binomiale) mais avec un seul tirage (donc loi de
Bernouilli). A partir de ce tirage on calcule le nombre de pile consécutifs maximum dans le
vecteur.
-
1.
- Ecrire une fonction qui génére 100 tirages à pile ou face équilibrés (p = 1∕2, tirages
indépendants) et une fonction qui calcule le nombre maximum de P consécutifs sur ces
tirages.
function X=tirage_pf(n,p)
X=grand(1,n,"bin",1,p); X=string(X);
X=strsubst(X,'0','F');
X=strsubst(X,'1','P'); endfunction
function MAX=max_length(U)
MAX=0;N=0; for n=[1:size(U,'*')] do
MAX=max(MAX,N); end endfunction
-
2.
- On aura besoin de tracer des histogrammes.
function H=histo_discret(samples,maxsize,varargin)
H=0 for k=0:maxsize do
H(k+1)=length(find(samples==k)) ./size(samples,'*'); end; [lhs,rhs]=argn(0);
if (rhs==3) & (varargin(1)==[%t]) then xbasc;plot2d3(0:maxsize,H);
f=gcf(); Dessin=f.children(1).children(1).children(1);
Dessin.thickness=10;Dessin.foreground=5; end; endfunction
-
3.
- Faire 1000 tirages du nombre maximum de P et en tracer un histogramme. On calcule
par simulation une approximation de la loi du nombre maximum de piles consecutifs (un
histogramme d’un grand nombre de tirages i.i.d.).
function main_1() p=1/2;
U=tirage_pf(20,p);
max_length(U);
N=100;X=0;
Taille=1000; for i=[1:Taille] do U=tirage_pf(N,p);
X(i)=max_length(U); end;
plot_flag=%t histo_discret(X,20,plot_flag) endfunction
-
4.
- Montrer que le nombre de piles successifs jusqu’à l’instant courant est une chaîne de
Markov à valeurs dans N de matrice de transition P(x,x + 1) = 1∕2, P(x, 0) = 1∕2.
Simuler et tracer de trajectoires de cette chaîne.
function X=trajectoire(U)
X=0;val=0; for n=[1:prod(size(U))] do
X(n)=val; end endfunction
function main_2() N=100; p=1/2; rectangle=[1,0,N,8];
U=tirage_pf(N,p);
X=trajectoire(U); xbasc;plot2d2(1:N,X,rect = rectangle);
xclick;
for i=1:4 do U=tirage_pf(N);
plot2d2(1:N,trajectoire(U),rect = rectangle,style = i+1);
xclick; end; endfunction;
Calcul exact de la probabilité
On calcule exactement la probabilité de voir au moins l piles consécutifs.
-
1.
- Calculer la matrice de transition de la chaîne arrêté en l, l’implementer en Scicoslab.
En déduire la probabilité d’avoir au moins l pile consécutifs pour l = 0,…, 20.
function Pro=proba(N,l,p)
P=[p*diag(ones(l,1));zeros(1,l-1),1]; P=[[(1-p)*ones(l,1);0],P]; PN=P^N;
endfunction
-
2.
- Calculer la loi du nombre maximum de piles consécutifs.
function loi=calculer_loi(N,p) MAXMAX=30;
previous=1;
for l=0:min(N,MAXMAX) do
loi(l+1)=previous-current;
previous=current; end loi=loi'; endfunction
-
3.
- Comparer avec les simulations précédentes. Vérifier que P(X = 3) est du même ordre
que P(X = 10).
function main_3()
calculer_loi(1,1/2)
calculer_loi(2,1/2) N=100;p=1/2;
loi=calculer_loi(N,p); sum(loi);
xbasc;plot2d3(0:20,loi(1:21)); f=gcf();Dessin=f.children(1).children(1).children(1);
Dessin.thickness=10; Taille=10000;
for i=[1:Taille] do U=tirage_pf(N); X(i)=max_length(U);
end histo=0; for i=0:20 do histo(i+1)=sum(X==i)/Taille;
end histo=histo'; epsilon=norm(histo(1:21)-loi(1:21))
printf("epsilon=%f, petit en principe.\n",epsilon) endfunction
Test du critère
-
1.
- Vérifier que, pour des tirages aléatoires, le test proposé (runs plus grand que 4)
fonctionne dans la plupart des cas (97%).
function main_4()
N=100; p=1/2; Taille=10;
for i=[1:Taille] do U=tirage_pf(N,p); if max_length(U) >= 4 then
printf("OK\n"); else
printf("test négatif\n"); end end; endfunction;
Comment le loi varie t’elle en fonction de N ?
On regarde ce qui se passe lorsque N devient grand.
-
1.
- Calculer le maximum de vraisemblance de la loi du “run maximum” en fonction de N
(N = 100, N = 500, N = 1000).
function main_5()
p=1/2; printf('N: indice du max -> maximum\n');
for N=[10,100,1000] do loi=calculer_loi(N,p);
imax=imax-1; printf('%d: %d -> %f\n',N,imax,m);
end endfunction
-
2.
- Vérifier que la moyenne du “run maximum” varie linéairement en fonction de log(N).
function s=moyenne(loi) N=size(loi,'*')-1;
endfunction
function main_5_bis()
p=1/2; i=0; for N=[10,50,100,500,1000,5000,10000] do
i=i+1; loi=calculer_loi(N,p); x(i)=log(N); y(i)=moyenne(loi);
printf('%d: %f ?=? %f\n',N,y(i),x(i)); end; plot2d(x,y); endfunction
2 Calcul du prix d’une option européenne dans le modèle de Cox-Ross
Simulation du modèle
On considère le chaîne de Cox-Ross :
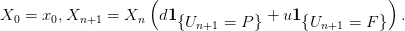
avec N = 10, x0 = 100, p = 1∕2, u = 1 + 1∕N, d = 1 − 1∕N.
On cherche à calculer E(f(XN)) où f(x) = max(x − K, 0) avec K = 100.
-
1.
- Simuler cette chaîne de Markov.
function X=simul_cox_ross(N,x_0,p,u,d)
U=grand(1,N,"bin",1,p);
X=x_0*[1,cumprod(u^U .*d^(1-U))];
endfunction;
function main_6() N=50; sigma=0.3; p=1/2;u=1-sigma/sqrt(N);d=1+sigma/sqrt(N);
x_0=1; X=simul_cox_ross(N,x_0,p,u,d); plot2d2(0:N,X); endfunction
Une version récursive
-
1.
- Ecrire une version récursive de l’algorithme de calcul de prix.
K=100; function res=f(x) res=max(x-K,0); endfunction
function res=prix_recursif(x,k,N) if k==N then res=f(x);return;end;
endfunction
function res=prix_slow(x,N) res=prix_recursif(x,0,N); endfunction
-
2.
- Tester l’algorithme avec N petit (N = 10).
N=10;
sigma=0.3; p=1/2;d=1-sigma/sqrt(N);u=1+sigma/sqrt(N);
prix_slow(100,N);
Une version itérative
-
1.
- Ecrire une version efficace (itérative) de l’algorithme de calcul de prix. Tracer la fonction
x → u(0,x) pour x ∈ [80, 120].
function res=inc(n)
res=n+1; endfunction;
function res=prix(x_0,N) U=zeros(N+1,N+1);
for k=[0:N] do
U(N+1,k+1)=f(x_0*u^k*d^(N-k)); end; for n=[N-1:-1:0] do
end; res=U(1,1); endfunction;
-
2.
- Comparer le résultat des deux versions de l’algorithme.
function main_7() N=10; sigma=0.3; p=1/2;d=1-sigma/sqrt(N);u=1+sigma/sqrt(N);
K=100;x_0=100; prix(x_0,N)
printf('différence entre les 2 resultats: %e\n',abs(prix_slow(x_0,N)-prix(x_0,N)));
endfunction
-
3.
- Que constatez vous lorsque N augmente (N = 10, 100, 200, 500) et que l’on choisit u et d
en fonction de N de la façon suivante :
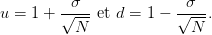
function main_8()
sigma=0.6;
couleur=1 plot2d([50:150],max([50:150]-K,0));
for N=[3,5,10,20,50,100,200] do d=1-sigma/sqrt(N);u=1+sigma/sqrt(N);
n=0; for x=[50:150] do n=n+1; courbe(n)=prix(x,N);
end couleur=couleur+1; plot2d([50:150],courbe,style = couleur);
xclick; end endfunction
Un cas numériquement délicat : les options sur moyenne
On cherche maintenant à évaluer E(f(SN)) où Sn = X1 +  + Xn.
+ Xn.
-
1.
- Pourquoi le processus (Sn,n ≥ 0) n’est il pas une chaîne de Markov ? Vérifier que
le couple ((Xn,Sn),n ≥ 0) est une chaine de Markov de matrice de transition (0
sinon)
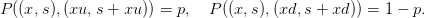
issue de (x0, 0) à l’instant 0. En déduire que E(f(SN)) = u(0,x0, 0) où est la solution
unique de
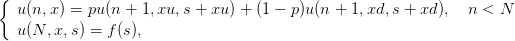 | (1) |
-
2.
- Ecrire un algorithme récursif (lent) qui résoud (1) (N ≤ 10 !) et permet de calculer
E(f(SN)).
function res=f_moy(x,s) res=max((s/N)-K,0);endfunction function res=prix_moyenne(x,s,k,N)
if k==N then res=f_moy(x,s);return;end; endfunction
function res=prix_slow_moyenne(x,N) res=prix_moyenne(x,x,0,N); endfunction
-
3.
- Vérifier (par simulation ou à l’aide de l’algorithme précédent) que les points que peut
atteindre la chaîne (Xn,Sn) sont tous différents et se convaincre qu’il sera (donc) difficile
d’écrire un algorithme exact plus efficace que l’algorithme précédent pour calculer
E(f(SN)).
function main_9() N=10;sigma=0.3; p=1/2;d=1-sigma/sqrt(N);u=1+sigma/sqrt(N);
x_0=100;K=100;
printf('Prix option sur moyenne: %f\n',prix_slow_moyenne(x_0,N)); endfunction
function liste=liste_moyenne_rec(x,s,k,N)
if k==N then
liste=[x;s]; return; end;
endfunction function liste=liste_moyenne(x,N)
liste=liste_moyenne_rec(x,x,0,N) endfunction
function main_10() N=10; x_0=100; sigma=0.3;
p=1/2;d=1-sigma/sqrt(N);u=1+sigma/sqrt(N); liste=liste_moyenne(x_0,N);
[y,p]=sort(liste(2,:));
liste1=liste(:,p);
epsilon=0.001;
Taille=size(liste); match=[]; for i=[1:Taille(2)-1] do
if (norm(liste1(:,i)-liste1(:,i+1)) < epsilon) then
printf("Warning: (%f,%f) ~ (%f,%f)\n",liste1(1,i),liste1(2,i),liste1(1,i+1), ...
liste1(2,i+1));
match=[match,[liste1(1,i),liste1(2,i),liste1(1,i+1),liste1(2,i+1)]]; end; end;
if size(match,'*')==0 then printf("Aucun point n''est dupliqué."); end endfunction
Dans ce cas l’“arbre n’est pas recombinant” et l’on ne peut éviter un algorithme de
complexité 2N. Il faut recourrir à d’autres approximations pour obtenir un algorithme
réaliste (mais approché ...).
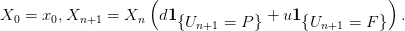
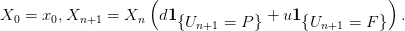
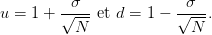
 + Xn.
+ Xn.