Question 8 Le processus des données corrigées de la tendance est XtCT = X
t −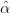 0 −
0 −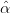 1t,
avec (
1t,
avec (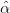 0,
0,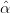 1) qui minimise ∑
t=1T (X
t − α0 − α1t)2. Tracer XCT et commenter.
1) qui minimise ∑
t=1T (X
t − α0 − α1t)2. Tracer XCT et commenter.
Question 1 Simuler une série chronologique Xt = φ1Xt−1 + φ2Xt−2 + φ3Xt−3 + 𝜀t, où les variables aléatoires (𝜀t,t ≥ 0) sont indépendantes de loi gaussienne centrée réduite. On pourra utiliser la fonction ar(X0,X−1,X−2,φ1,φ2,φ3,T) qui simule la série sur l’horizon {0,…,T} défini dans ar.sce.
La commande plot2d(X) permet de tracer le processus X. La commande xbasc() permet de vider le contenu de la fenêtre graphique.
Le polynôme associé au processus AR(p) de coefficient phi= (φ1,…,φp) est donné par la commande p=poly([1-phi],"x","coef"). La commande suivante permet de connaître le module des racines du polynôme p: abs(roots(p)).
Question 2 Qu’observez vous si l’une des racines du polynôme p est de module inférieur à 1? (On pourra simuler un processus AR(1) avec |φ1| > 1.)
Question 3 Effectuer un test de blancheur sur un bruit blanc et sur un processus AR(1). Qu’observez vous? Le justifier. On pourra utiliser la fonction test_blancheur(X) (blanc.sce), où X correspond aux données observées.
Question 4 Pour les séries simulées dans la question précédente, tracer les autocorrélogrammes et le périodogramme. Commentaires. Les fonctions [rho] = autocorel(X) (autocorel.sce) et [omega, f] = periodogramme(X) (period.sce) calculent respectivement la fonction d’autocorrélation et la densité spectrale.
Question 5 Montrer que l’estimation des paramètres d’un processus AR(p) par moindre carré est équivalent à la résolution des équations de Yule-Walker.
Question 6 Simuler un processus AR(p). Estimez les paramètres du processus, en supposant que ces réalisations proviennent d’un processus AR(k). Qu’observez vous si k < p, si k = p et si k > p? On pourra utiliser la fonction [phi]=ar_fit(X, k) définie dans le fichier ar_fit.sce.
On considère un bruit blanc, (𝜀t,t ≥ 1), auquel on rajoute une tendance linéaire, (Tt = α0 + α1t,t ≥ 1), et une saisonalité de période 12, (St = βt mod. 12,t ≥ 1), pour obtenir le processus X = (Xt,t ≥ 1).
La fonction [a, res, s2, V] = reg_lin(X, Y) (reg.sce) renvoie dans a les coefficients de la régression linéaire de X sur Y, dans res les résidus de la régression, dans s2 la variance des résidus et dans V la matrice de covariance des coefficients.
Question 7 Simuler des données issues d’un tel processus avec une tendance linéaire et un période mensuelle, sur une période de 12 ans. On pourra utiliser la fonction X = simul_decomp(alpha0, alpha1, beta, T) du fichier simul_decomp.sce.
Question 8 Le processus des données corrigées de la tendance est XtCT = X
t −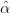 0 −
0 −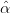 1t,
avec (
1t,
avec (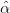 0,
0,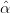 1) qui minimise ∑
t=1T (X
t − α0 − α1t)2. Tracer XCT et commenter.
1) qui minimise ∑
t=1T (X
t − α0 − α1t)2. Tracer XCT et commenter.
Question 9 Le processus des données corrigées des variations saisonnières est XtCV S =
Xt −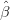 t mod. 12 , où (
t mod. 12 , où (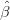 i; 1 ≤ i ≤ 12) réalise le minimum de
i; 1 ≤ i ≤ 12) réalise le minimum de
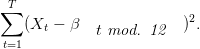
Donner les intervalles de confiance sur les paramètre (β1,…,β12). Tracer XCV S et commenter.
Question 10 Estime les paramètres (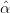 1,
1,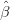 1,…,
1,…,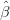 12) en minisant
12) en minisant
![T
∑ 2
(Xt − α0 − α1t − βt[12]) .
t=1](serie-chrono10x.png)
On fournira également un intervalle de confiance pour les paramètres estimés.
On dispose du nombre mensuel de passagers sur les vols internationaux de janvier 1949 à décembre 1960: Z = (Zt, 1 ≤ t ≤ T) avec T = 144.
Question 11 Tracer les données, Z, avec plot2d. Tracer l’évolution de la moyenne annuelle et de la moyenne annuelle de (log(Zt), 1 ≤ t ≤ T). Tracer le périodogramme pour Z et log(Z). Que remarquez vous?
On pose Xt = log(Zt).
Question 12 Estimer la tendance et les variations saisonnières de X. Les résidus, forment-ils un bruit blanc?
Question 13 Tracer les autocorrélogrammes des résidus.
On considère le processus différencié U = (Ut,t ≥ 2) où Ut = Xt − Xt−1 et le processus W = (Wt,t ≥ 14) avec Wt = Ut − Ut−12.
Question 14 Quel est l’intérêt du processus U par rapport à une tendance? Quel est l’intérêt du processus W par rapport à une variation saisonnière annuelle?
Question 15 Tracer les processus X,U et W ainsi que leurs autocorrélogrammes simple et partiel. On pourra réutiliser la fonction plot2d(autocorel(X)) pour tracer l’autocorrélogramme simple. La fonction a=autocorel_part(X) (autocorel_part.sce) permet de calculer l’autocorrélogramme partiel.
Question 16 Effectuer un test de blancheur sur W. Conclusion.
Question 17 Modéliser le processus W par un processus AR(12). Effectuer un test de blancheur sur les résidus. Qu’observez vous sur les coefficients estimés? On pourra utliser la fonction res = residu_ar(W, phi) (ar_residu.sce) pour calculer le vecteur des résidus.
Question 18 Modéliser le processus W par Wt = φ1Wt−1 + φ12Wt−12 + 𝜀t. Effectuer un test de blancheur sur les résidus. Conclusion? On pourra utliser la fonction [phi] = sparse_fit(W) (model_W.sce) pour calculer le vecteur ϕ = (ϕ1,ϕ12).
On suppose que l’on observe les données de 1949 à 1959. On veut vérifier le caractère prédictif des modèles.
Question 19 Estimer les paramètres pour les modèles développés dans les deux paragraphes précédents. En déduire deux jeux de prévisions sur le processus Z pour l’année 1960, et les comparer avec les données observées.