Modelo de competencia para hembras Aedes agypti introduciendo Wolbachia

Contents

1 Establecimiento de la infección con Wolbachia entre las hembras silvestres del Aedes aegypti

En este caso se presenta un modelo bidimensional que describe la dinámica poblacional de las hembras del mosquito Aedes aegypti (infectados y no infectados con Wolbachia) que actúan como principales transmisores de diferentes infecciones arbovirales. Este modelo cuenta con la dependencia de densidad y la competencia entre hembras infectadas y no infectadas por los mismos recursos (tales como comida, criaderos, etc). Además, se introduce un termino (llamado término de descompensación critica) que pueda expresar matemáticamente el hecho de que en altas frecuencias de infección por Wolbachia las hembras silvestres (a pesar de tener una mejor aptitud biológica individual) tienen menos posibilidades de producir descendencia viable que las hembras infectadas con Wolbachia.

1.1 Formulación del modelo de competencia

Sea M(t) el número total de hembras del Aedes aegypti presentes en la localidad objetivo en el día t. Se supone que la población de hembras del Aedes aegypti consiste en dos grupos, es decir, M(t) = W(t) + F(t), donde W(t) denota las hembras infectadas con Wolbachia y F(t) denota las hembras silvestres (o no infectadas con Wolbachia). Ambos grupos deben competir por los mismos criaderos y otros recursos disponibles en la localidad objetivo, así como por oportunidades de apareamiento.

Tomando como base el modelo de competencia descrito por Britton(20012) y añadiendo la propiedad inducida por el fenotipo reproductivo de IC, se propone el siguiente modelo para la dinámica poblacional y la iteración de hembras del Aedes aegypti infectadas y no infectadas con Wolbachia:

Aquí, el parámetro Ψ hace referencia a la tasa de nacimientos, r a la tasa de crecimiento intrínseca y δ a la tasa de mortalidad, donde □_f se refiere a las hembras silvestres o no infectadas con Wolbachia y □_w se refiere a las hembras infectadas con Wolbachia. Sin embargo, los significados de K_f,K₀ y K_w merecen más explicaciones. Primero, la ecuación (1a) tiene un comportamiento “casi” logístico, en ausencia de portadores de Wolbachia (es decir, para W(t) = 0). En este caso, el modelo se puede considerar realista solo cuando K₀ → 0. Sin embargo, nuestro interés consiste en modelar la interacción (competencia) de dos especies de mosquitos; por lo tanto, la presencia de hembras con Wolbachia en el sistema dinámico (1) es obligatoria y no puede ser ignorada. Los términos dentro de los corchetes en (1) se refieren exáctamente a la competencia entre hembras infectadas con Wolbachia y las hembras silvestres por los mismos recursos. Esto está en concordancia con los modelos tradicionales de competencia (véase por ejemplo Briton(2012) o textos similares).

La dínamica descrita en (1) se puede trabajar en Scicoslab con el siguiente codigo:

El umbral de población mínima viable para los nativos (PMV) K_♭ puede estimarse a partir de los otros parámetros (en efecto, K_♭ ≥ K₀). De acuerdo con la ecuación (1a), el crecimiento instantáneo de hembras silvestres debe ser negativo 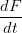< 0 cuando F(t) < K_♭ y positivo 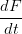> 0 cuando F(t) > K_♭.

También debe observarse que K_f > 0 y K_w > 0 en (1a) son parámetros relacionado con la capacidad de carga de los mosquitos

Numéricamente determine las capacidades de carga de los mosquitos usando el siguiente código Scicoslab:

Numéricamente determine el umbral cambiando los valores iniciales usando el código Scicoslab dado en la pregunta anterior

Para visualizar el campo vectorial y algunas trayectorias de este modelo use el siguiente código Scicoslab: