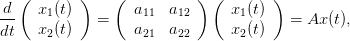
Un système dynamique linéaire plan est de la forme
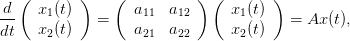 | (1) |
où A est une matrice 2 × 2 non nulle à coefficients réels. On notera λ1 et λ2 ses valeurs propres (éventuellement complexes conjuguées). Plusieurs cas sont à considérer.
Question 1 Charger la fonction syslin suivante sous Scilab. Interpréter ce que calcule cette fonction.
D’un point de vue algébrique, la matrice A admet deux vecteurs propres réels distincts v1 et v2. Si
P = 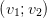 est la matrice réelle de changement de base, on a A = PDiag(λ1,λ2)P−1. Si on
effectue alors le changement de coordonnées z = P−1x, le système (1) devient ż = Diag(λ
1,λ2)z et
les solutions s’écrivent :
est la matrice réelle de changement de base, on a A = PDiag(λ1,λ2)P−1. Si on
effectue alors le changement de coordonnées z = P−1x, le système (1) devient ż = Diag(λ
1,λ2)z et
les solutions s’écrivent :
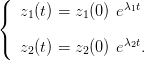 | (2) |
On dit que l’origine est un nœud stable ou instable suivant que λ1 et λ2 sont négatives ou positives. La figure 1 représente un nœud stable. Pour avoir un nœud instable il suffit de changer le sens des flèches.
Question 2 Exécuter syslin(A) sous Scilab. Commenter.
Les solutions sont toujours de la forme (2) mais comme les valeurs propres sont de signe opposé, les trajectoires sont rentrantes dans une direction et sortantes dans l’autre. On dit que l’origine est un point-selle ou encore point-col. La figure 2 représente un point-selle pour lequel λ1 est négative et λ2 positive.
Question 3 Exécuter syslin(A) sous Scilab. Commenter.
Notons les valeurs propres
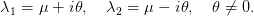
D’un point de vue algébrique, la matrice A admet deux vecteurs propres complexes conjugués
distincts v1 et v2. Si P = 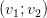 est la matrice complexe de changement de base, on a
A = PDiag(λ1,λ2)P−1. Si on effectue alors le changement de coordonnées complexes
z = P−1x, le système (1) devient ż = Diag(λ
1,λ2)z. Le point complexe z1(t) décrit la
courbe
est la matrice complexe de changement de base, on a
A = PDiag(λ1,λ2)P−1. Si on effectue alors le changement de coordonnées complexes
z = P−1x, le système (1) devient ż = Diag(λ
1,λ2)z. Le point complexe z1(t) décrit la
courbe
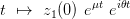 | (3) |
qui est une spirale autour de l’origine. Celle ci est dite spirale instable, centre ou spirale stable suivant que μ est positif, nul ou négatif comme l’indique la figure 3.
Question 4 Exécuter syslin(A) sous Scilab. Commenter.
Question 5 Même question avec la matrice de rotation suivante.
Les solutions sont de la même forme que (2) mais comme λ1 et λ2 sont égales, le rapport z1(t)∕z2(t) reste constant égal à z1(0)∕z2(0) et les trajectoires sont des droites. On dit que l’origine est un foyer stable ou instable suivant que λ1 est négative ou positive. La figure 4 représente un foyer instable.
Question 6 Exécuter syslin(A) sous Scilab. Commenter.
Il existe une matrice réelle de changement de base P telle que, d’après la réduction de Jordan,
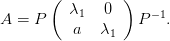 | (4) |
Si on effectue le changement de coordonnées z = P−1x, le système (1) devient ż = 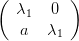 z
et les solutions s’écrivent :
z
et les solutions s’écrivent :
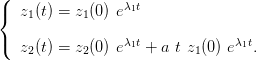 | (5) |
On dit que l’origine est un nœud dégénéré stable ou instable suivant que λ1 est négative ou positive. La figure 5 représente un nœud dégénéré stable.
Question 7 Exécuter syslin(A) sous Scilab. Commenter.
La matrice A étant supposée non nulle, on étudie le cas où λ1 = 0 et λ2 = λ≠0.
D’un point de vue algébrique, la matrice A admet deux vecteurs propres réels distincts v1 et v2.
Si P = 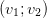 est la matrice réelle de changement de base, on a A = PDiag(0,λ)P−1. Si on
effectue alors le changement de coordonnées z = P−1x, le système (1) devient ż = Diag(0,λ)z et
les solutions s’écrivent :
est la matrice réelle de changement de base, on a A = PDiag(0,λ)P−1. Si on
effectue alors le changement de coordonnées z = P−1x, le système (1) devient ż = Diag(0,λ)z et
les solutions s’écrivent :
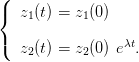 | (6) |
Ainsi, non seulement l’origine, mais aussi tous les points de la droite d’équation z2 = 0 sont points d’équilibre (cas dégénéré).
Question 8 Exécuter syslin(A) sous Scilab. Commenter.
Partant du système linéaire précédent, on ajoute une perturbation quadratique
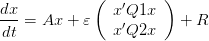 | (7) |
où 𝜀 est un réel, Q1, Q2 des matrices carrées symétriques et R est un vecteur de même dimension que x.
Question 9 Reprendre le code syslin pour en faire un code syslinpert.