Simulation of dynamical systems in discrete time
Ecological and environmental examples

Luc Doyen
(last modification date: October 10, 2017)
Version pdf de ce document
Version sans bandeaux

1 Population dynamics in ecology
2 Carbon cycle
3 An ecosystem

Contents

1 Population dynamics in ecology
2 Carbon cycle
3 An ecosystem

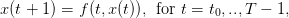
We consider the discrete time dynamics system in ℝn:

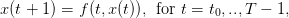x(t + 1) = f (t,x (t)), for t = t0,..,T − 1,
(1)

starting from initial state x0 ∈ ℝn at time t 0

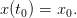x (t0) = x0.
(2)

Knowing function f and (t0,x0), we are able to compute the whole sequence x(t0),x(t0 + 1),…,x(T) solution of the problem.

1 Population dynamics in ecology

Consider the population dynamics

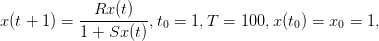
--Rx-(t)-- x (t + 1) = 1 + Sx (t),t0 = 1,T = 100, x(t0) = x0 = 1,

with parameters R = 1.2 and S = 0.02.

  t0=1;x0=1;
  x(t0)=x0;T=100;R=1.2;S=0.02;
  
  function y=f(t,x)
    y=R*x ./(1+S*x)
  endfunction
  
  for t=t0:1:T do
    x(t+1)=f(t,x(t));
  end;
  plot2d(t0:T+1,x(t0:T+1))

Question 1 Change the population dynamics with f(t,x) = (ax)0.5 where a = 10. Compare the behavior of the solutions x(t).

2 Carbon cycle

Consider the carbon cycle

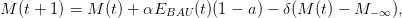
M (t + 1) = M (t) + αEBAU (t)(1 − a) − δ(M (t) − M −∞ ),

starting from initial conditions M0 = 354 (ppm) at year t0 = 1990 with time horizon T = 100. The parameters are α = 0.471, preindustrial concentration M−∞ = 280, removal rate δ = 0.01. It is assumed that the ”business as usual” CO2 emissions path is

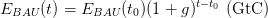
E (t) = E (t )(1 + g)t−t0 (GtC ) BAU BAU 0
with the emissions growth set to g = 1% and initial emissions to EBAU(1990) = 7.2 (GtC).

  t0=1990;T=2100;M_0=354;
  alpha=0.471;M_infty=280;delta=1/120;sigma=0.519;
  E_BAU=7.2;g=0.01
  a=0;
  
  function y=EBAU(t)
    y=E_BAU*(1+g)^(t-t0);
  endfunction
  
  function y=f(t,M)
    y=M+alpha*EBAU(t)*(1-a)-delta*(M-M_infty);
  endfunction
  
  x(t0)=M_0;
  for t=t0:1:T do
    x(t+1)=f(t,x(t));
  end;
  plot2d(t0:T+1,x(t0:T+1),rect = [t0,0,T+1,1000])

Question 2 Change the mitigation rate a (a ∈ [0, 1]) to compare the behavior of the concentrations profile M(t).

3 An ecosystem

We consider two populations x1(t),x2(t) interacting within a trophic web. The dynamics based on a Lotka-Volterra form is characterized by

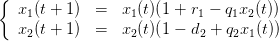{ x1(t + 1) = x1 (t)(1 + r1 − q1x2 (t)) x2(t + 1) = x2 (t)(1 − d2 + q2x1(t))
(3)

where r1 > 0 is the intrinsic growth of prey while d2 > 0 is the intrinsic decrease of predator. Parameters q1 > 0,q2 > 0 are related to the catchability and efficiency of trophic relations.

  t0=1;x0=[1;1];
  T=100;
  r_1=0.1;d_2=0.1;q_1=0.1;q_2=0.2;
  
  function y=f(t,x)
    x_1=x(1);x_2=x(2);
    y_1=x_1 .*(1+r_1-q_1*x_2);
    y_2=x_2 .*(1-d_2+q_2*x_1);
    y=[y_1;y_2];
  endfunction
  
  x=zeros(2,T+1);
  x(:,t0)=x0;
  for t=t0:1:T do
    x(:,t+1)=f(t,x(:,t));
  end;
  plot2d(t0:T+1,x(:,t0:T+1)')

Question 3 Change parameters r,d or q to compare the behavior of the populations (x1(t),x2(t)).